Capítulo 45 Tamanho da amostra

45.1 Tamanho da amostra

45.1.1 O que é tamanho da amostra?

Tamanho da amostra $n$ é a quantidade de participantes (ou unidades de análise) necessárias para conduzir um estudo a fim de testar uma hipótese.³⁵⁷
O cálculo do tamanho da amostra depende de quatro pilares interligados — tamanho de efeito esperado, variabilidade, nível de significância ($\alpha$) e poder ($1-\beta$) — cuja combinação determina o $n$ necessário para detectar efeitos de interesse com precisão adequada.¹⁵

45.1.2 Por que determinar o tamanho da amostra é importante?

É virtualmente impossível, devido a limitações de recursos — tempo, acesso, custo, dentre outros — coletar dados da população completa.⁸
Uma amostra muito pequena para o estudo pode resultar em ajuste exagerado, imprecisão e baixo poder do teste.¹³⁶

45.1.3 Quais fatores devem ser considerados para determinar o tamanho da amostra?

Tamanho da população ($N$): O tamanho da amostra depende parcialmente do tamanho da população de origem. Geralmente assume-se que a população tem tamanho desconhecido ou infinito. Em alguns estudos serão amostradas populações de tamanho finito (inferior a 100.000 indivíduos), geralmente em pesquisas descritivas, em que esse tamanho deve ser incorporado nos cálculos.³⁵⁷
Delineamento do estudo.³⁵⁷
Quantidade e características (dependente vs. independente) dos grupos de participantes do estudo.³⁵⁷
Erros tipo I ($\alpha$) e tipo II ($\beta$).³⁵⁷
Tipo de variável a ser observada (contínua, intervalo, ordinal, nominal, dicotômica).³⁵⁷
Tamanho de efeito mínimo a ser observado.³⁵⁷
Variabilidade da(s) variável(eis) coletada(s).³⁵⁷
Lateralidade do teste de hipótese (uni- ou bicaudais).³⁵⁷
Perdas de dados durante a coleta e/ou acompanhamento dos participantes do estudo.³⁵⁷

O pacote pwr²⁸⁴ fornece a função plot.power.htest para apresentar graficamente a relação entre o tamanho da amostra e o poder de testes de hipóteses.

45.1.4 Quais aspectos éticos estão envolvidos no tamanho da amostra?

Determinar a priori o tamanho da amostra pode diminuir o risco de realizar testes ou intervenções desnecessários, de desperdício de recursos (tempo e dinheiro) associados e, por outro lado, de coletar dados insuficientes para testar as hipóteses do estudo.³⁵⁷
O tratamento ético dos participantes do estudo, portanto, não exige que se considere se o poder do estudo é inferior à meta convencional de 80% ou 90%.³⁵⁸
Estudos com poder <80% não são necessariamente antiéticos.³⁵⁸
Metas convencionais de poder (80–90%) são guias pragmáticos e não regras morais rígidas; estudos com poder <80% não são automaticamente antiéticos quando bem justificados.³⁵⁸
Grandes estudos podem ser desejáveis por outras razões que não as éticas.³⁵⁸

45.2 Saturação em pesquisas qualitativas

45.2.1 O que é saturação de dados em pesquisas qualitativas?

Saturação é o ponto em que a coleta de dados não produz novas informações, categorias ou temas, indicando que o fenômeno investigado já foi suficientemente explorado.³⁵⁹
Essa noção surgiu na teoria fundamentada com o termo “saturação teórica”, mas hoje é amplamente usada em diferentes tradições qualitativas, incluindo fenomenologia, etnografia e análise temática.³⁶⁰

45.2.2 Quais tipos de saturação existem?

Saturação de códigos: ocorre quando não emergem novos códigos relevantes nos dados³⁶⁰
Saturação de significados: atinge-se quando a profundidade e a variação dos significados de um tema foram plenamente exploradas.³⁶⁰
Saturação teórica: quando categorias estão suficientemente desenvolvidas e suas relações esclarecidas.³⁵⁹
Saturação de metatemas: em pesquisas multicêntricas, quando os grandes temas transversais já foram identificados.³⁶¹

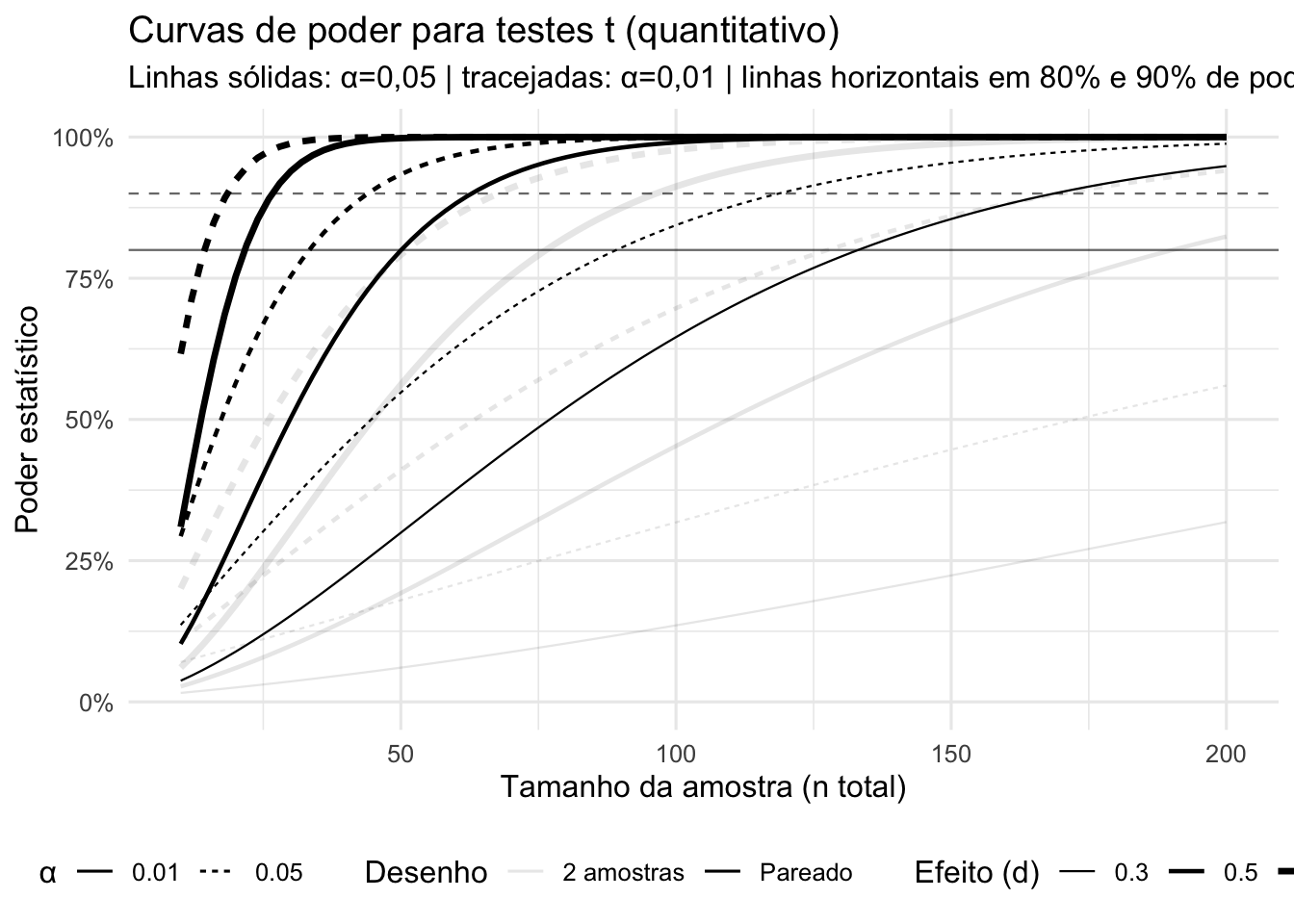
$Curvas de poder para testes t (quantitativo). Linhas sólidas: $\alpha = 0,05$ | tracejadas: $\alpha = 0,01$ | linhas horizontais em 80\% e 90\% de poder.$

Figura 45.1: Curvas de poder para testes t (quantitativo). Linhas sólidas: $\alpha = 0,05$ | tracejadas: $\alpha = 0,01$ | linhas horizontais em 80% e 90% de poder.

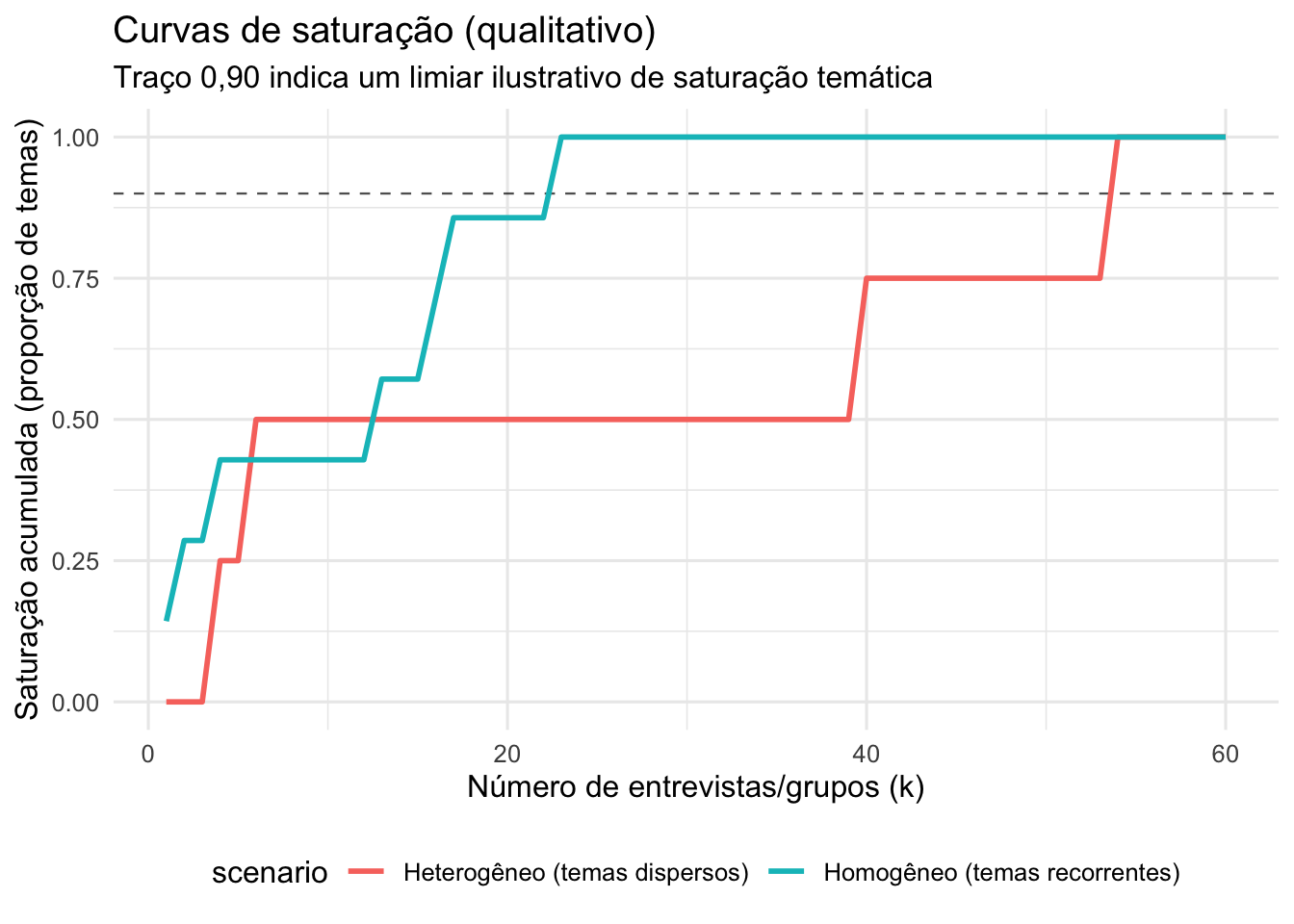
Figura 45.2: Curvas de saturação para estudos qualitativos de descoberta de temas.

45.2.3 Quantas entrevistas ou grupos focais são necessários para alcançar saturação?

Estudos empíricos mostram que a saturação de códigos pode ser atingida com 9 a 17 entrevistas em populações homogêneas e objetivos específicos.³⁶⁰
Para saturação de significados, podem ser necessárias entre 16 e 24 entrevistas.³⁶⁰
Em grupos focais, a saturação temática pode ocorrer com 4 a 8 grupos homogêneos.³⁶⁰
Revisões recentes sugerem que a saturação teórica exige 20 a 30 entrevistas ou mais, dependendo da complexidade do estudo.³⁶¹

45.2.4 Quais debates existem sobre o conceito de saturação?

Defensores argumentam que a saturação é central para garantir rigor e confiança nos resultados qualitativos.³⁵⁹
Críticos sugerem que o conceito pode ser usado de forma rígida, levando a coletas excessivas ou pouco sensíveis a perspectivas únicas.³⁵⁹
Pesquisadores contemporâneos recomendam usar a saturação de forma flexível, adaptada ao contexto, método e população estudada.³⁶¹

45.2.5 Quais recomendações práticas para tamanho de amostras de estudos qualitativos?

Para entrevistas individuais: 9–12 entrevistas podem ser suficientes para saturação temática em contextos homogêneos, mas estudos heterogêneos ou multicêntricos exigem mais casos.^360,361
Para grupos focais: 4–8 grupos são geralmente adequados.³⁶⁰
Para estudos multicêntricos: recomenda-se 20–40 entrevistas por local para alcançar saturação de metatemas.³⁶¹
É importante relatar não apenas o número de entrevistas, mas também como e quando a saturação foi avaliada.³⁶²

45.3 “Fome de dados”

45.3.1 O que significa “fome de dados”?

Data hungry descreve a necessidade de um modelo contar com muitos eventos por variável (EPV) para alcançar estabilidade estatística.
Enquanto a regressão logística (LR) atinge desempenho estável com cerca de 20–50 EPV, modelos como random forest (RF), redes neurais (NN) e máquinas de vetor de suporte (SVM) podem demandar >200 EPV para reduzir o otimismo e estabilizar a AUC.

45.3.2 Por que a “fome de dados” é relevante?

Em bases de dados pequenas, modelos clássicos tendem a ser mais robustos e menos suscetíveis a superajuste.³²⁷
O uso de modelos modernos só se justifica quando há grandes bases de dados, caso contrário o ganho em acurácia é marginal.³²⁷
Esse conceito conecta diretamente a escolha do modelo ao planejamento amostral.³²⁷

45.4 Eventos por variável (EPV) em modelos preditivos

45.4.1 Quantos eventos por variável (EPV) são necessários?

Regressão logística: entre 20 e 50 EPV.³²⁷
Árvore de decisão para classificação e regressão: cerca de 60 EPV.³²⁷
Máquina de vetores de suporte, redes neurais e random forests: muitas vezes >200 EPV e ainda instáveis.³²⁷

45.4.2 O que acontece se não houver eventos suficientes?

Modelos modernos podem apresentar alto otimismo (desempenho inflado no treino, mas ruim na validação).³²⁷
Pequenos bancos de dados favorecem o uso de modelos clássicos.³²⁷

45.5 Cálculo do tamanho da amostra

45.5.1 Como calcular o tamanho da amostra?

O tamanho amostral pode ser calculado por meio de fórmulas matemáticas que tendem a assegurar margens de erros tipos I ($\alpha$) e II ($\beta$) para a estimação dos parâmetros populacionais (tamanho de efeito) a partir dos dados amostrais.³⁵⁷
O tamanho da amostra deve ser calculado para cada um dos objetivos primários e/ou secundários, sendo escolhido o maior tamanho de amostra calculado para o estudo.³⁵⁷
Geralmente é recomendado ser cético em relação às regras práticas para o tamanho da amostra, tais como a proporção entre o número de variáveis (ou eventos) e de participantes.¹³⁶

45.5.2 Como especificar o tamanho do efeito esperado?

Estudo-piloto — realizados nas mesmas condições do estudo, mas envolvendo um tamanho de amostra limitado — pode ser útil na estimativa do tamanho da amostra a partir do tamanho do efeito estimado.³⁵⁷
Utilizar os limites dos intervalos de confiança de estudos-piloto de ensaios clínicos como estimativa do tamanho do efeito pode aumentar o poder estatístico da análise se comparado ao uso das estimativas pontuais obtidas no mesmo piloto.³⁶³
Embora os testes de hipótese considerem efeito nulo para a hipótese nula — ex.: diferença de média ($H_{0}: \mu_{1} - \mu_{2}=0$), correlação ($H_{0}: r=0$), associação ($H_{0}: \beta=0$ ou $H_{0}: OR=1$) —, em geral é improvável que os efeitos populacionais sejam de fato nulos (isto é, exatamente 0).³⁶⁴

O pacote pwr²⁸⁴ fornece a função pwr.2p.test para cálculo do tamanho da amostra para testes de proporção balanceados (2 amostras com mesmo número de participantes).

O pacote pwr²⁸⁴ fornece a função pwr.2p2n.test para cálculo do tamanho da amostra para testes de proporção não balanceados (2 amostras com diferente número de participantes).

O pacote pwr²⁸⁴ fornece a função pwr.anova.test para cálculo do tamanho da amostra para testes de análise de variância balanceados (3 ou mais amostras com mesmo número de participantes).

O pacote pwr²⁸⁴ fornece a função pwr.chisq.test para cálculo do tamanho da amostra para testes de qui-quadrado $\chi^2$.

O pacote pwr²⁸⁴ fornece a função pwr.f2.test para cálculo do tamanho da amostra para testes com modelo linear geral.

O pacote pwr²⁸⁴ fornece a função pwr.norm.test para cálculo do tamanho da amostra para a média de uma distribuição normal com variância conhecida.

O pacote pwr²⁸⁴ fornece a função pwr.p.test para cálculo do tamanho da amostra para testes de proporção (1 amostra).

O pacote pwr²⁸⁴ fornece a função pwr.r.test para cálculo do tamanho da amostra para testes de correlação (1 amostra).

O pacote pwr²⁸⁴ fornece a função pwr.t.test para cálculo do tamanho da amostra para testes t de diferença de 1 amostra, 2 amostras dependentes ou 2 amostras independentes (grupos balanceados).

O pacote pwr²⁸⁴ fornece a função pwr.t2n.test para cálculo do tamanho da amostra para testes t de diferença de 2 amostras independentes (grupos não balanceados).

O pacote longpower³⁵⁵ fornece a função power.mmrm para calcular o tamanho da amostra para estudos com análises por modelo de regressão linear misto.

45.6 Perdas de amostra

45.6.1 O que é perda de amostra?

Perda de amostra(s) — isto é, participante(s) ou unidade(s) de análise — pode ocorrer durante a coleta e/ou acompanhamento dos participantes do estudo.³⁵⁷
Perda amostral pode ocorrer por: abandono ou desistência do participante, perda de contato com o participante, perda de informação, ocorrência de eventos adversos, morte do participante, entre outros.³⁵⁷

45.6.2 Por que a perda de amostra é um problema?

A perda de amostra reduz o tamanho efetivo de $n$ e, portanto, o poder estatístico do estudo, elevando a probabilidade de erro tipo II ($\beta$).^136,357
A atrição diferencial também pode introduzir viés de seleção (ou de atrito), quando as características dos participantes que permanecem diferem sistematicamente das daqueles que se perdem ao seguimento.³⁵⁷

45.6.3 Como evitar perda de amostra?

A perda de amostra pode ser evitada por meio de um planejamento cuidadoso do estudo, incluindo a definição de critérios de inclusão e exclusão claros e apropriados, bem como a definição de estratégias para minimizar a perda de amostra.^REF?
A perda de amostra pode ser compensada pelo aumento do tamanho da amostra, desde que o aumento seja suficiente para manter o poder do estudo.³⁵⁷

45.7 Ajustes no tamanho da amostra

45.7.1 Por que ajustar o tamanho da amostra?

O tamanho da amostra pode ser ajustado durante o estudo para compensar a perda de amostra, desde que o aumento seja suficiente para manter o poder do estudo.³⁵⁷

45.7.2 Como ajustar para perda amostral?

Aumentar o tamanho da amostra estimada $n$ pela porcentagem $d$ de perdas esperada ou prevista, para obter o tamanho da amostra efetiva $n'$ (45.1):³⁵⁷

\[\begin{equation} \tag{45.1} n' = \dfrac{n}{1-d} \end{equation}\]

45.8 Justificativa do tamanho da amostra

45.8.1 Como justificar o tamanho da amostra de um estudo?

Em estudos que envolvem condições raras, pode ser difícil recrutar o número necessário de participantes devido à limitada disponibilidade de casos da população. Mesmo assim, é aconselhável determinar o tamanho da amostra.³⁵⁷
Quando um estudo deste tipo não é possível, as considerações referentes ao tamanho da amostra são justificadas de acordo com o número máximo de pacientes que podem ser recrutados no decorrer do estudo.³⁵⁷

45.8.2 Como justificar o tamanho da amostra em estudos qualitativos?

Pesquisas qualitativas devem apresentar uma justificativa explícita da amostra, relacionando-a à estratégia de coleta, aos objetivos e ao critério de saturação adotado.³⁶²
A noção de “poder da informação” (information power) indica que quanto mais relevante e focada é a amostra em relação à pergunta de pesquisa, menor pode ser o número de participantes.³⁶²
Relatar claramente o processo de decisão aumenta a transparência e a credibilidade da pesquisa.³⁶²

Citar como:
Ferreira, Arthur de Sá. Ciência com R: Perguntas e respostas para pesquisadores e analistas de dados. Rio de Janeiro: 1a edição,

Referências

Kwak SG, Kim JH. Central limit theorem: the cornerstone of modern statistics. Korean Journal of Anesthesiology. 2017;70(2):144. doi:10.4097/kjae.2017.70.2.144

15.

Banerjee A, Chaudhury S. Statistics without tears: Populations and samples. Industrial Psychiatry Journal. 2010;19(1):60. doi:10.4103/0972-6748.77642

136.

Smeden M van. A Very Short List of Common Pitfalls in Research Design, Data Analysis, and Reporting. PRiMER. 2022;6. doi:10.22454/PRiMER.2022.511416

284.

Champely S. pwr: Basic Functions for Power Analysis.; 2020. https://CRAN.R-project.org/package=pwr.

327.

Ploeg T van der, Austin PC, Steyerberg EW. Modern modelling techniques are data hungry: a simulation study for predicting dichotomous endpoints. BMC Medical Research Methodology. 2014;14(1). doi:10.1186/1471-2288-14-137

355.

Iddi S, Donohue MC. Power and Sample Size for Longitudinal Models in R – The longpower Package and Shiny App. The R Journal. 2022;14:264–282.

358.

Bacchetti P. Ethics and Sample Size. American Journal of Epidemiology. 2005;161(2):105–110. doi:10.1093/aje/kwi014

359.

Ahmed SK. Sample size for saturation in qualitative research: Debates, definitions, and strategies. Journal of Medicine, Surgery, and Public Health. 2025;5:100171. doi:10.1016/j.glmedi.2024.100171

360.

Hennink M, Kaiser BN. Sample sizes for saturation in qualitative research: A systematic review of empirical tests. Social Science & Medicine. 2022;292:114523. doi:10.1016/j.socscimed.2021.114523

361.

Wutich A, Beresford M, Bernard HR. Sample Sizes for 10 Types of Qualitative Data Analysis: An Integrative Review, Empirical Guidance, and Next Steps. International Journal of Qualitative Methods. 2024;23. doi:10.1177/16094069241296206

362.

Vasileiou K, Barnett J, Thorpe S, Young T. Characterising and justifying sample size sufficiency in interview-based studies: systematic analysis of qualitative health research over a 15-year period. BMC Medical Research Methodology. 2018;18(1). doi:10.1186/s12874-018-0594-7

363.

Ying X, Robinson KA, Ehrhardt S. Re-evaluating the role of pilot trials in informing effect and sample size estimates for full-scale trials: a meta-epidemiological study. BMJ Evidence-Based Medicine. 2023;28(6):383–391. doi:10.1136/bmjebm-2023-112358

364.

Andrade C. Sample Size and its Importance in Research. Indian Journal of Psychological Medicine. 2020;42(1):102–103. doi:10.4103/ijpsym.ijpsym_504_19