Capítulo 21 Análise robusta

21.1 Raciocínio inferencial robusto

21.1.1 O que é análise robusta?

• Análise robusta é uma abordagem estatística que busca fornecer resultados confiáveis mesmo quando as suposições clássicas dos modelos estatísticos são violadas.²³⁴

21.1.2 Por que usar análise robusta?

• Métodos clássicos como ANOVA e regressão por mínimos quadrados assumem normalidade e homocedasticidade — suposições frequentemente violadas na prática. Violações dessas suposições podem comprometer os resultados, reduzindo o poder estatístico, distorcendo os intervalos de confiança e obscurecendo as reais diferenças entre grupos.²³⁴

• Testar previamente as suposições não é suficiente: testes de homocedasticidade têm baixo poder e não garantem segurança analítica.²³⁴

• Métodos estatísticos robustos oferecem uma solução mais segura e eficaz, lidando melhor com dados não ideais.²³⁴

21.1.3 Quando usar análise robusta?

• Em alguns casos, os métodos robustos confirmam os resultados clássicos; em outros, revelam interpretações completamente diferentes. A única forma de saber o impacto real dos métodos robustos é usá-los e comparar com os métodos tradicionais.²³⁴

• Mínimos e máximos são parâmetros descritivos, mas em certas condições podem se tornar discrepantes ou influentes, distorcendo análises. Nesses casos, a análise robusta oferece alternativas mais seguras.^REF?

21.1.4 Por que métodos robustos são preferíveis?

• Métodos robustos têm a vantagem de resistir à influência de valores extremos, fornecendo medidas de posição e dispersão mais estáveis.¹⁹⁴

• Estimadores robustos oferecem maior segurança na presença de até 50% de contaminação nos dados, o que representa um ganho significativo em relação aos métodos clássicos.¹⁹⁴

21.2 Valores discrepantes

21.2.1 O que são valores discrepantes (outliers)?

• Em termos gerais, um valor discrepante — “fora da curva” ou outlier — é uma observação que possui um valor relativamente grande ou pequeno em comparação com a maioria das observações.¹⁹⁹

• Um valor discrepante é uma observação incomum que exerce influência indevida em uma análise.¹⁹⁹

• Valores discrepantes são dados com valores altos de resíduos.¹⁹²

• Nem todo valor extremo é um valor discrepante, e nem todo valor discrepante será influente.^REF?

• Alguns valores discrepantes são apenas pontos incomuns, outros de fato mudam os resultados e por isso são chamados de influentes.^REF?

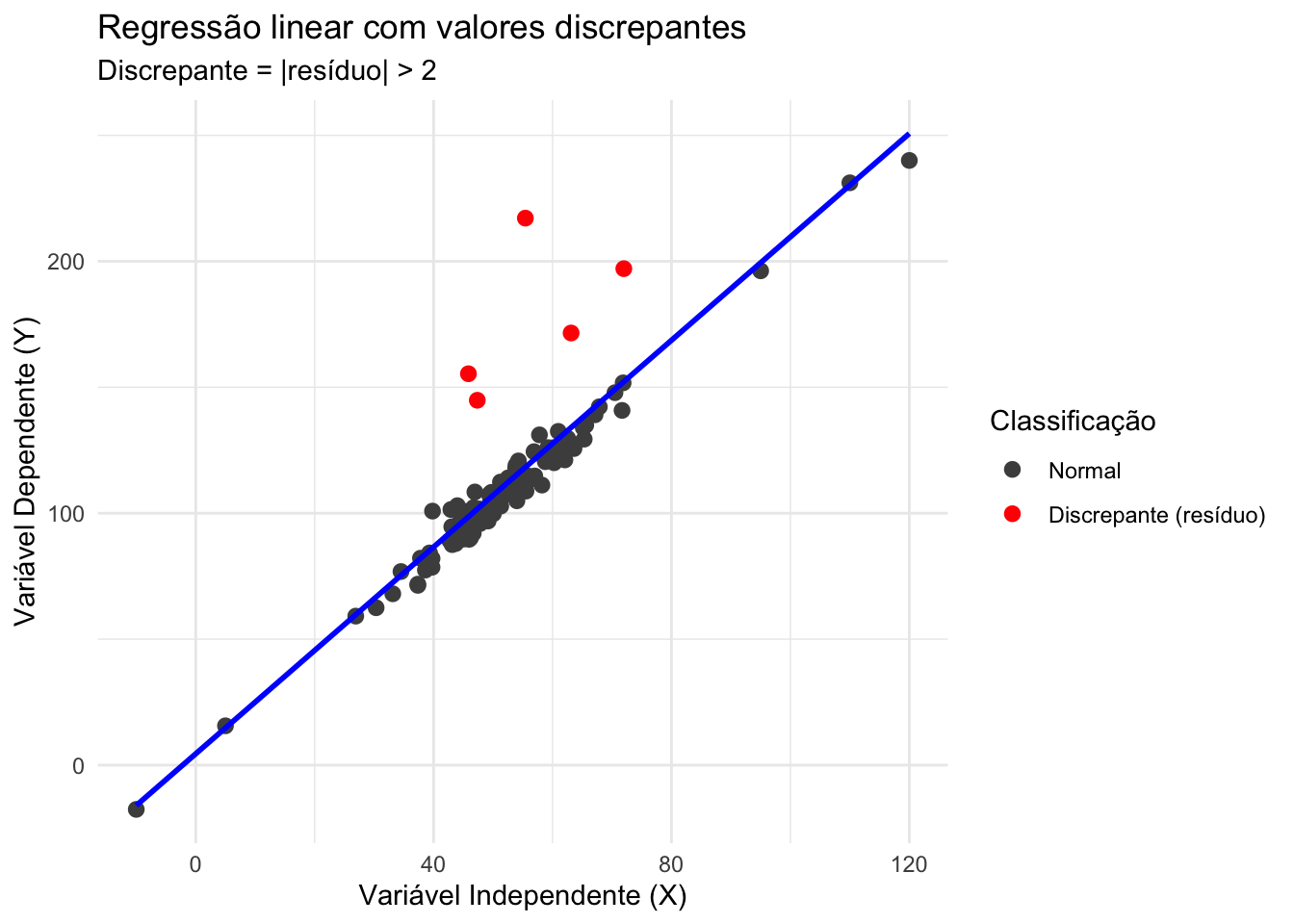
Figura 21.1: Regressão linear com valores discrepantes

21.2.2 Quais são os tipos de valores discrepantes?

• Valores discrepantes podem ser categorizados em três subtipos: outliers de erro, outliers interessantes e outliers aleatórios.¹⁹²

• Os valores discrepantes de erro são observações claramente não legítimas, distantes de outros dados devido a imprecisões por erro de mensuração e/ou codificação.¹⁹²

• Os valores discrepantes interessantes não são claramente erros, mas podem refletir um processo/mecanismo potencialmente interessante para futuras pesquisas.¹⁹²

• Os valores discrepantes aleatórios são observações que resultam por acaso, sem qualquer padrão ou tendência conhecida.¹⁹²

• Valores discrepantes podem ser univariados ou multivariados.¹⁹²

21.2.3 Por que é importante avaliar valores discrepantes?

• Excluir o valor discrepante implica em reduzir inadequadamente a variância, ao remover um valor que de fato pertence à distribuição considerada.¹⁹²

• Manter os dados inalterados (mantendo o valor discrepante) implica em aumentar inadequadamente a variância, pois a observação não pertence à distribuição que fundamenta o experimento.¹⁹²

• Em ambos os casos, uma decisão errada pode influenciar o erro do tipo I (\(\alpha\) — rejeitar uma hipótese verdadeira) ou o erro do tipo II (\(\beta\) — não rejeitar uma hipótese falsa).¹⁹²

21.2.4 Como detectar valores discrepantes?

• Na maioria das vezes, não há como saber de qual distribuição uma observação provém. Por isso, não é possível ter certeza se um valor é legítimo ou não dentro do contexto do experimento.¹⁹²

• Recomenda-se seguir um procedimento em duas etapas: detectar possíveis candidatos a outliers usando ferramentas quantitativas; e gerenciar os outliers, decidindo manter, remover ou recodificar os valores, com base em informações qualitativas.¹⁹²

• A detecção de outliers deve ser aplicada apenas uma vez no conjunto de dados; um erro comum é identificar e tratar os outliers (como remover ou recodificar) e, em seguida, reaplicar o procedimento no conjunto de dados já modificado.¹⁹²

• A detecção ou o tratamento dos outliers não deve ser realizada após a análise dos resultados, pois isso introduz viés nos resultados.¹⁹²

21.2.5 Quais são os métodos para detectar valores discrepantes?

• Valores univariados são comumente considerados outliers quando são mais extremos do que a média ± (desvio padrão × constante), podenso essa constante ser 3 (99,7% das observações estão dentro de 3 desvios-padrão da média) ou 3,29 (99,9% estão dentro de 3,29 desvios-padrão).¹⁹²

• Para detectar outliers univariados, recomenda-se o uso da Mediana da Desviação Absoluta (Median Absolute Deviation, MAD), calculado a partir de um intervalo em torno da mediana, multiplicado por uma constante (valor padrão: 1,4826).^192,235

• Para detectar outliers multivariados, comumente utiliza-se a distância de Mahalanobis, que identifica valores muito distantes do centróide formado pela maioria dos dados (por exemplo, 99%).¹⁹²

• Para detectar outliers multivariados, recomenda-se o Determinante de Mínima Covariância (Minimum Covariance Determinant, MCD), pois possui o maior ponto de quebra possível e utiliza a mediana, que é o indicador mais robusto em presença de outliers.^192,236

21.2.6 Quais testes são apropriados para detectar valores discrepantes?

• A escolha do método de detecção depende da natureza do outlier, se univariado ou multivariado.¹⁹⁴

• Para valores univariados, podem ser usados box-plots (com pontos além de 1,5 vezes o intervalo interquartílico), z-scores clássicos (\(|z| > 2.5\) ou \(|z| > 3\)) ou z-scores robustos, que substituem média por mediana e desvio-padrão por estimadores robustos.¹⁹⁴

• Para valores multivariados, recomenda-se a distância de Mahalanobis para medir o afastamento em relação ao centróide, com ajustes robustos de covariância como MCD (Minimum Covariance Determinant) ou MVE (Minimum Volume Ellipsoid).¹⁹⁴

• Técnicas baseadas em PCA robusta (ROBPCA, PP-PCA, SPCA, EPCA) também podem ser aplicadas para reduzir dimensionalidade e expor outliers mascarados.¹⁹⁴

• Métodos de trimming multivariado (MVT) podem iterativamente remover observações mais distantes, mas apresentam limitações em alta dimensionalidade.¹⁹⁴

• Estimadores com alto ponto de quebra, como o MCD, permitem detectar até 50% de outliers antes de comprometer a análise.¹⁹⁴

21.2.7 Como manejar os valores discrepantes?

• Manter outliers pode ser uma boa decisão se a maioria desses valores realmente pertence à distribuição de interesse. Manter outliers que pertencem a uma distribuição alternativa pode ser problemático, pois um teste pode se tornar significativo apenas por causa de um ou poucos outliers.¹⁹²

• Remover outliers pode ser eficaz quando eles distorcem a estimativa dos parâmetros da distribuição. Remover outliers que pertencem legitimamente à distribuição pode reduzir artificialmente a estimativa do erro.¹⁹²

• Remover outliers leva à perda de observações, especialmente em conjuntos de dados com muitas variáveis, quando outliers univariados são excluídos em cada variável.¹⁹²

• Recodificar outliers evita a perda de uma grande quantidade de dados, mas deve ser baseada em argumentos razoáveis e convincentes.¹⁹²

• Erros de observação e de medição são uma justificativa válida para descartar observações discrepantes.¹⁹⁹

21.2.8 Como conduzir análises com valores discrepantes?

• É importante reportar se existem valores discrepantes e como foram tratados.¹⁹⁹

• Valores discrepantes na variável de desfecho podem exigir uma abordagem mais refinada, especialmente quando representam uma variação real na variável que está sendo medida.¹⁹⁹

• Valores discrepantes em uma (co)variável podem surgir devido a um projeto experimental inadequado; nesse caso, abandonar a observação ou transformar a covariável são opções adequadas.¹⁹⁹

• Valores discrepantes podem ser recodificados usando a Winsorização,²³⁷ que transforma os outliers em valores de percentis específicos (como o 5º e o 95º).¹⁹²

O pacote outliers²³⁸ fornece a função outlier para identificar os valores mais distantes da média.

O pacote outliers²³⁸ fornece a função rm.outlier para remover os valores mais distantes da média detectados por testes de hipótese e/ou substitui-los pela média ou mediana.

21.2.9 Como lidar com outliers na análise exploratória de dados?

• Após a detecção, três estratégias principais podem ser adotadas: (1) manter os outliers, (2) removê-los ou (3) recodificá-los (por exemplo, com Winsorização). A escolha deve ser justificada com base no contexto teórico e nas características do banco de dados. Idealmente, erros devem ser corrigidos ou removidos, enquanto outliers interessantes podem gerar novas hipóteses de pesquisa.¹⁹²

• A decisão sobre como lidar com outliers deve ser definida a priori e preferencialmente registrada em plataformas de pré-registro. Essa prática aumenta a transparência, reduz a flexibilidade analítica e evita inflar taxas de erro tipo I.¹⁹²

21.3 Valores influentes

21.3.1 O que são valores influentes?

• Valores influentes são observações que, se removidas, causariam uma mudança significativa nos resultados da análise estatística.^REF?

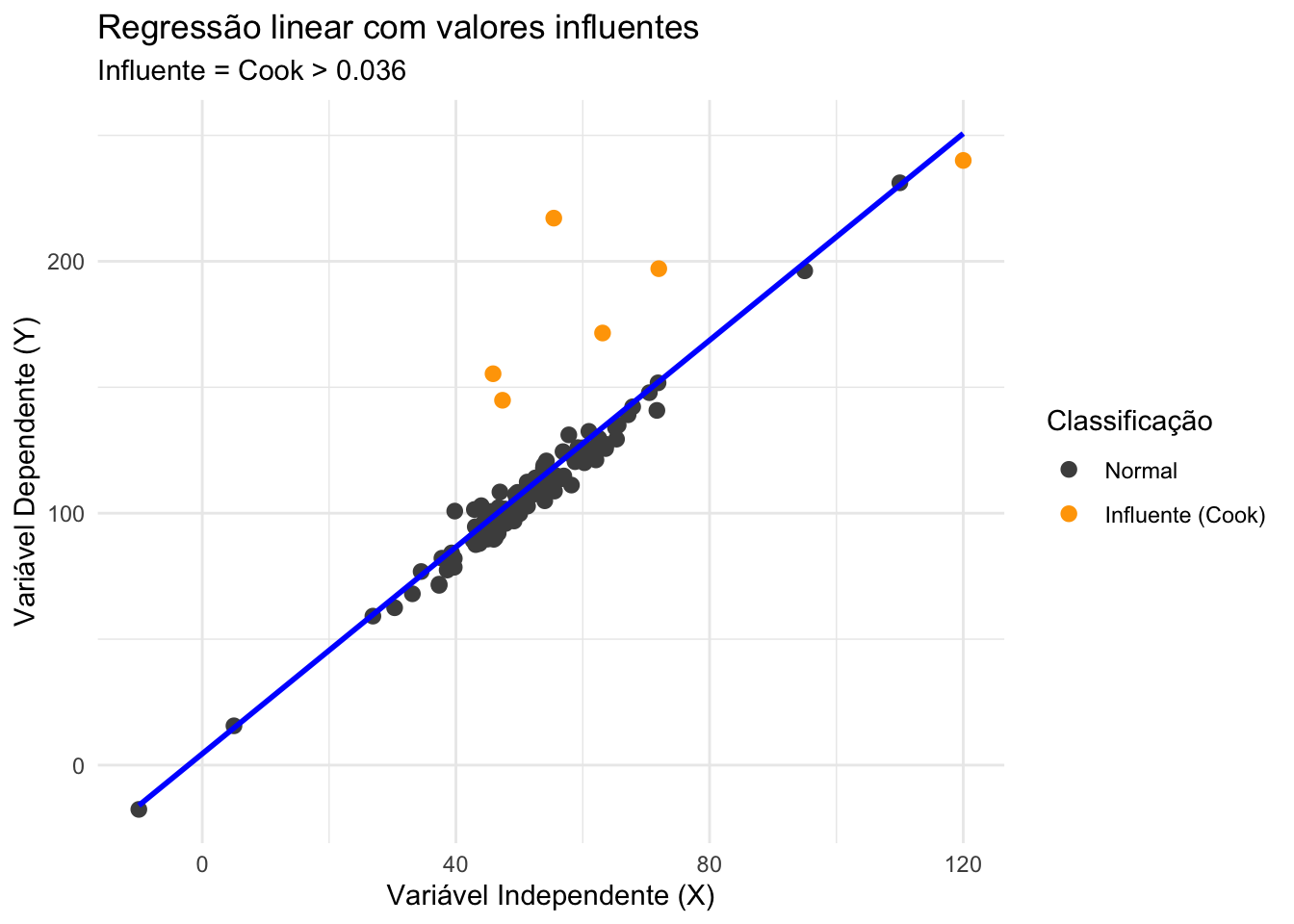
Figura 21.2: Regressão linear com valores influentes.

21.3.2 O que é função de influência?

• A função de influência mede a sensibilidade de um estimador a pequenas contaminações nos dados. Um estimador é considerado robusto se sua função de influência for limitada, indicando que valores extremos não exercem impacto desproporcional.²³⁹

21.3.3 O que é ponto de quebra?

• O ponto de quebra representa a fração mínima de observações contaminadas necessária para distorcer um estimador até o infinito. Por exemplo, a média tem ponto de quebra 0, enquanto a mediana atinge o ponto de quebra máximo (50%).²³⁹

21.3.4 Como detectar valores influentes?

• A alavancagem (leverage) mede o quão distante uma observação está dos valores médios das variáveis independentes. Observações com alta alavancagem têm o potencial de influenciar significativamente a linha de regressão.^REF?

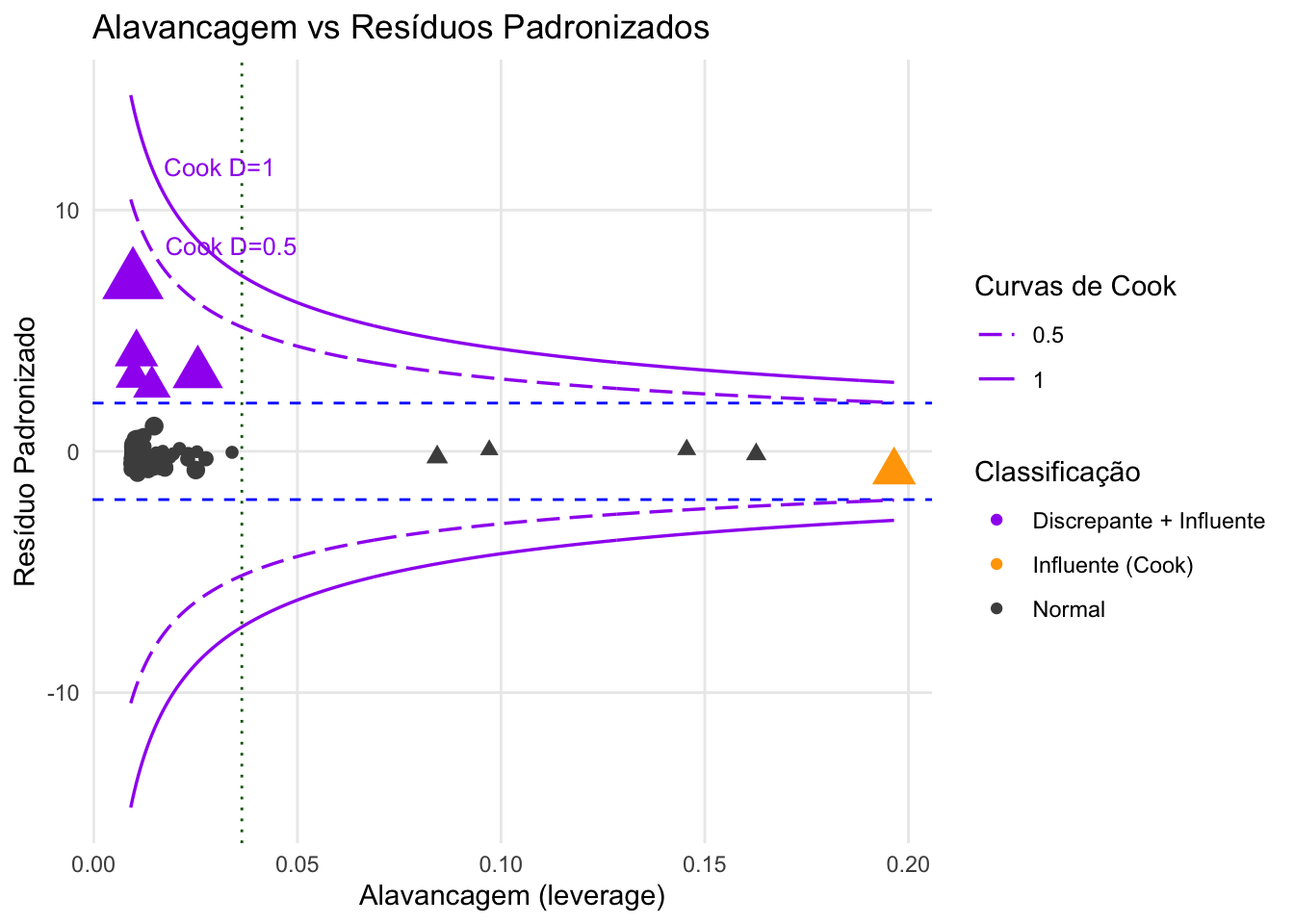
Figura 21.3: Alavancagem vs Resíduos Padronizados com distância de Cook para análise da influência de pontos.

21.4 Métodos robustos de tratamento de outliers

21.4.1 O que é Winsorização?

• Winsorização é uma técnica que substitui os valores extremos (outliers) por valores menos extremos, preservando a estrutura dos dados. Isso é feito definindo limites superior e inferior e substituindo os valores que ultrapassam esses limites pelos próprios limites.²³⁴

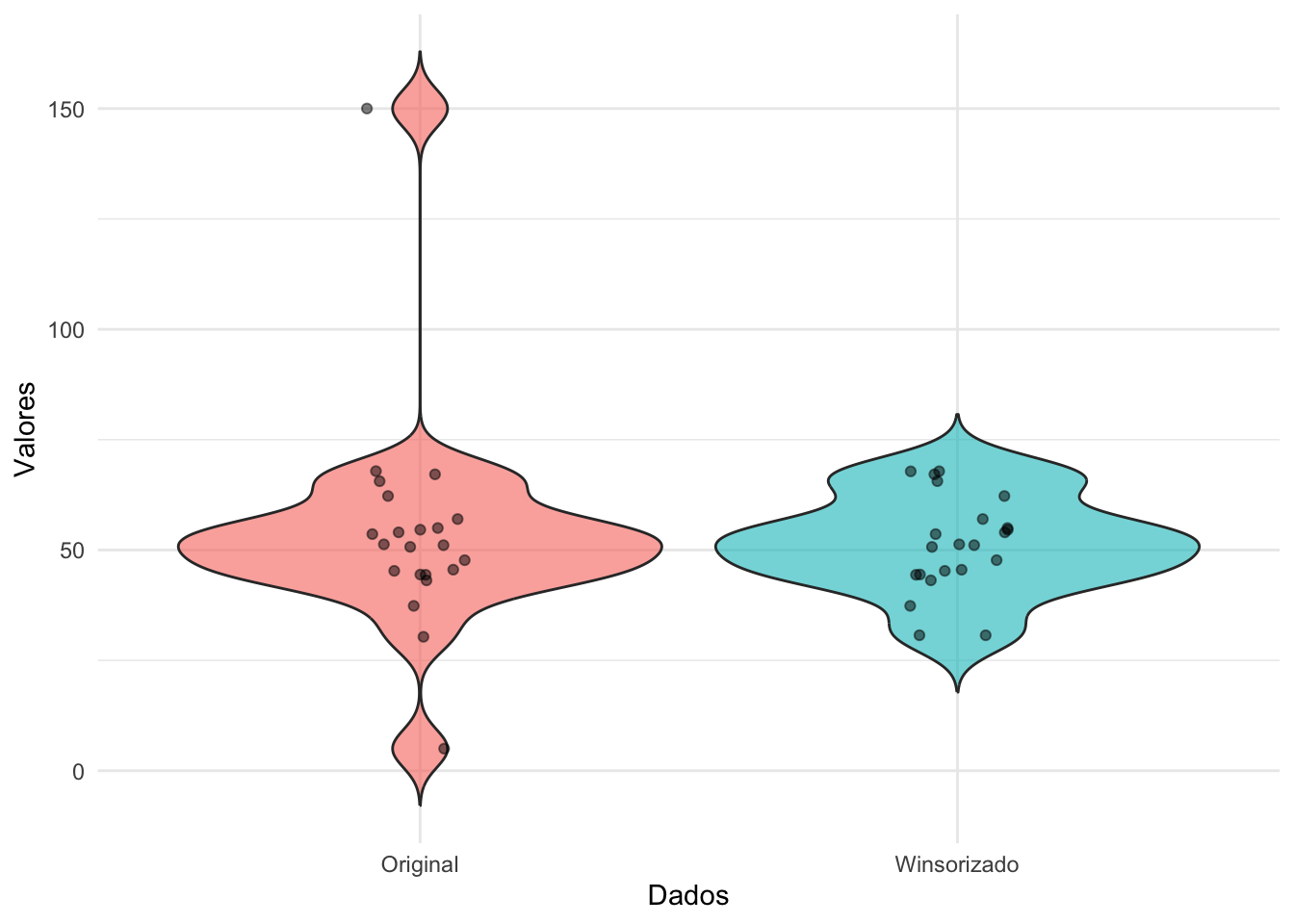
Figura 21.4: Boxplots comparando dados originais e dados Winsorizados.

21.4.2 Quais são as alternativas à Winsorização?

• Podar (trimming): remove diretamente uma fração fixa das observações mais extremas.^REF?

• Estimadores robustos: resistem à influência de outliers sem transformar os dados.^REF?

• Transformações de variáveis: reduzem a assimetria e impacto de valores extremos, mas mudam a escala interpretativa.^REF?

O pacote WRS2²⁴⁰ fornece as funções winmean e winvar para calcular a média e variância Winsorizadas.

O pacote WRS2²⁴⁰ fornece a função yuen para realizar o teste de comparação de Yuen de médias Winsorizadas para amostras independentes ou dependentes.

O pacote WRS2²⁴⁰ fornece a função wincor para calcular a correlação Winsorizada.

O pacote WRS2²⁴⁰ fornece as funções t1way, t2way e t3way para realizar testes de comparação de médias Winsorizadas para análise de variância para 1, 2 ou 3 fatores, respectivamente.

Citar como:
Ferreira, Arthur de Sá. Ciência com R: Perguntas e respostas para pesquisadores e analistas de dados. Rio de Janeiro: 1a edição,

Referências

192.

Leys C, Delacre M, Mora YL, Lakens D, Ley C. How to Classify, Detect, and Manage Univariate and Multivariate Outliers, With Emphasis on Pre-Registration. International Review of Social Psychology. 2019;32(1). doi:10.5334/irsp.289

194.

Daszykowski M, Kaczmarek K, Vander Heyden Y, Walczak B. Robust statistics in data analysis A review. Chemometrics and Intelligent Laboratory Systems. 2007;85(2):203–219. doi:10.1016/j.chemolab.2006.06.016

199.

Zuur AF, Ieno EN, Elphick CS. A protocol for data exploration to avoid common statistical problems. Methods in Ecology and Evolution. 2009;1(1):3–14. doi:10.1111/j.2041-210x.2009.00001.x

234.

Mair P, Wilcox R. Robust Statistical Methods in R Using the WRS2 Package. Behavior Research Methods. 2020;52:464–488. doi:10.3758/s13428-019-01246-w

235.

Leys C, Ley C, Klein O, Bernard P, Licata L. Detecting outliers: Do not use standard deviation around the mean, use absolute deviation around the median. Journal of Experimental Social Psychology. 2013;49(4):764–766. doi:10.1016/j.jesp.2013.03.013

236.

Leys C, Klein O, Dominicy Y, Ley C. Detecting multivariate outliers: Use a robust variant of the Mahalanobis distance. Journal of Experimental Social Psychology. 2018;74:150–156. doi:10.1016/j.jesp.2017.09.011

237.

Tukey JW, McLaughlin DH. Less Vulnerable Confidence and Significance Procedures for Location Based on a Single Sample: Trimming/Winsorization 1. Sankhyā: The Indian Journal of Statistics, Series A (1961-2002). 1963;25(3):331–352. http://www.jstor.org/stable/25049278. Acessado abril 11, 2025.

238.

Komsta L. outliers: Tests for Outliers.; 2022. https://CRAN.R-project.org/package=outliers.

239.

Loh PL. A Theoretical Review of Modern Robust Statistics. Annual Review of Statistics and Its Application. 2025;12(1):477–496. doi:10.1146/annurev-statistics-112723-034446

240.

Mair P, Wilcox R, Indrajeet P. A Collection of Robust Statistical Methods.; 2025. https://CRAN.R-project.org/package=WRS2.