Capítulo 33 Correlação

33.1 Análise inferencial de correlação

33.1.1 O que é covariância?

.^REF?

33.1.2 O que é correlação?

.^REF?

33.1.3 Qual é a interpretação das medidas de correlação?

Os valores de correlação estão no intervalo \([-1; 1]\).^115,299,300
Valores de correlação positivos representam uma relação direta entre as variáveis, tal que valores maiores de uma variável estão associados a valores maiores de outra variável.^299,300
Valores de correlação negativos representam uma relação indireta (ou inversa) entre as variáveis, tal que valores maiores (menores) de uma variável estão associados a valores maiores (menores) de outra variável.^299,300
Valores de correlação próximos de \(0\) representam a inexistência de relação entre as variáveis.^299,300

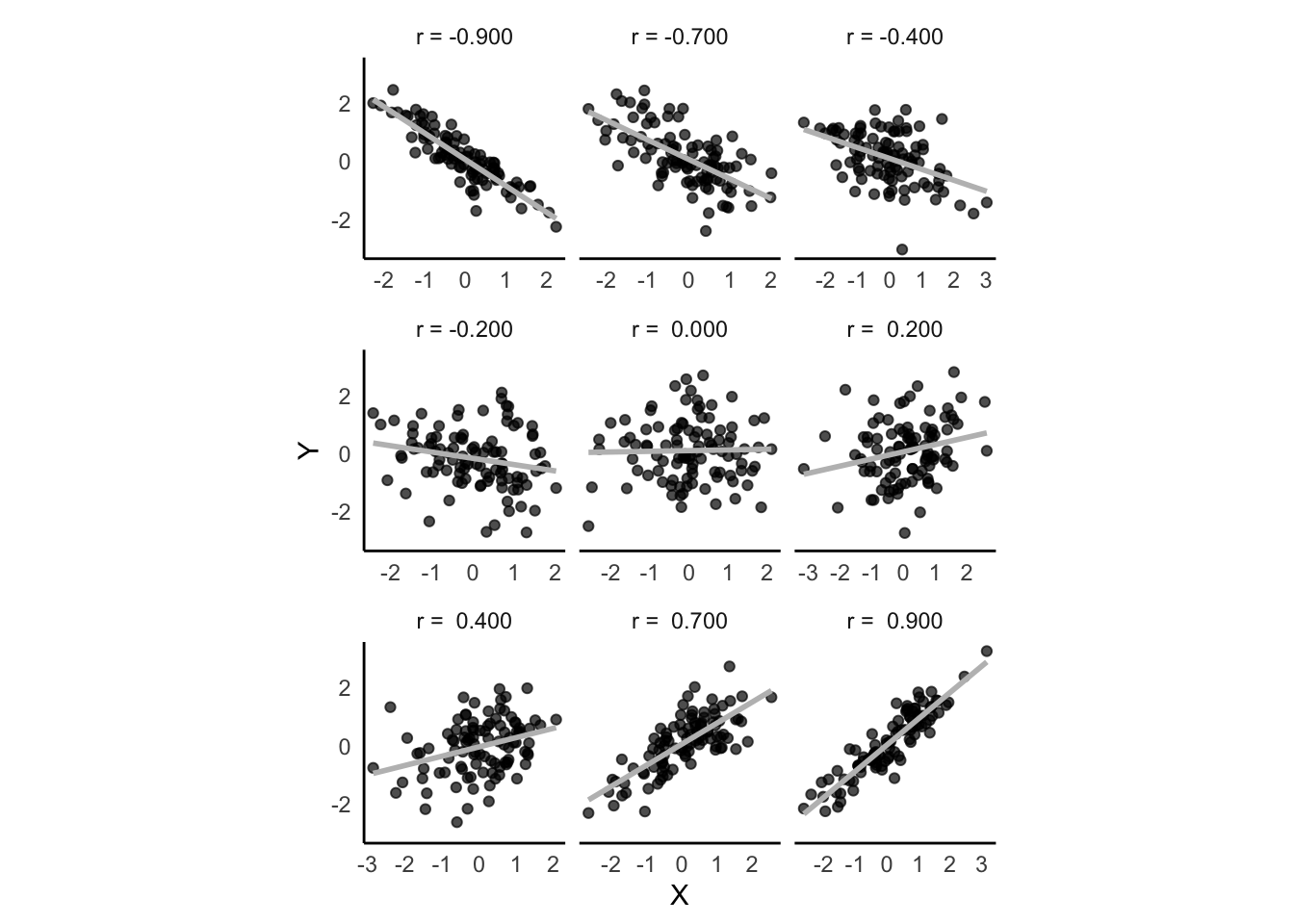
Figura 33.1: Exemplo de diferentes forças e direção de correlação entre duas variáveis X e Y.

33.1.4 Quais precauções devem ser tomadas na interpretação de medidas de correlação?

Tamanhos de efeito grande (ou qualquer outro) não representam necessariamente uma relação causa-efeito entre as variáveis.²⁹⁹
Tamanhos de efeito grande (ou qualquer outro) não representam necessariamente uma relação de concordância ou confiabilidade entre as variáveis.²⁹⁹
Uma escala de medição com representação agregada do constructo na coleta de dados pode subestimar o tamanho do efeito da correlação \(r\) em de cerca de 13% e do coeficiente de determinação \(R^2\) de cerca de 30%.¹²⁸ Neste caso, a correlação desatenuada \(r_{x'y'}\) pode ser calculada por (33.1), utilizando a correlação observada \(r_{xy}\) e os fatores de correção \(r_{xx'}\) e \(r_{yy'}\) para o número de intervalos nas variáveis X e Y, respectivamennte:¹²⁸

\[\begin{equation} \tag{33.1} r_{x'y'} = \dfrac{r_{xy}}{r_{xx'}r_{yy'}} \end{equation}\]

O pacote psychmeta³⁰¹ fornece a função correct_r_coarseness para calcular o coeficiente de correlação desatenuado (\(r_{x'y'}\)).

O pacote psychmeta³⁰¹ fornece a função correct_r para calcular o coeficiente de correlação em escala restrita e/ou com erro de mensuração (\(r_{x'y'}\)).

Os coeficientes de correlação possuem suposições que, se violadas, podem levar a interpretações equivocadas. Nestes cenários, visualizar os dados e as relações entre as variáveis pode contribuir com a interpretação e utilidade dos coeficientes de correlação.³⁰²
O quarteto de Anscombe é um conjunto de quatro bancos de dados bivariados que possuem a mesma média, variância, correlação e regressão linear (até a 2a casa decimal), mas que são visualmente diferentes e, assim, demonstram a importância da análise gráfica da correlação.³⁰²

Tabela 33.1: Quarteto de Anscombe.
ID	x1	x2	x3	x4	y1	y2	y3	y4
1	10	10	10	8	8.04	9.14	7.46	6.58
2	8	8	8	8	6.95	8.14	6.77	5.76
3	13	13	13	8	7.58	8.74	12.74	7.71
4	9	9	9	8	8.81	8.77	7.11	8.84
5	11	11	11	8	8.33	9.26	7.81	8.47
6	14	14	14	8	9.96	8.10	8.84	7.04
7	6	6	6	8	7.24	6.13	6.08	5.25
8	4	4	4	19	4.26	3.10	5.39	12.50
9	12	12	12	8	10.84	9.13	8.15	5.56
10	7	7	7	8	4.82	7.26	6.42	7.91
11	5	5	5	8	5.68	4.74	5.73	6.89

Tabela 33.2: Análise descritiva do Quarteto de Anscombe demostrando os conjuntos de dados bivariados com parâmetros quase idênticos.
	X1Y1	X2Y2	X3Y3	X4Y4
Observações	11.00	11.00	11.00	11.00
Média x	9.00	9.00	9.00	9.00
Média y	7.50	7.50	7.50	7.50
Variância x	11.00	11.00	11.00	11.00
Variância y	4.13	4.13	4.12	4.12
Correlação	0.82	0.82	0.82	0.82
Coeficiente angular	0.50	0.50	0.50	0.50
Coeficiente linear	3.00	3.00	3.00	3.00
Coeficiente de determinação	0.67	0.67	0.67	0.67

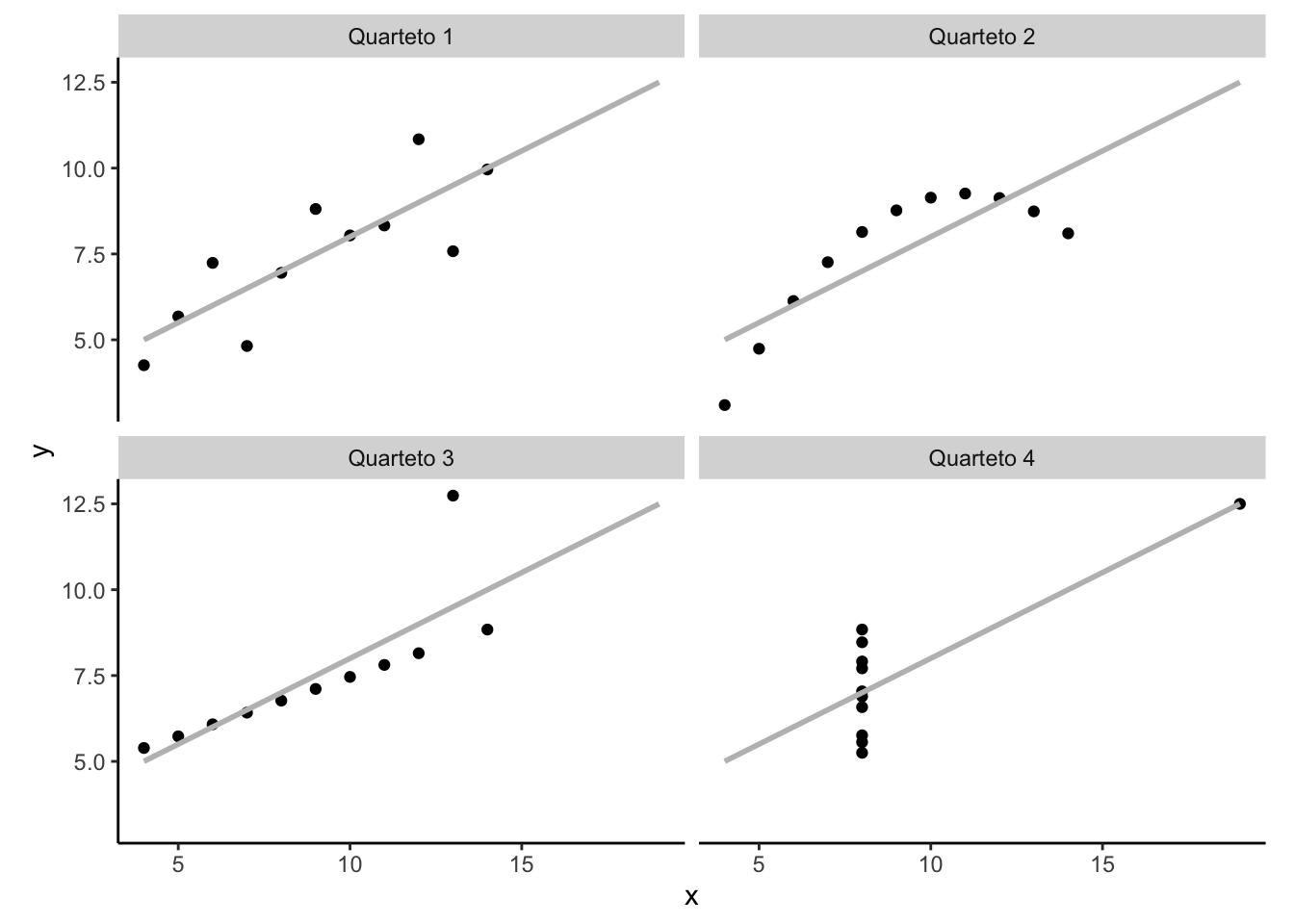
Gráfico de dispersão do Quarteto de Anscombe para representação gráfica de conjuntos de dados bivariados com parâmetros quase idênticos e relações muito distintas.

Figura 33.2: Gráfico de dispersão do Quarteto de Anscombe para representação gráfica de conjuntos de dados bivariados com parâmetros quase idênticos e relações muito distintas.

O pacote anscombiser³⁰³ fornece a função anscombise para gerar bancos de dados que compartilham os mesmos valores de parâmetros do Quarteto de Anscombe.

33.2 Coeficientes de correlação

33.2.1 Quais coeficientes podem ser usados em análises de correlação?

Coeficiente de correlação de Pearson (\(r\)) (33.2).^299,300

\[\begin{equation} \tag{33.2} r = \dfrac{n \sum{x_i y_i} - \sum{x_i} \sum{y_i}}{\sqrt{\left[n \sum{x_i^2} - (\sum{x_i})^2\right]\left[n \sum{y_i^2} - (\sum{y_i})^2\right]}} \end{equation}\]

O coeficiente de correlação de Pearson (\(r\)) avalia a força e direção da relação linear entre duas variáveis quantitativas.^299,300
Tipo: paramétrico.^299,300
Hipóteses:³⁰⁰
Nula (\(H_{0}\)): \(r=0\)
Alternativa (\(H_{1}\)): \(r≠0\)
Tamanho do efeito:^299,300
Coeficiente de correlação de Pearson (\(r\))

O pacote stats¹³⁴ fornece a função cor.test para calcular o coeficiente de correlação de Pearson (\(r\)).

O pacote correlation³⁰⁴ do projeto easystats³⁰⁵ fornece a função correlation para calcular o coeficiente de correlação de Pearson (\(r\)).

Coeficiente de correlação ponto-bisserial (\(r_{s}\)) (33.3).²⁹⁹

\[\begin{equation} \tag{33.3} r_{s} = \dfrac{M_{1} - M_{0}}{s_{y}} \sqrt{\dfrac{n_{1}n_{0}}{n^2}} \end{equation}\]

O coeficiente de correlação ponto-bisserial (\(r_{s}\)) avalia a força e direção da relação linear entre uma variável quantitativa e outra dicotômica.²⁹⁹
Tipo: paramétrico.²⁹⁹
Hipóteses:²⁹⁹
Nula (\(H_{0}\)): \(r_{s}=0\)
Alternativa (\(H_{1}\)): \(r_{s}≠0\)
Tamanho do efeito:²⁹⁹
Coeficiente de correlação ponto-bisserial (\(r_{s}\))

O pacote stats¹³⁴ fornece a função cor.test para calcular o coeficiente de correlação ponto-bisserial (\(r_{s}\)).

O pacote correlation³⁰⁴ do projeto easystats³⁰⁵ fornece a função correlation para calcular o coeficiente de correlação ponto-bisserial (\(r_{s}\)).

Coeficiente de correlação de Spearman (\(\rho\)) (33.4).^299,300

\[\begin{equation} \tag{33.4} \rho = 1 - \dfrac{6 \Sigma d_{i}^2}{n(n^2 - 1)} \end{equation}\]

O coeficiente de correlação de Spearman (\(\rho\)) avalia a força e direção da relação monotônica entre duas variáveis quantitativas.^299,300
O coeficiente de correlação de Spearman (\(\rho\)) pode ser também definida como a correlação de Pearson (\(r\)) entre as classificações (ranks) das duas variáveis quantitativas.^299,300
Tipo: não-paramétrico.^299,300
Hipóteses:^299,300
Nula (\(H_{0}\)): \(\rho=0\)
Alternativa (\(H_{1}\)): \(\rho≠0\)
Tamanho do efeito:^299,300
Coeficiente de correlação de Spearman (\(\rho\))

O pacote stats¹³⁴ fornece a função cor.test para calcular o coeficiente de correlação de Spearman (\(\rho\)).

O pacote correlation³⁰⁴ do projeto easystats³⁰⁵ fornece a função correlation para calcular o coeficiente de correlação de Spearman (\(\rho\)).

Coeficiente de Kendall (\(\tau\)) (33.5).^299,300

\[\begin{equation} \tag{33.5} \tau = \dfrac{(n_{c} - n_{d})}{\dfrac{1}{2}n(n-1)} \end{equation}\]

O coeficiente Kendall \(\tau\) avalia a força e direção da relação monotônica entre duas variáveis quantitativas ou qualitativas.^299,300
O coeficiente Kendall \(\tau\) é definido como a proporção de todos os pares concordantes menos a proporção de todos os pares discordantes.^299,300
Tipo: não-paramétrico.^299,300
Hipóteses:^299,300
Nula (\(H_{0}\)): \(\tau=0\)
Alternativa (\(H_{1}\)): \(\tau≠0\)
Tamanho do efeito:^299,300
Kendall \(\tau\)

O pacote stats¹³⁴ fornece a função cor.test para calcular o coeficiente Kendall \(\tau\).

O pacote correlation³⁰⁴ do projeto easystats³⁰⁵ fornece a função correlation para calcular o coeficiente coeficiente Kendall \(\tau\).

Coeficiente de Cramér (\(V\)) (33.6).^REF?

\[\begin{equation} \tag{33.6} V = \sqrt{\dfrac{\chi^2/n}{\min(k-1, r-1)}} \end{equation}\]

O coeficiente Cramér (\(V\)) avalia a força e direção da relação entre duas variáveis qualitativas.^REF?
Tipo: não-paramétrico.^REF?
Hipóteses:^REF?
Nula (\(H_{0}\)): \(V=0\)
Alternativa (\(H_{1}\)): \(V≠0\)
Tamanho do efeito:^REF?
Coeficiente Cramer (\(V\))

Coeficiente de Sheperd (\(\phi\)) (33.7).^REF?

\[\begin{equation} \tag{33.7} \phi = \sqrt{\dfrac{\chi^2}{n}} \end{equation}\]

O coeficiente Phi (\(\phi\)) avalia a força e direção da relação entre duas variáveis dicotômicas.^REF?
Tipo: não-paramétrico.^REF?
Hipóteses:^REF?
Nula (\(H_{0}\)): \(\phi=0\)
Alternativa (\(H_{1}\)): \(\phi≠0\)
Tamanho do efeito:^REF?
Coeficiente Phi (\(\phi\))

O pacote correlation³⁰⁴ do projeto easystats³⁰⁵ fornece a função correlation para calcular o coeficiente coeficiente Sheperd \(\phi\).

O pacote corrplot²²⁹ fornece a função cor.mtest para calcular os P-valores e intervalos de confiança da matriz de correlação.

O pacote corrplot²²⁹ fornece a função corrplot para visualização da matriz de correlação.

33.3 Colinearidade

33.3.1 O que é colinearidade?

Colinearidade representa a correlação entre duas variáveis.³⁰⁶
Colinearidade exata indica uma relação linear perfeita entre duas variáveis.³⁰⁶

33.3.2 Como identificar colinearidade na matriz de correlação?

A colinearidade pode ser identificada na matriz de correlação por meio da análise dos coeficientes de correlação entre as variáveis.³⁰⁶
Valores de correlação próximos de \(1\) ou \(-1\) indicam colinearidade entre as variáveis.³⁰⁶

O pacote GGally³⁰⁷ fornece a função ggally_cor para estimar a correlação bivariada e exibir o coeficiente de correlação e o P-valor na matriz de correlação.³⁰⁷

33.4 Correlação entre conjuntos de variáveis

33.4.1 O que é correlação entre conjuntos de variáveis?

A Correlação Canônica (CCA) analisa a relação entre dois conjuntos de variáveis simultaneamente.^REF?
Busca combinações lineares que maximizam a correlação entre os dois blocos.^REF?

33.4.2 Quando usar CCA?

Quando existem dois blocos distintos de variáveis.^REF?
Quando a correlação bivariada é insuficiente para captar padrões multivariados.^REF?

33.4.3 Quais são os principais resultados?

Correlação canônica (\(\rho_1\), \(\rho_2\), \(...\)): força da associação entre os escores dos blocos.^REF?
Escores canônicos (\(U\) e \(V\)): novas variáveis representando os blocos.^REF?
Loadings e cross-loadings: indicam quais variáveis mais contribuem para cada eixo.^REF?

33.4.4 Como interpretar a CCA?

\(\rho_1\) indica a força do primeiro eixo canônico (\(U_1 \leftrightarrow V_1\)).^REF?
Gráficos de \(U_1\) vs \(V_1\) podem revelar padrões por grupo ou gradiente.^REF?
Loadings/cross-loadings mostram quais variáveis explicam a correlação.^REF?

33.4.5 Quais suposições e cuidados?

As variáveis devem estar padronizadas (escalas comparáveis).^REF?
Preferível \(n>\) número de variáveis em cada bloco.^REF?
Atenção a multicolinearidade alta (pode exigir CCA regularizada).^REF?

33.4.6 O que reportar nos resultados?

Valores de \(\rho_1\), \(\rho_2\), \(...\) comteste de Wilks e p-valores.^REF?
Figura \(U_1\) vs. \(V_1\) com interpretação.^REF?
Tabela de loadings ou cross-loadings destacando contribuições relevantes.^REF?
Uma interpretação substantiva da relação entre os blocos.^REF?

Code

# Reproducibilidade
set.seed(123)

# Suponha X: variáveis ambientais; Y: traços de plantas
n  <- 120
X  <- scale(cbind(pH = rnorm(n, 6.5, .4),
temp = rnorm(n, 20, 3),
rain = rnorm(n, 1000, 120)))
Y  <- scale(cbind(height = 0.4*X[, "temp"] - 0.3*X[, "pH"] + rnorm(n,0,.6),
leaf   = 0.3*X[, "rain"] + 0.25*X[, "temp"] + rnorm(n,0,.6),
chl    = -0.35*X[, "pH"] + 0.3*X[, "rain"] + rnorm(n,0,.6)))

# (Opcional) fator de cor para o scatter
classe <- factor(sample(c("Forest","Herb","Planted","Shrub"), n, TRUE))

# ---- CCA (base R) ----
fit <- cancor(X, Y)   # stats::cancor
rho <- fit$cor        # correlações canônicas

# Escores canônicos (U e V)

U <- scale(X) %*% fit$xcoef
V <- scale(Y) %*% fit$ycoef
U1 <- U[,1]; V1 <- V[,1]

# ---- Teste sequencial (Wilks) ----

# wilks <- CCP::p.asym(rho, N=n, p=ncol(X), q=ncol(Y), tstat="Wilks")
# wilks_tab <- transform(wilks, rho=round(rho,3),
# p.value=signif(p.value,3))

# ---- Loadings e cross-loadings (correlações com escores) ----

# Loadings: var-X com U1.., var-Y com V1..

loadX <- cor(X, U[,1:min(ncol(X), ncol(Y))])
loadY <- cor(Y, V[,1:min(ncol(X), ncol(Y))])

# Cross-loadings: var-X com V1.., var-Y com U1..

crossX <- cor(X, V[,1:min(ncol(X), ncol(Y))])
crossY <- cor(Y, U[,1:min(ncol(X), ncol(Y))])

# common limits for U1 and V1
lims <- range(c(U1, V1), na.rm = TRUE)

p1_equal <- ggplot2::ggplot(
  data.frame(U1 = U1, V1 = V1, classe = classe),
  ggplot2::aes(U1, V1, shape = classe)
) +
  ggplot2::geom_point(alpha = .75) +
  ggplot2::geom_smooth(method = "lm", se = FALSE) +
  ggplot2::scale_x_continuous(limits = lims) +
  ggplot2::scale_y_continuous(limits = lims) +
  ggplot2::coord_fixed() +
  ggplot2::labs(
    x = "U1 (X → a1)",
    y = "V1 (Y → b1)",
    subtitle = paste0("ρ1 = ", round(rho[1], 3))
  ) +
  ggplot2::theme_minimal()

print(p1_equal)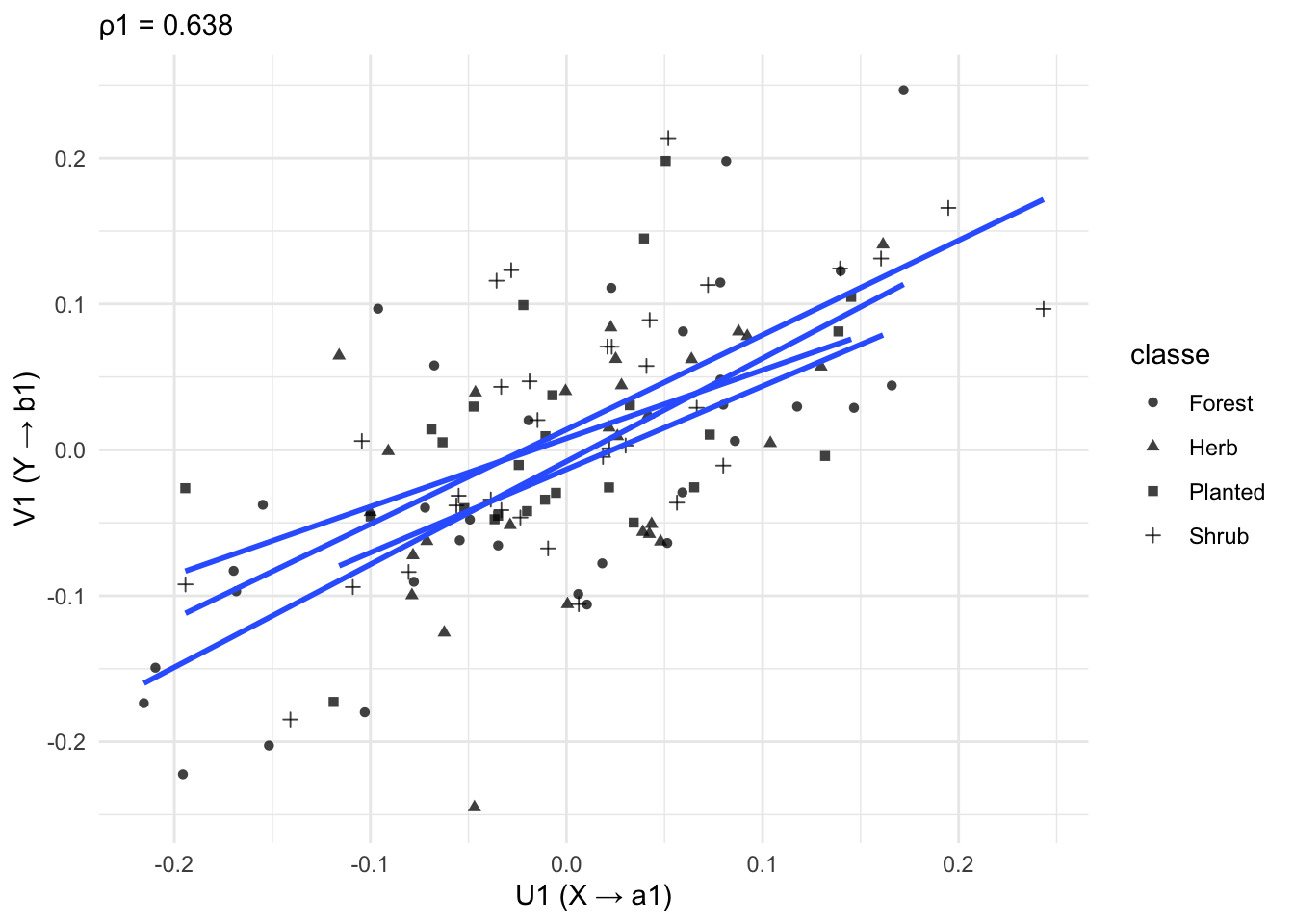

Figura 33.3: Exemplo de análise de correlação canônica (CCA) entre dois conjuntos de variáveis.

Citar como:
Ferreira, Arthur de Sá. Ciência com R: Perguntas e respostas para pesquisadores e analistas de dados. Rio de Janeiro: 1a edição,

Referências

115.

Barkan H. Statistics in clinical research: Important considerations. Annals of Cardiac Anaesthesia. 2015;18(1):74. doi:10.4103/0971-9784.148325

128.

Aguinis H, Pierce CA, Culpepper SA. Scale Coarseness as a Methodological Artifact. Organizational Research Methods. 2008;12(4):623–652. doi:10.1177/1094428108318065

134.

R Core Team. R: A Language and Environment for Statistical Computing.; 2025. https://www.R-project.org/.

229.

Wei T, Simko V. R package corrplot: Visualization of a Correlation Matrix.; 2024. https://github.com/taiyun/corrplot.

299.

Khamis H. Measures of Association: How to Choose? Journal of Diagnostic Medical Sonography. 2008;24(3):155–162. doi:10.1177/8756479308317006

300.

Allison JS, Santana L, (Jaco) Visagie IJH. A primer on simple measures of association taught at undergraduate level. Teaching Statistics. 2022;44(3):96–103. doi:10.1111/test.12307

301.

Dahlke JA, Wiernik BM. psychmeta: An R Package for Psychometric Meta-Analysis. Applied Psychological Measurement. 2018;43(3):415–416. doi:10.1177/0146621618795933

302.

Anscombe FJ. Graphs in Statistical Analysis. The American Statistician. 1973;27(1):17–21. doi:10.1080/00031305.1973.10478966

303.

Northrop PJ. anscombiser: Create Datasets with Identical Summary Statistics.; 2022. https://CRAN.R-project.org/package=anscombiser.

304.

Makowski D, Wiernik BM, Patil I, Lüdecke D, Ben-Shachar MS. correlation: Methods for Correlation Analysis.; 2022. https://CRAN.R-project.org/package=correlation.

305.

Lüdecke D, Ben-Shachar MS, Patil I, et al. easystats: Framework for Easy Statistical Modeling, Visualization, and Reporting.; 2022. https://easystats.github.io/easystats/.

306.

Kim JH. Multicollinearity and misleading statistical results. Korean Journal of Anesthesiology. 2019;72(6):558–569. doi:10.4097/kja.19087

307.

Schloerke B, Cook D, Larmarange J, et al. GGally: Extension to ggplot2.; 2024. doi:10.32614/CRAN.package.GGally