Capítulo 10 Variáveis e fatores

10.1 Variáveis

10.1.1 O que são variáveis?

• Variáveis são informações que podem variar entre medidas em diferentes indivíduos e/ou repetições.¹¹⁰

• Variáveis definem características de uma amostra extraída da população, tipicamente observados por aplicação de métodos de amostragem (isto é, seleção) da população de interesse.¹¹¹

10.1.2 Como são classificadas as variáveis?

• Quanto à informação:^111–114

  • Quantitativa

  • Qualitativa

• Quanto ao conteúdo:^111–115

  • Contínua: representam ordem e magnitude entre valores.

    • Discreta (valores inteiros ou contáveis) vs. Contínua (valores em escala contínua).

    • Intervalo (valor ‘0’ é arbitrário) vs. Razão (valor ‘0’ verdadeiro).

  • Categórica ordinal (numérica ou nominal): representam ordem, mas não magnitude entre valores.

  • Categórica nominal (multinominal ou dicotômica): não representam ordem ou magnitude, apenas categorias.

• Quanto à interpretação:^111–114

  • Dependente (desfecho)

  • Independente (preditora, covariável, confundidora, controle)

  • Mediadora

  • Moderadora

  • Modificadora

  • Auxiliar

  • Indicadora

O pacote base⁵⁷ fornece a função class para identificar qual é o tipo do objeto.

O pacote base⁵⁷ fornece as funções as.numeric e as.character para criar objetos numéricos e categóricos, respectivamente.

O pacote base⁵⁷ fornece as funções as.Date e as.logical para criar objetos em formato de data e lógicos (VERDADEIRO, FALSO), respectivamente.

10.2 Transformação de variáveis

10.2.1 Por que é importante classificar as variáveis?

• Identificar corretamente os tipos de variáveis da pesquisa é uma das etapas da escolha dos métodos estatísticos adequados para as análises e representações no texto, tabelas e gráficos.¹¹³

10.2.2 O que é transformação de variáveis?

• Transformação significa aplicar uma função matemática à variável medida em sua unidade original.¹¹⁶

• A transformação visa atender aos pressupostos dos modelos estatísticos quanto à distribuição da variável, em geral a distribuição gaussiana.^111,116

• A dicotomização pode ser interpretada como um caso particular de agrupamento.¹¹⁷

10.2.3 Por que transformar variáveis?

• Muitos procedimentos estatísticos supõem que as variáveis — ou seus termos de erro, mais especificamente — são normalmente distribuídas. A violação dessa suposição pode aumentar suas chances de cometer um erro do tipo I ou II.¹¹⁸

• Mesmo quando se está usando análises consideradas robustas para violações dessas suposições ou testes não paramétricos (que não assumem explicitamente termos de erro normalmente distribuídos), atender a essas questões pode melhorar os resultados das análises (por exemplo, Zimmerman, 1995).¹¹⁸

10.2.4 Quais transformações de variáveis podem ser aplicadas?

• Distribuições com assimetria à direita: raiz quadrada, logaritmo natural, logaritmo base 10, transformação inversa.¹¹⁸

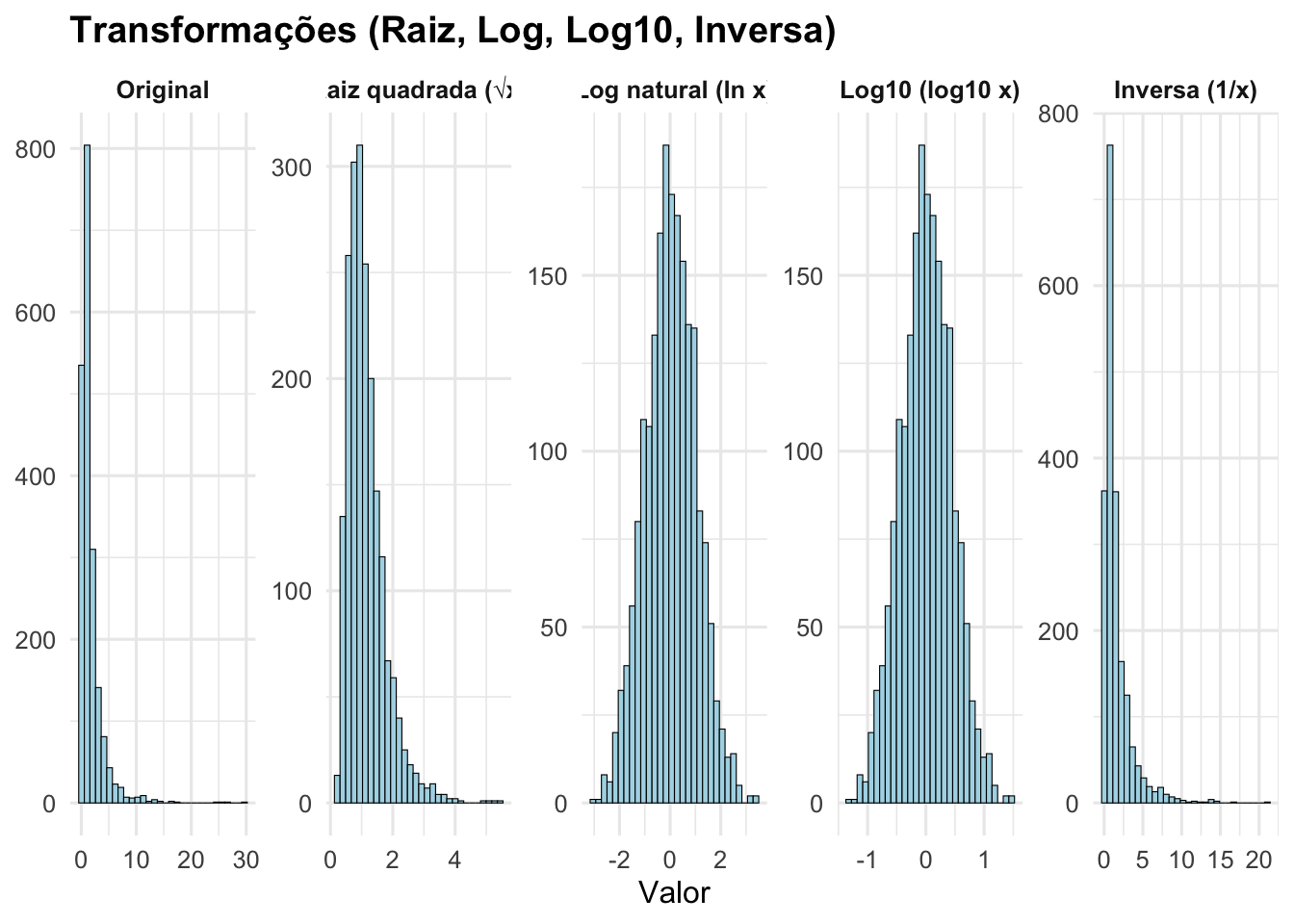
Figura 10.1: Transformações de variáveis com assimetria à direita (Original, Raiz quadrada, Log natural, Log10, Inversa).

• Distribuições com assimetria à esquerda: reflexão e raiz quadrada, reflexão e logaritmo natural, reflexão e logaritmo base 10, reflexão e transformação inversa.¹¹⁸

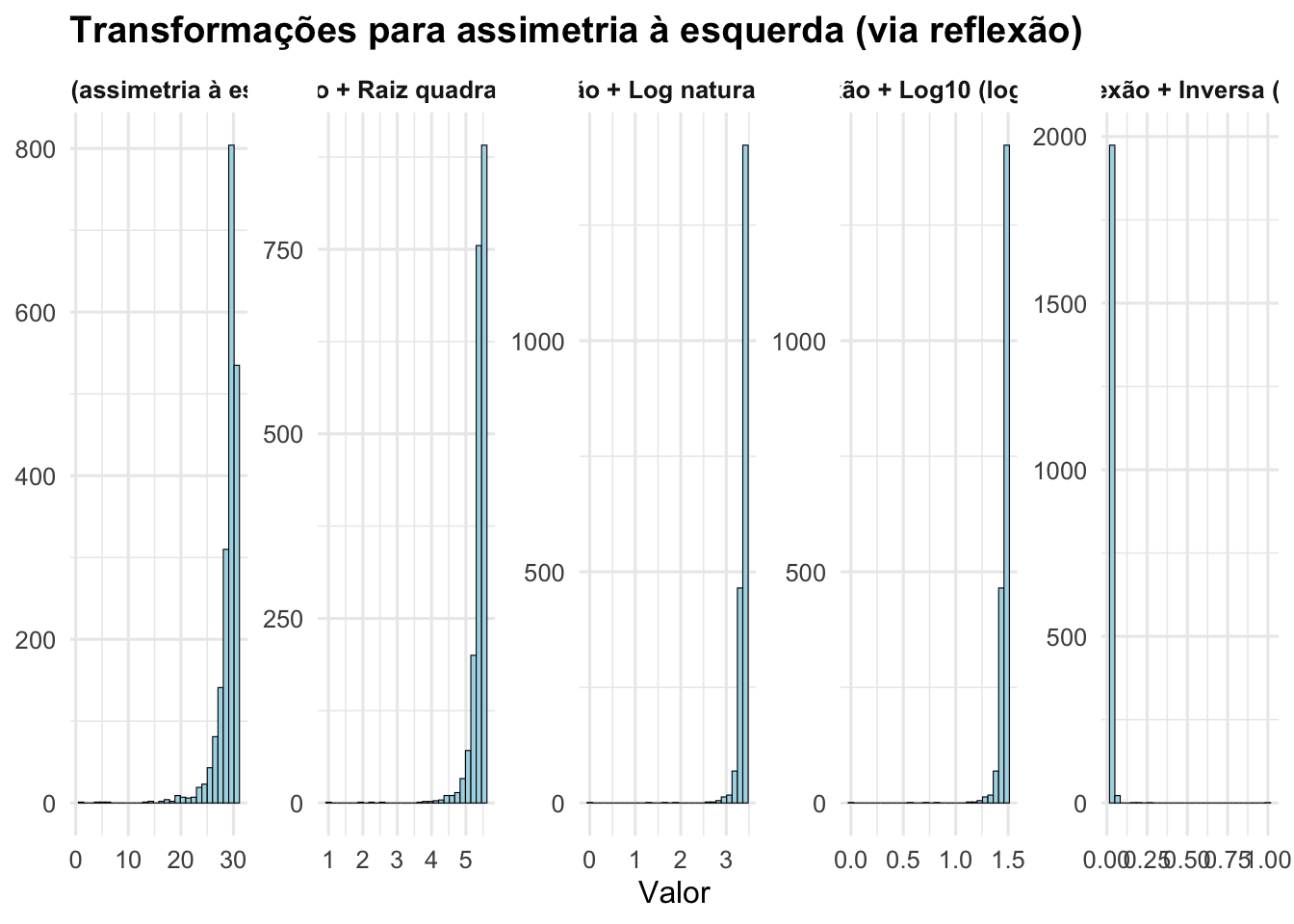
Figura 10.2: Transformações de variáveis com assimetria à esquerda (Original, Reflexão + Raiz quadrada, Reflexão + Log natural, Reflexão + Log10, Reflexão + Inversa).

• Transformação \(z\) de Fisher (10.1).[REF]

\[\begin{equation} \tag{10.1} Z = \frac{1}{2} \ln\left(\frac{1 + r}{1 - r}\right) \end{equation}\]

• Transformação de Box-Cox (10.2).¹¹⁹

\[\begin{equation} \tag{10.2} Y(\lambda) = \begin{cases} \frac{Y^{\lambda} - 1}{\lambda}, & \text{se } \lambda \neq 0 \\ \ln(Y), & \text{se } \lambda = 0 \end{cases} \end{equation}\]

• Transformação arco-seno (10.3).¹¹⁸

\[\begin{equation} \tag{10.3} Y' = \arcsin(\sqrt{Y}) \end{equation}\]

• Diferenciação.

• Categorização.

• Dicotomização.

O pacote MASS¹²⁰ fornece a função boxcox para executar a transformação de Box-Cox.¹¹⁹

10.3 Centralização de variáveis (centering)

10.3.1 O que é centralização?

• É uma transformação linear em que se subtrai a média da variável de cada observação. O objetivo é recentrar a variável em torno de zero, sem alterar a sua variabilidade.^REF?

10.3.2 Por que centralizar?

• Facilita a interpretação dos coeficientes de regressão, especialmente em modelos com termos de interação.^REF?

• Reduz a multicolinearidade entre variáveis e seus termos de interação ou polinomiais.^REF?

• Mantém a escala original (apenas desloca a média).^REF?

10.4 Padronização de variáveis

10.4.1 O que é padronização?

• Padronização é a transformação de uma variável contínua para uma escala comum, permitindo comparações entre variáveis medidas em diferentes unidades ou magnitudes.^REF?

10.4.2 Por que padronizar?

• Facilita a interpretação em análises multivariadas.^REF?

• Evita que variáveis em escalas maiores dominem os resultados de algoritmos que dependem de distância.^REF?

• Melhora a comparabilidade entre estudos e bases de dados diferentes.^REF?

10.4.3 Quais são os métodos de padronização mais comuns?

• Escore-Z (Z-score) (10.4): subtrair a média e dividir pelo desvio-padrão.^REF?

\[\begin{equation} \tag{10.4} Z = \frac{X - \mu}{\sigma} \end{equation}\]

• Escala Min-Max (10.5): transformar para o intervalo [0,1].^REF?

\[\begin{equation} \tag{10.5} X_{norm} = \frac{X - X_{min}}{X_{max} - X_{min}} \end{equation}\]

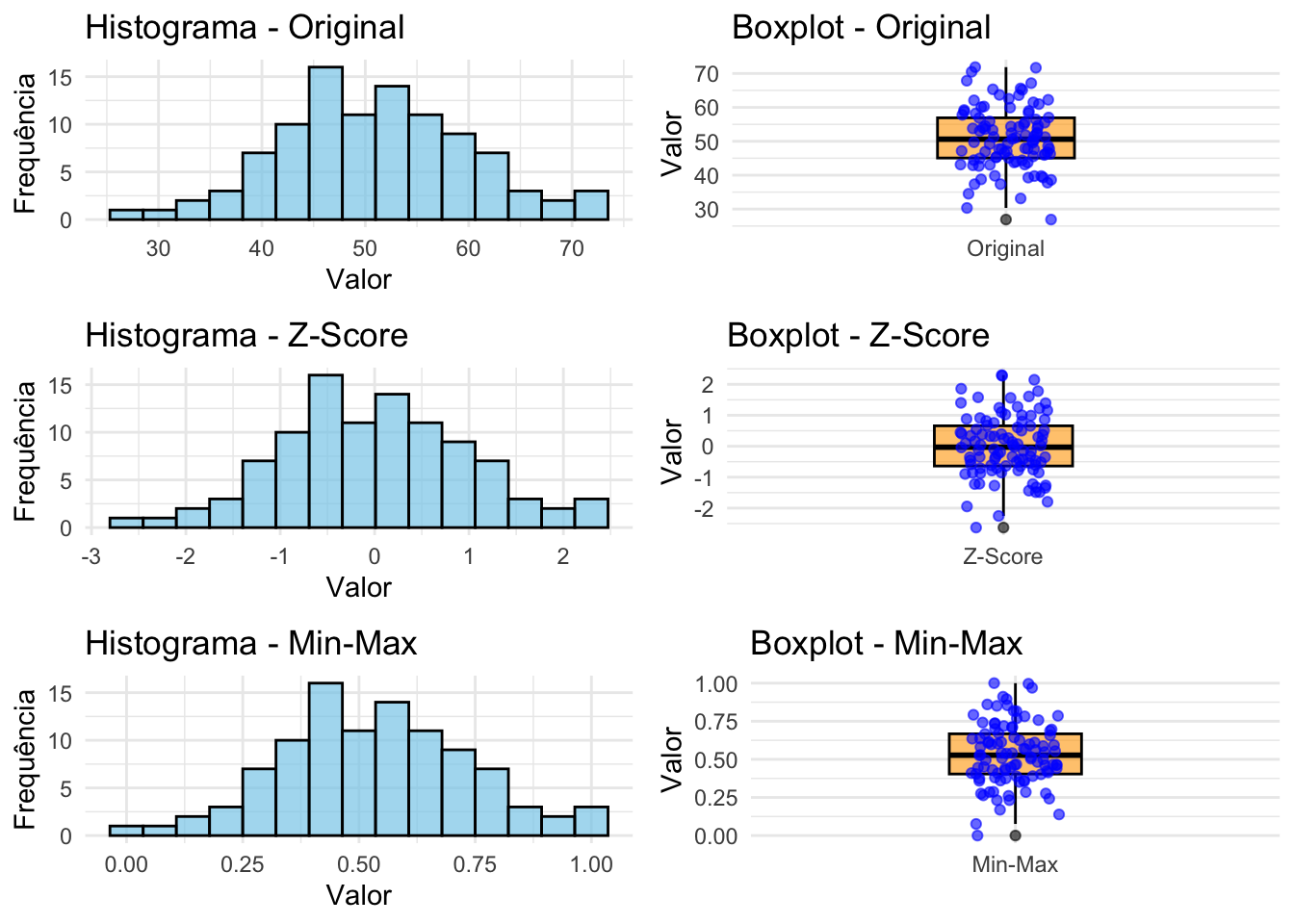
Figura 10.3: Comparação entre variáveis originais e padronizadas (Z-score e Min-Max).

10.4.4 Quais são as boas práticas de nomenclatura ao padronizar variáveis?

• Usar sufixos como _z ou _std para indicar padronização (altura_z, peso_std).^REF?

• Documentar no dicionário de dados como cada variável foi transformada.^REF?

• Evitar substituir a variável original: manter sempre a versão bruta e a padronizada.^REF?

O pacote base⁵⁷ fornece a função scale para calcular automaticamente a padronização (média = 0, desvio padrão = 1).

10.5 Categorização de variáveis contínuas

10.5.1 O que é categorização de uma variável?

• .^REF?

10.5.2 Por que não é recomendado categorizar variáveis contínuas?

• Nenhum dos argumentos usados para defender a categorização de variáveis se sustenta sob uma análise técnica rigorosa.¹²¹

• Categorizar variáveis não é necessário para conduzir análises estatísticas. Ao invés de categorizar, priorize as variáveis contínuas.^122–124

• Em geral, não existe uma justificativa racional (plausibilidade biológica) para assumir que as categorias artificiais subjacentes existam.^122–124

• Caso exista um ponto de corte ou limiar verdadeiro que discrimine três ou mais grupos independentes, identificar tal ponto de corte ainda é um desafio.¹²⁵

• Categorização de variáveis contínuas aumenta a quantidade de testes de hipótese para comparações pareadas entre os quantis, inflando, portanto, o erro tipo I.¹²⁶

• Categorização de variáveis contínuas requer uma função teórica que pressupõe a homogeneidade da variável dentro dos grupos, levando tanto a uma perda de poder como a uma estimativa imprecisa.¹²⁶

• Categorização de variáveis contínuas pode dificultar a comparação de resultados entre estudos devido aos pontos de corte baseados em dados de um banco usados para definir as categorias.¹²⁶

O pacote questionr¹²⁷ fornece a função irec para executar uma interface interativa para codificação de variáveis categóricas.

10.5.3 Quais são as alternativas à categorização de variáveis contínuas?

• Análise com os dados das variáveis na escala de medida original.¹²¹

• Análise com modelos de regressão com pesos locais (lowess) tais como splines e polinômios fracionais.¹²¹

10.6 Dicotomização de variáveis contínuas

10.6.1 O que são variáveis dicotômicas?

• Variáveis dicotômicas (ou binárias) podem representar categorias naturais tipo “presente/ausente”, “sim/não”.^REF?

• Variáveis dicotômicas podem representar categorias fictícias, criadas a partir de variáveis multinominais, em que cada nível é convertido em uma variável dicotômica indicatoda (dummy).^REF?

• Dicotomização é considerado um artefato da análise de dados, uma vez que é realizada após a coleta de dados.¹²⁸

• Geralmente são representadas por “1” (presente, sucesso) e “0” (ausente, falha).^REF?

10.6.2 Quais argumentos são usados para defender a categorização ou dicotomização de variáveis contínuas?

• O argumento principal para dicotomização de variáveis é que tal procedimento facilita e simplifica a apresentação dos resultados, principalmente para o público em geral.¹¹⁷

• Os pesquisadores não conhecem as consequências estatísticas da dicotomização.¹²¹

• Os pesquisadores não conhecem os métodos adequados de análise não-paramétrica, não-linear e robusta.¹²¹

• As categorias representam características existentes dos participantes da pesquisa, de modo que as análises devam ser feitas por grupos e não por indivíduos.¹²¹

• A confiabilidade da(s) variável(eis) medida(s) é baixa e, portanto, categorizar os participantes resultaria em uma medida mais confiável.¹²¹

10.6.3 Por que não é recomendado dicotomizar variáveis contínuas?

• Nenhum dos argumentos usados para defender a dicotomização de variáveis se sustenta sob uma análise técnica rigorosa.¹²¹

• Dicotomizar variáveis não é necessário para conduzir análises estatísticas. Ao invés de dicotomizar, priorize as variáveis contínuas.^122–124

• Em geral, não existe uma justificativa racional (plausibilidade biológica) para assumir que as categorias artificiais subjacentes existam.^122–124

• Dicotomização causa perda de informação e consequentemente perda de poder estatístico para detectar efeitos.^121,122

• Dicotomização também classifica indivíduos com valores próximos na variável contínua como indivíduos em pontos opostos e extremos, artificialmente sugerindo que são muito diferentes.¹²²

• Dicotomização pode diminuir a variabilidade das variáveis.¹²²

• Dicotomização pode ocultar não-linearidades presentes na variável contínua.^121,122

• A média ou a mediana, embora amplamente utilizadas, não são bons parâmetros para dicotomizar variáveis.^117,122

• Caso exista um ponto de corte ou limiar verdadeiro que discrimine dois grupos independentes, identificar tal ponto de corte ainda é um desafio.¹²⁵

10.6.4 Quais cenários legitimam a dicotomização das variáveis contínuas?

• Quando existem dados e/ou análises que suportem a existência — não apenas a suposição ou teorização — de categorias com um ponto de corte claro e com significado entre elas.¹²¹

• Quando a distribuição da variável contínua é muito assimétrica, de modo que uma grande quantidade de observações está em um dos extremos da escala.¹²¹

10.6.5 Quais métodos são usados para dicotomizar variáveis contínuas?

• Em termos de tabelas de contingência 2x2, os seguintes métodos permitem¹²⁵ a identificação do limiar verdadeiro:

  • Youden.¹²⁹

  • Gini Index.¹³⁰

  • Estatística qui-quadrado (\(\chi^2\)).¹³¹

  • Risco relativo (\(RR\)).¹³²

  • Kappa (\(\kappa\)).¹³³.

10.7 Representação de variáveis categóricas

10.7.1 O que são variáveis indicadoras (dummy variables)?

• Variáveis indicadoras são variáveis dicotômicas criadas a partir dos níveis de um fator.^REF?

• Cada variável indicadora assume o valor \(1\) quando a observação pertence àquela categoria e \(0\) caso contrário.^REF?

• Variáveis indicadoras não representam magnitude ou ordem, apenas a presença ou ausência de uma categoria.^REF?

Tabela 10.1: Tabela de variáveis indicadoras (dummy variables) criadas a partir de variáveis categóricas Sexo e Grupo.

ID	Sexo	Grupo	Sexo_Feminino	Grupo_TratA	Grupo_TratB
1	Masculino	Tratamento A	1	1	0
2	Masculino	Controle	1	0	0
3	Masculino	Tratamento A	1	1	0
4	Feminino	Tratamento B	0	0	1
5	Masculino	Controle	1	0	0
6	Feminino	Tratamento B	0	0	1
7	Feminino	Tratamento B	0	0	1
8	Feminino	Controle	0	0	0
9	Masculino	Controle	1	0	0
10	Masculino	Controle	1	0	0
11	Feminino	Controle	0	0	0
12	Feminino	Tratamento B	0	0	1

O pacote stats¹³⁴ fornece a função model.matrix para expandir variáveis categóricas em variáveis indicadoras.

10.7.2 Por que variáveis indicadoras são importantes?

• Permitem a inclusão de fatores em modelos estatísticos.^REF?

• Tornam explícitas as comparações entre categorias.^REF?

• Garantem coerência matemática sem perder o significado conceitual das categorias.^REF?

10.7.3 Quantas variáveis indicadoras são necessárias para um fator?

• Um fator com k níveis é representado por \(k − 1\) variáveis indicadoras.^REF?

• O nível que não gera uma variável indicadora explícita é chamado de nível de referência.^REF?

10.7.4 O que é o nível de referência?

• O nível de referência é a categoria usada como base de comparação para as demais.^REF?

• Os coeficientes associados às variáveis indicadoras representam diferenças em relação a esse nível de referência.^REF?

10.7.5 Por que não se usam k variáveis indicadoras para \(k\) níveis?

• Utilizar \(k\) variáveis indicadoras gera redundância perfeita entre as variáveis.^REF?

• Essa redundância causa problemas de identificabilidade nos modelos, fenômeno conhecido como dummy trap.^REF?

10.7.6 Variáveis indicadoras são uma forma de dicotomização?

• Variáveis indicadoras são dicotômicas, mas não resultam da dicotomização de variáveis contínuas.^REF?

• Variáveis indicadoras são criadas a partir de variáveis categóricas multinominais, preservando toda a informação original do fator.^REF?

• Variáveis indicadoras não reduzem informação, enquanto a dicotomização de variáveis contínuas descarta informação por construção.^REF?

10.7.7 Variáveis indicadoras alteram os dados originais?

• Não. Variáveis indicadoras apenas representam os níveis do fator de forma numérica.^REF?

• A variável categórica original permanece intacta no conjunto de dados.^REF?

10.8 Fatores

10.8.1 O que são fatores?

• Fator é um sinônimo de variável categórica.^REF?

• Na modelagem, fator é sinônimo de variável preditora, em particular quando se refere à modelagem de efeitos fixos e aleatórios – os fatores (variáveis) são fatores fixos ou fatores aleatórios.^REF?

• Fatores são variáveis controladas pelos pesquisadores em um experimento para determinar seu efeito na(s) variável(ies) de resposta. Um fator pode assumir apenas um pequeno número de valores, conhecidos como níveis. Os fatores podem ser uma variável categórica ou baseados em uma variável contínua, mas usam apenas um número limitado de valores escolhidos pelos experimentadores.^REF?

O pacote base⁵⁷ fornece a função as.factor para converter uma variável em fator.

10.8.2 O que são níveis de um fator?

• Níveis de um fator são as possíveis categorias que descrevem um fator.^REF?

O pacote base⁵⁷ fornece as funções levels e nlevels para listar os níveis e a quantidade deles em um fator.

Citar como:
Ferreira, Arthur de Sá. Ciência com R: Perguntas e respostas para pesquisadores e analistas de dados. Rio de Janeiro: 1a edição,

Referências

57.

R Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2023. https://www.R-project.org/.

110.

Altman DG, Bland JM. Statistics notes Variables and parameters. BMJ. 1999;318(7199):1667–1667. doi:10.1136/bmj.318.7199.1667

111.

Vetter TR. Fundamentals of Research Data and Variables. Anesthesia & Analgesia. 2017;125(4):1375–1380. doi:10.1213/ane.0000000000002370

113.

Dettori JR, Norvell DC. The Anatomy of Data. Global Spine Journal. 2018;8(3):311–313. doi:10.1177/2192568217746998

114.

Kaliyadan F, Kulkarni V. Types of variables, descriptive statistics, and sample size. Indian Dermatology Online Journal. 2019;10(1):82. doi:10.4103/idoj.idoj_468_18

115.

Barkan H. Statistics in clinical research: Important considerations. Annals of Cardiac Anaesthesia. 2015;18(1):74. doi:10.4103/0971-9784.148325

116.

Bland JM, Altman DG. Statistics Notes: Transforming data. BMJ. 1996;312(7033):770–770. doi:10.1136/bmj.312.7033.770

117.

Fedorov V, Mannino F, Zhang R. Consequences of dichotomization. Pharmaceutical Statistics. 2009;8(1):50–61. doi:10.1002/pst.331

118.

Osborne J. Improving your data transformations: Applying the Box-Cox transformation. University of Massachusetts Amherst. 2010. doi:10.7275/QBPC-GK17

119.

Box GEP, Cox DR. An Analysis of Transformations. Journal of the Royal Statistical Society: Series B (Methodological). 1964;26(2):211–243. doi:10.1111/j.2517-6161.1964.tb00553.x

120.

Venables WN, Ripley BD. Modern Applied Statistics with S. Springer; 2002. https://www.stats.ox.ac.uk/pub/MASS4/.

121.

MacCallum RC, Zhang S, Preacher KJ, Rucker DD. On the practice of dichotomization of quantitative variables. Psychological Methods. 2002;7(1):19–40. doi:10.1037/1082-989x.7.1.19

122.

Altman DG, Royston P. The cost of dichotomising continuous variables. BMJ. 2006;332(7549):1080.1. doi:10.1136/bmj.332.7549.1080

124.

Collins GS, Ogundimu EO, Cook JA, Manach YL, Altman DG. Quantifying the impact of different approaches for handling continuous predictors on the performance of a prognostic model. Statistics in Medicine. 2016;35(23):4124–4135. doi:10.1002/sim.6986

125.

Nelson SLP, Ramakrishnan V, Nietert PJ, Kamen DL, Ramos PS, Wolf BJ. An evaluation of common methods for dichotomization of continuous variables to discriminate disease status. Communications in Statistics – Theory and Methods. 2017;46(21):10823–10834. doi:10.1080/03610926.2016.1248783

126.

Bennette C, Vickers A. Against quantiles: categorization of continuous variables in epidemiologic research, and its discontents. BMC Medical Research Methodology. 2012;12(1). doi:10.1186/1471-2288-12-21

127.

Barnier J, Briatte F, Larmarange J. questionr: Functions to Make Surveys Processing Easier.; 2023. https://CRAN.R-project.org/package=questionr.

128.

Aguinis H, Pierce CA, Culpepper SA. Scale Coarseness as a Methodological Artifact. Organizational Research Methods. 2008;12(4):623–652. doi:10.1177/1094428108318065

129.

Youden WJ. Index for rating diagnostic tests. Cancer. 1950;3(1):32–35. doi:10.1002/1097-0142(1950)3:1<32::aid-cncr2820030106>3.0.co;2-3

130.

Strobl C, Boulesteix AL, Augustin T. Unbiased split selection for classification trees based on the Gini Index. Computational Statistics & Data Analysis. 2007;52(1):483–501. doi:10.1016/j.csda.2006.12.030

131.

Pearson K. X. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 1900;50(302):157–175. doi:10.1080/14786440009463897

132.

Greiner M, Pfeiffer D, Smith RD. Principles and practical application of the receiver-operating characteristic analysis for diagnostic tests. Preventive Veterinary Medicine. 2000;45(1-2):23–41. doi:10.1016/s0167-5877(00)00115-x

133.

Fleiss JL. Measuring nominal scale agreement among many raters. Psychological Bulletin. 1971;76(5):378–382. doi:10.1037/h0031619

134.

R Core Team. R: A Language and Environment for Statistical Computing.; 2025. https://www.R-project.org/.