Capítulo 43 Redes neurais
43.1 Neurônios artificiais
43.1.1 O que são neurônios artificiais?
Neuronios artificiais (ou perceptrons) são modelos matemáticos que imitam o funcionamento dos neurônios biológicos, recebendo entradas, aplicando pesos e uma função de ativação para produzir uma saída.350–352
A equação geral de um neurônio artificial é dada por (43.1), onde \(x_i\) são as entradas, \(w_i\) os pesos, \(b\) o viés e \(\phi\) a função de ativação:
\[\begin{equation} \tag{43.1} y = \phi\left(\sum_{i=1}^{d} w_i\,x_i + b\right) \end{equation}\]
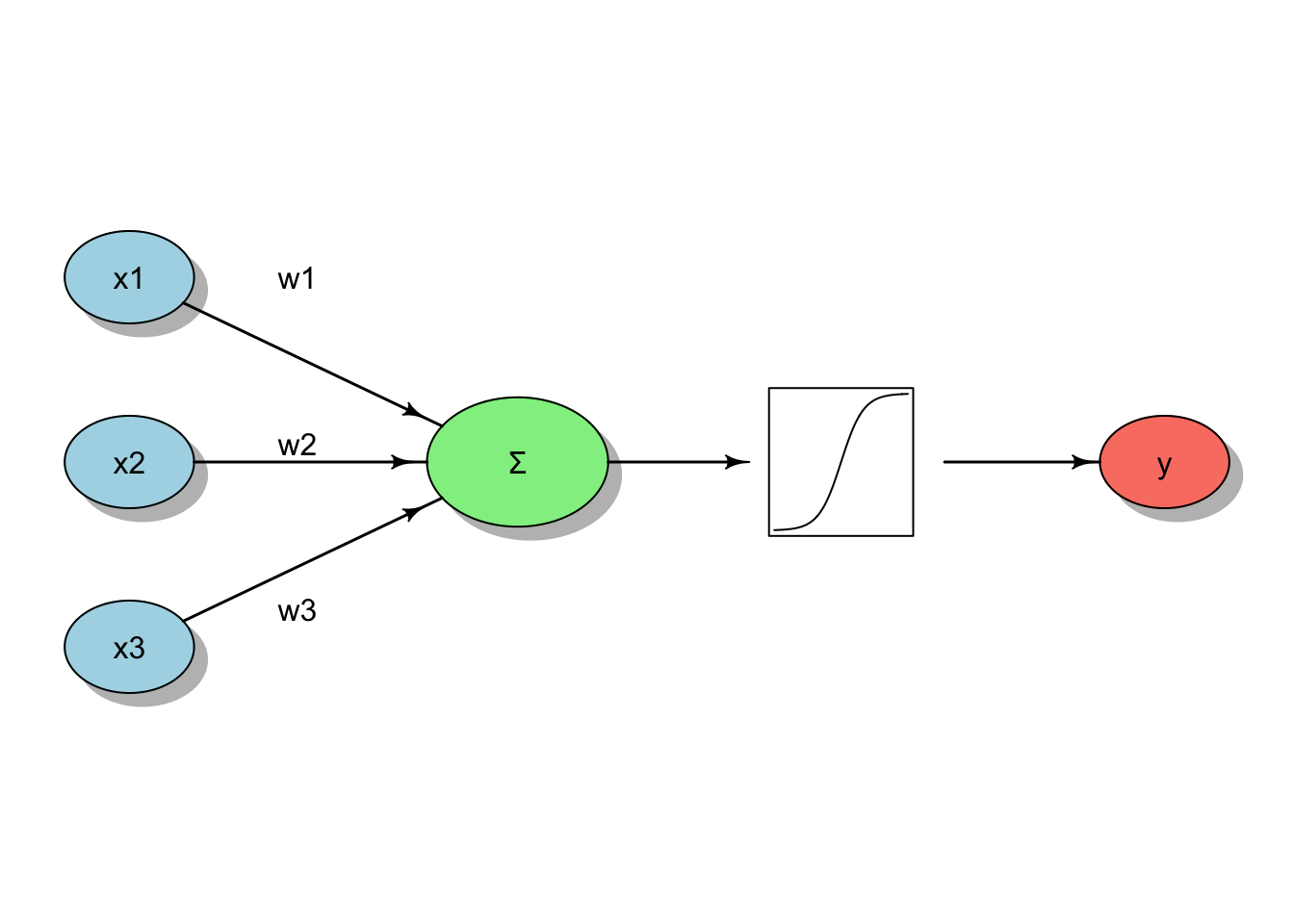
Figura 43.1: Representação esquemática de um neurônio computacional.
43.2 Rede neural artificial
43.2.1 O que é uma rede neural artificial?
- Redes neurais artificiais são modelos computacionais compostos por camadas de neurônios artificiais interconectados, nos quais cada camada aplica transformações lineares seguidas de funções não lineares, permitindo a aproximação de relações complexas entre variáveis de entrada e saída.REF?
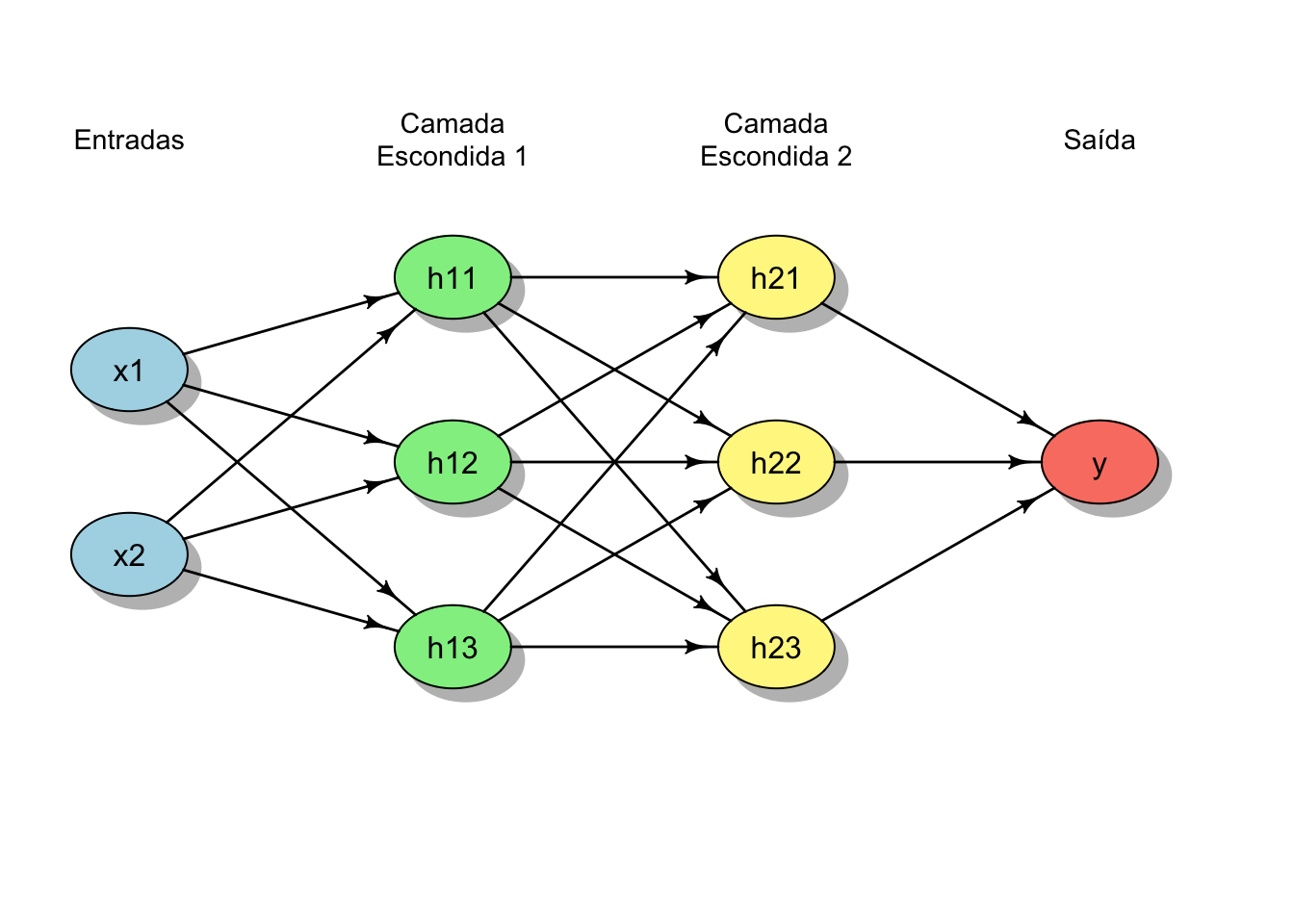
Figura 43.2: Representação esquemática de uma rede neural simples com camada de entrada e saída.
43.3 Funções de ativação
43.3.1 Quais são as funções de ativação mais comuns?
- As funções de ativação introduzem não-linearidades nas redes neurais, permitindo que aprendam padrões complexos, como sigmoide (43.2), tangente hiperbólica (43.3) e unidade linear retificada (ReLU) (43.4).REF?
\[\begin{equation} \tag{43.2} \sigma(z) = \frac{1}{1 + e^{-z}} \end{equation}\]
\[\begin{equation} \tag{43.3} \tanh(z) = \frac{e^{z} - e^{-z}}{e^{z} + e^{-z}} \end{equation}\]
\[\begin{equation} \tag{43.4} \operatorname{ReLU}(z) = \max(0, z) \end{equation}\]
Ao manter gradientes constantes na região positiva, a ReLU favorece estabilidade numérica e eficiência computacional em redes multicamadas.[REF?
Diferentemente das funções sigmoide e tangente hiperbólica, a ReLU preserva gradientes úteis em regiões amplas do espaço de entrada.REF?
Sem funções de ativação não lineares, uma rede neural profunda se reduz a um modelo linear equivalente.REF?
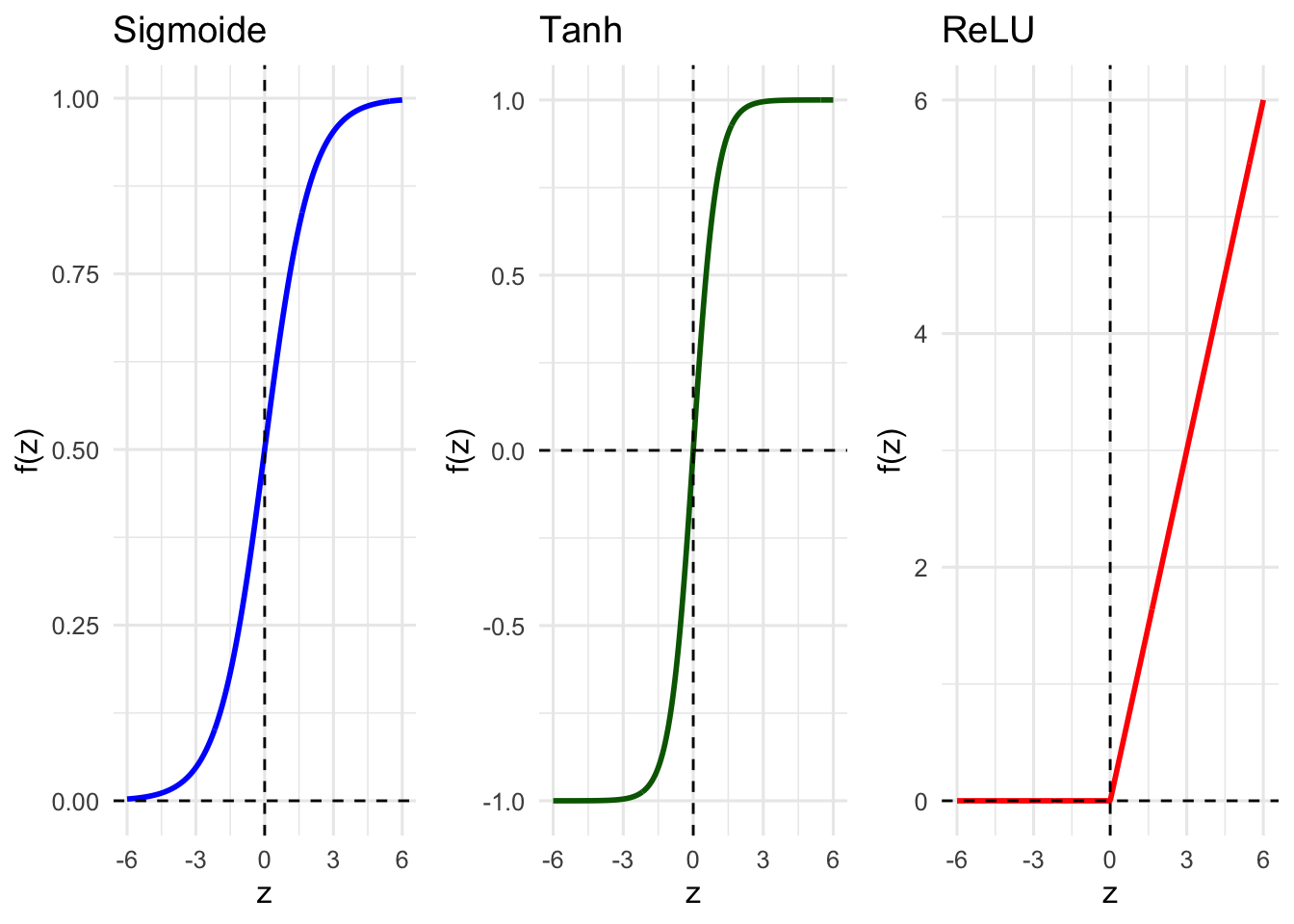
Figura 43.3: Gráficos das funções de ativação mais comuns.
43.4 Funções de perda
43.4.1 O que são funções de perda?
Funções de perda (loss functions) quantificam o erro cometido por um modelo ao comparar suas predições com os valores reais observados.REF?
Funções de perda definem formalmente o objetivo do aprendizado, indicando o que significa “errar pouco” ou “errar muito” em um problema específico.REF?
Durante o treinamento de modelos supervisionados, a função de perda orienta o ajuste dos parâmetros ao medir a discrepância entre saída prevista e desfecho verdadeiro.REF?
Em redes neurais, a minimização da função de perda é realizada por métodos iterativos baseados em gradientes, como a retropropagação do erro.REF?
A escolha da função de perda está intimamente ligada à natureza do problema (regressão, classificação, probabilidade, ranking) e influencia diretamente o espaço de decisão aprendido pelo modelo.REF?
43.4.2 Quais são as funções de perda mais comuns?
- Erro quadrático médio (Mean Squared Error, MSE (43.5)): Essa função penaliza erros grandes de forma mais severa, sendo adequada quando desvios elevados são indesejáveis e a média do erro quadrático é uma medida relevante de desempenho.REF?
\[\begin{equation} \tag{43.5} \mathcal{L}_{\mathrm{MSE}}(y, \hat{y}) = \frac{1}{n}\sum_{i=1}^{n} (y_i - \hat{y}_i)^2 \end{equation}\]
- Erro absoluto médio (Mean Absolute Error, MAE(43.6)): Essa função atribui peso linear aos erros, tornando-se mais robusta a valores extremos quando comparada ao erro quadrático médio.REF?
\[\begin{equation} \tag{43.6} \mathcal{L}_{\mathrm{MAE}}(y, \hat{y}) = \frac{1}{n}\sum_{i=1}^{n} \lvert y_i - \hat{y}_i \rvert \end{equation}\]
- Erro quadrático médio logarítmico (Mean Squared Logarithmic Error, MSLE (43.7)): Essa função enfatiza erros relativos, sendo particularmente útil quando diferenças proporcionais são mais relevantes do que diferenças absolutas.REF?
\[\begin{equation} \tag{43.7} \mathcal{L}_{\mathrm{MSLE}}(y, \hat{y}) = \frac{1}{n}\sum_{i=1}^{n} \left(\log(1+y_i) - \log(1+\hat{y}_i)\right)^2 \end{equation}\]
- Entropia cruzada binária (Binary Cross-Entropy, BCE (43.8)): Essa função mede a discrepância entre probabilidades previstas e observadas, sendo o critério padrão em problemas de classificação binária probabilística.
\[\begin{equation} \tag{43.8} \mathcal{L}_{\mathrm{BCE}}(y, \hat{y}) = -\frac{1}{n}\sum_{i=1}^{n} \left[ y_i \log(\hat{y}_i) + (1-y_i)\log(1-\hat{y}_i) \right] \end{equation}\]
- Entropia cruzada categórica (Categorical Cross-Entropy (43.9)): Essa função generaliza a entropia cruzada para múltiplas classes, penalizando previsões probabilísticas inconsistentes com a classe verdadeira.REF?
\[\begin{equation} \tag{43.9} \mathcal{L}_{\mathrm{CCE}}(y, \hat{y}) = -\frac{1}{n}\sum_{i=1}^{n} \sum_{k=1}^{K} y_{ik}\log(\hat{y}_{ik}) \end{equation}\]
- Função logística (log-verossimilhança negativa (43.10)): Essa função expressa o critério de máxima verossimilhança da regressão logística, conectando inferência estatística e aprendizado supervisionado.REF?
\[\begin{equation} \tag{43.10} \mathcal{L}_{\mathrm{log}}(y, \hat{p}) = -\sum_{i=1}^{n} \left[ y_i \log(\hat{p}_i) + (1-y_i)\log(1-\hat{p}_i) \right] \end{equation}\]
- Função hinge (Support Vector Machines (43.11)): Essa função busca maximizar a margem entre classes, penalizando classificações incorretas ou pouco confiantes em relação à fronteira de decisão.
\[\begin{equation} \tag{43.11} \mathcal{L}_{\mathrm{hinge}}(y, f(x)) = \frac{1}{n}\sum_{i=1}^{n} \max\left(0,\, 1 - y_i f(x_i)\right) \end{equation}\]
43.5 Treinamento de redes neurais
43.5.2 O que são os pesos em uma rede neural e por que eles são tratados como parâmetros do modelo?
- .REF?
43.5.9 Por que o uso de todo o conjunto de dados em cada atualização pode ser computacionalmente inviável?
- .REF?
43.6 Espaço de decisão
43.6.1 O que é espaço de decisão?
- O espaço de decisão é a região do espaço de entrada onde o modelo classifica as entradas em diferentes categorias. Ele é definido pelas fronteiras de decisão aprendidas pelo modelo durante o treinamento.REF?
43.6.2 Como ele é visualizado?
- O espaço de decisão pode ser visualizado graficamente, especialmente em problemas de classificação binária ou multiclasse, onde as regiões correspondem às classes previstas pelo modelo.REF?
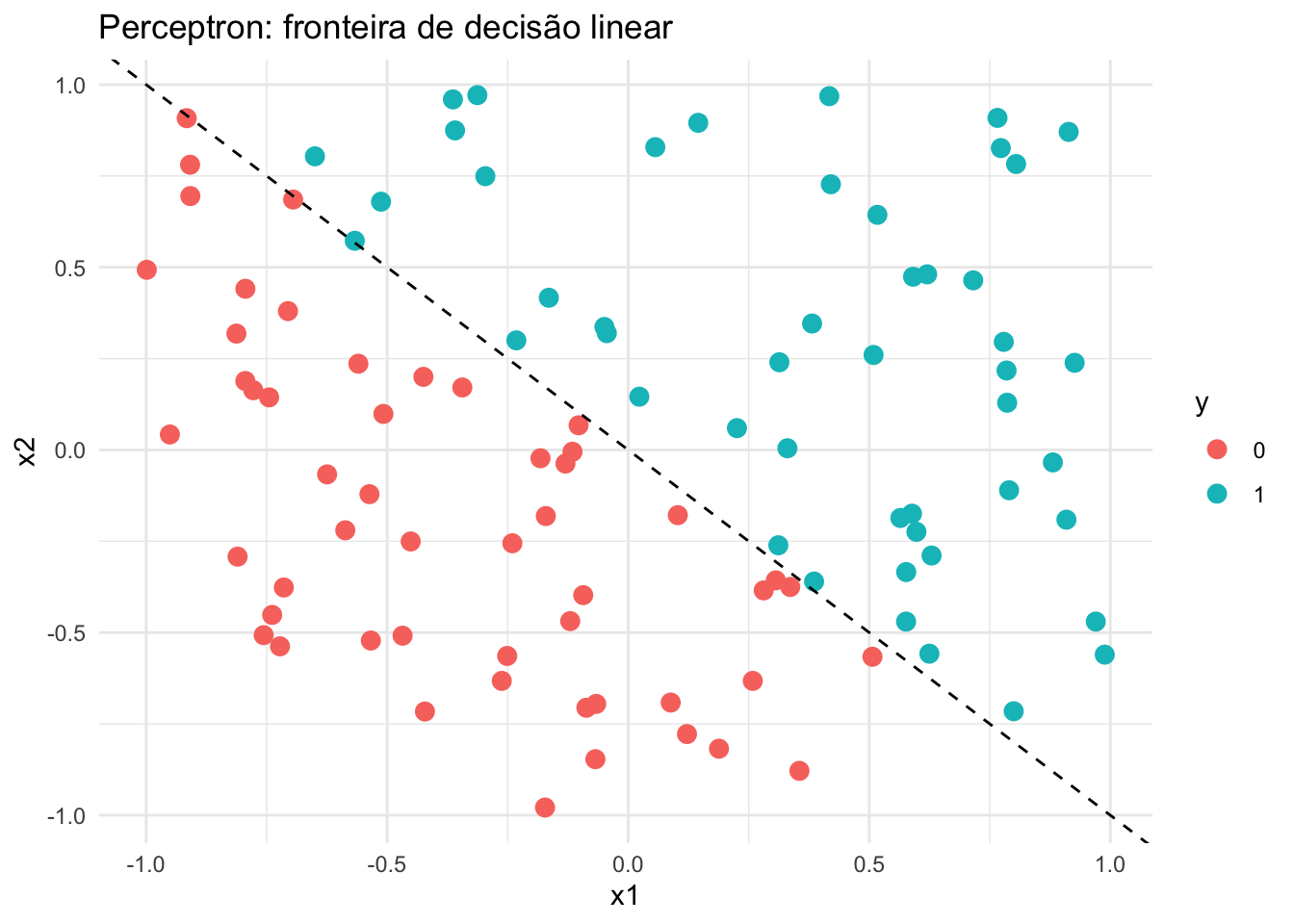
Figura 43.4: Espaço de decisão de um perceptron (regressão logística).
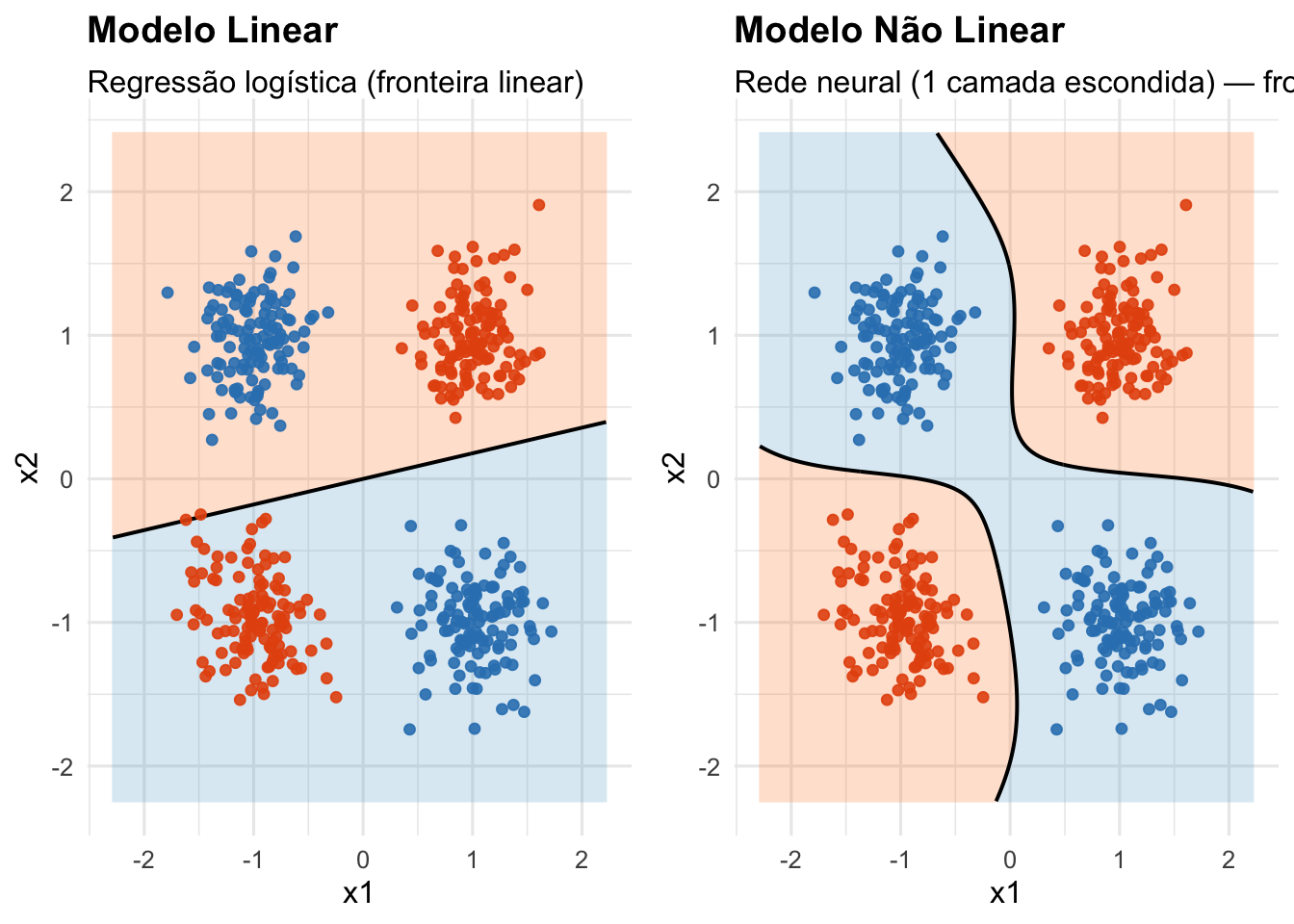
Figura 43.5: Comparação do espaço de decisão entre um modelo linear (regressão logística) e um modelo não linear (MLP).
43.7 Redes neurais multicamadas
43.7.1 O que são redes neurais multicamadas?
Redes neurais multicamadas são redes neurais artificiais que contêm uma ou mais camadas escondidas entre a camada de entrada e a camada de saída, permitindo a composição sucessiva de transformações não lineares e, consequentemente, maior capacidade de representação de funções complexas.REF?
Essa estrutura amplia o espaço de decisão do modelo sem exigir especificação explícita de interações ou transformações entre variáveis.REF?
À medida que a profundidade da rede aumenta, passa-se do ajuste de parâmetros para o aprendizado de representações internas dos dados, caracterizando um regime distinto de modelagem conhecido como aprendizado profundo.REF?
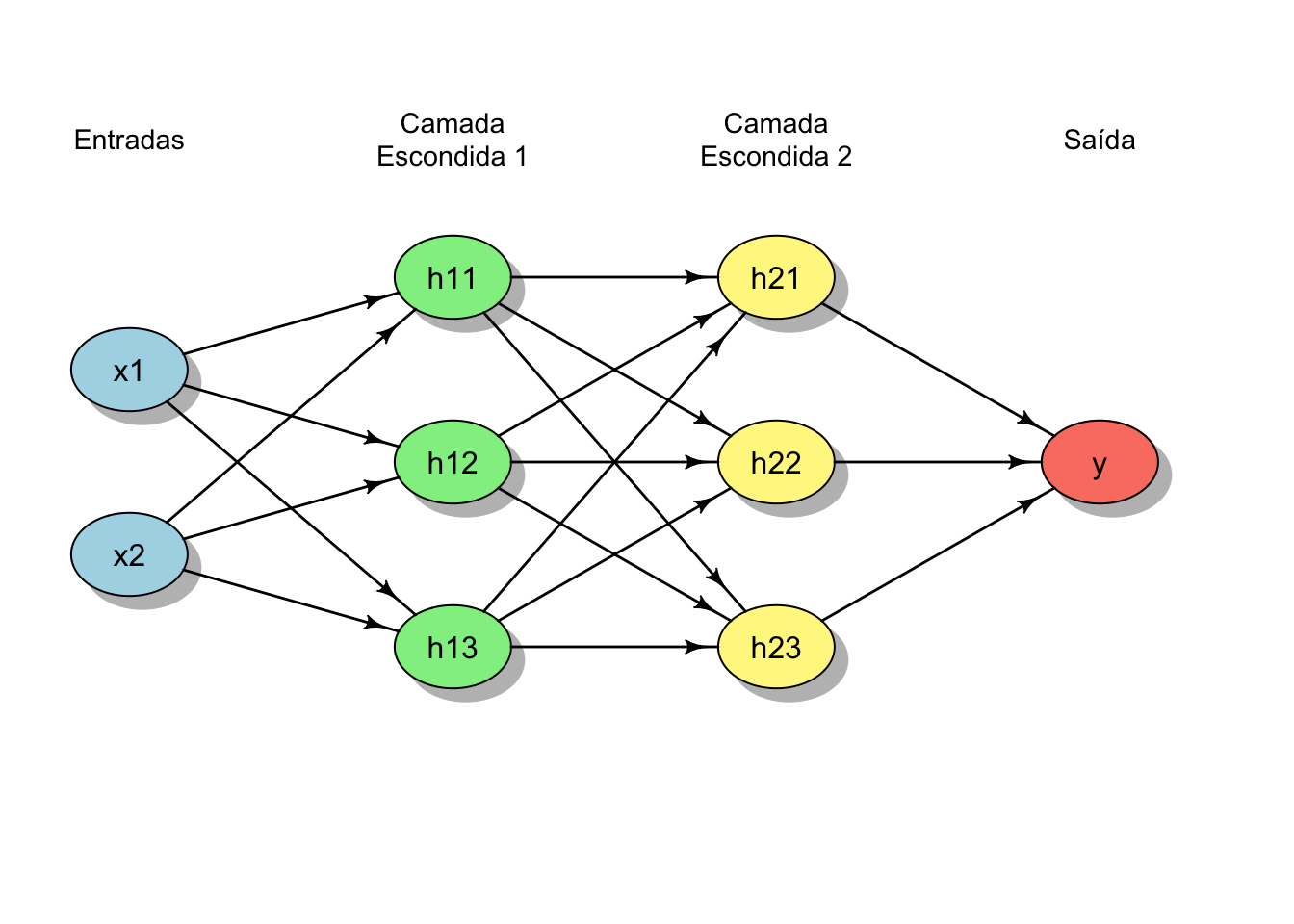
Figura 43.6: Representação esquemática de uma rede neural multicamadas com 2 camadas escondidas além das camadas de entrada e saída.
43.8 Redes neurais profundas
43.8.1 O que são redes neurais profundas?
- Redes neurais profundas (Deep Learning, DL) são redes neurais multicamadas com várias camadas escondidas, permitindo a modelagem de relações altamente complexas e abstratas nos dados.REF?
43.9 Redes neurais convolucionais (Convolutional Neural Networks)
43.9.1 O que são redes neurais convolucionais?
- Redes neurais convolucionais (Convolutional Neural Networks, CNNs) são arquiteturas de redes neurais especialmente projetadas para processar dados com estrutura de grade, como imagens, utilizando operações de convolução para extrair características locais e hierárquicas.REF?
43.9.2 O que é uma convolução?
- A convolução é uma operação matemática que combina duas funções para produzir uma terceira função, representando a sobreposição de uma função (o filtro ou kernel) sobre outra (a entrada), permitindo a extração de características locais em dados estruturados espacialmente.REF?
43.9.3 O que é um filtro convolucional?
- Um filtro convolucional (ou kernel) é uma pequena matriz de pesos utilizada na operação de convolução para detectar padrões específicos em dados de entrada, como bordas ou texturas em imagens, ao ser aplicada localmente sobre a entrada.REF?
43.9.4 Por que convoluções reduzem o número de parâmetros?
- Convoluções reduzem o número de parâmetros ao compartilhar pesos através de diferentes regiões da entrada, permitindo que o mesmo filtro seja aplicado em múltiplas posições, o que diminui a complexidade do modelo e melhora a eficiência computacional.REF?
Ferreira, Arthur de Sá. Ciência com R: Perguntas e respostas para pesquisadores e analistas de dados. Rio de Janeiro: 1a edição,