Capítulo 2 Pensamento estatístico
2.1 Unidade de análise
2.1.1 O que é unidade de análise?
A unidade de análise (ou unidade experimental) de pesquisas na área de saúde geralmente é o indivíduo.13
A unidade de análise também pode ser a instituição em estudos multicêntricos (ex.: hospitais, clínicas) ou um estudo publicado em meta-análise (ex.: ensaios clínicos).13
2.1.2 Por que identificar a unidade de análise de um estudo?
- É fundamental identificar corretamente a unidade de análise para evitar inflação do tamanho da amostra (ex.: medidas bilaterais resultando em o dobro de participantes), violações de suposições dos testes de hipótese (ex.: independência entre medidas e/ou unidade de análise) e resultados espúrios em testes de hipótese (ex.: P-valores menores que aqueles observados se a amostra não estivesse inflada).13,14
2.2 População
2.2.1 O que é população?
População — ou população-alvo — refere-se ao conjunto completo sobre o qual se pretende obter informações.15,16
População é metodologicamente delimitada pelos critérios de inclusão e exclusão do estudo.15
Em estudos observacionais, inicialmente as características geográficas e/ou demográficas, por exemplo, definem a população a ser estudada.15
Em estudos analíticos, a população é inicialmente definida pelos objetivos da pesquisa e, posteriormente, as observações são realizadas na amostra.15
2.2.2 O que é representatividade e por que ela importa?
Representatividade refere-se ao grau em que uma amostra reflete com fidelidade as características da população de referência.16
Quando a amostra contém menos indivíduos do que o número mínimo necessário, mas mantém a representatividade, a inferência estatística ainda é possível, embora possa haver redução da precisão e/ou do poder estatístico para detectar os efeitos.16
Amostras não representativas comprometem a validade da inferência estatística, mesmo quando o tamanho da amostra atende aos requisitos de poder da análise.16
2.3 Amostra
2.3.1 O que é amostra?
Em pesquisa científica, utilizam-se dados de uma amostra de participantes (ou outras unidades de análise) para realizar inferências sobre a população.17
2.3.2 Por que usar dados de amostras?
Estudos com amostras, em vez de censos, são preferíveis por diversas razões, dentre elas: questões éticas; limitações orçamentárias; desafios logísticos; restrição de tempo; e tamanho populacional desconhecido.16
Dados de uma amostra de tamanho suficiente e características representativas podem ser utilizados para inferência sobre uma população.8
Em geral, amostras de tamanhos maiores possuem médias mais próximas da média populacional e menores variâncias.8
2.4 Amostragem
2.4.1 O que é amostragem?
- Amostragem é o processo pelo qual se seleciona uma parte de uma população para constituir a amostra que será efetivamente estudada.16
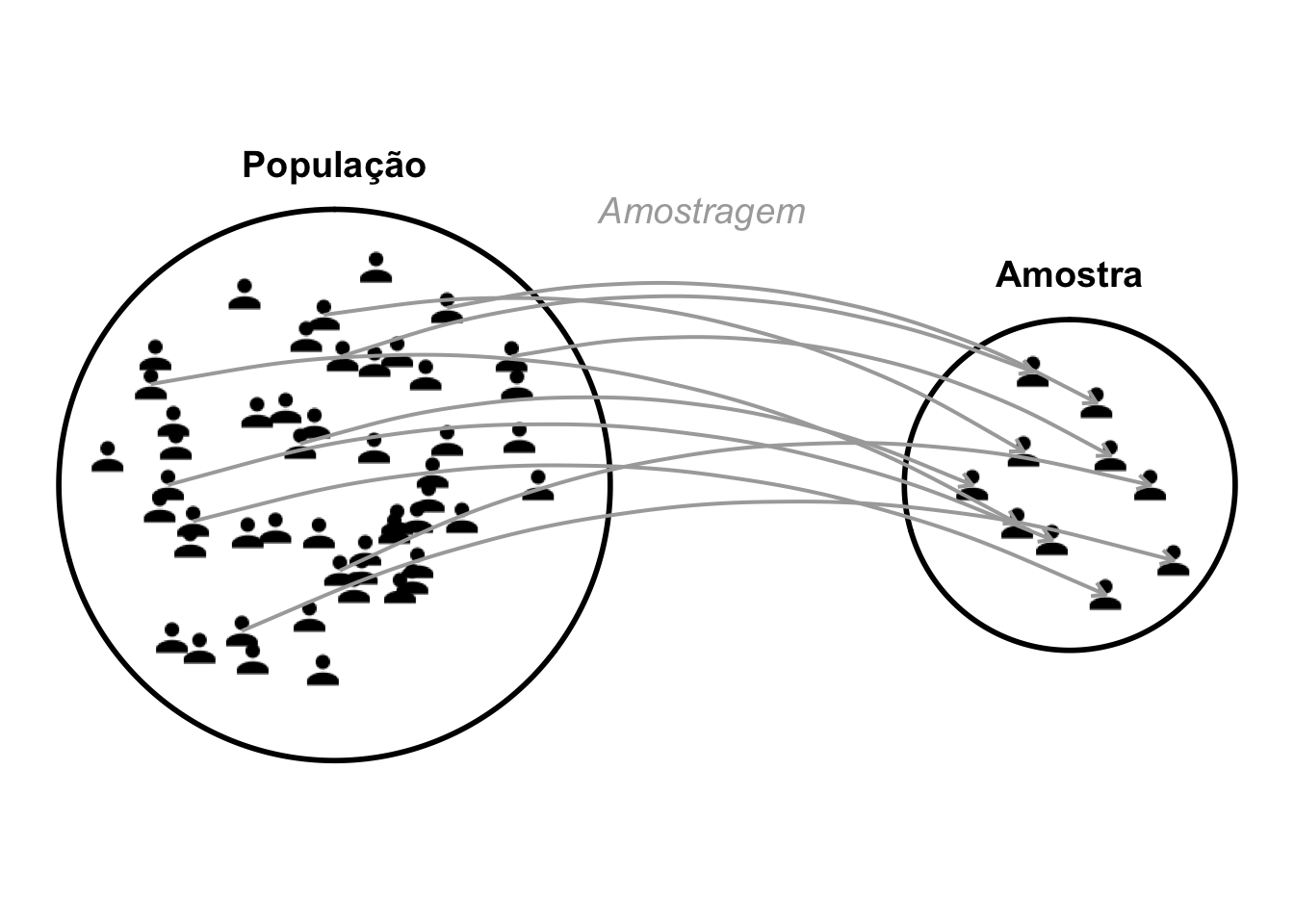
Figura 2.1: Representação esquemática da amostragem: seleção de uma população para a amostra.
2.4.2 Quais métodos de amostragem são usados para obter uma amostra da população?
O método de amostragem é geralmente definido pelas condições de viabilidade do estudo, no que diz respeito a acesso aos participantes, ao tempo de execução e aos custos envolvidos, entre outras.15
Não-probabilísticas ou intencionais:15,16
Bola de neve.
Conveniência.
Participantes encaminhados.
Proposital.
-
Simples.
Sistemática.
Multiestágio.
Estratificada.
Agregada.
2.4.3 O que é erro de amostragem?
- Erro de amostragem é a variação natural entre os resultados obtidos a partir de uma amostra e os resultados que seriam obtidos caso toda a população fosse examinada. Reflete o grau de incerteza inerente à generalização de uma amostra para a população.16
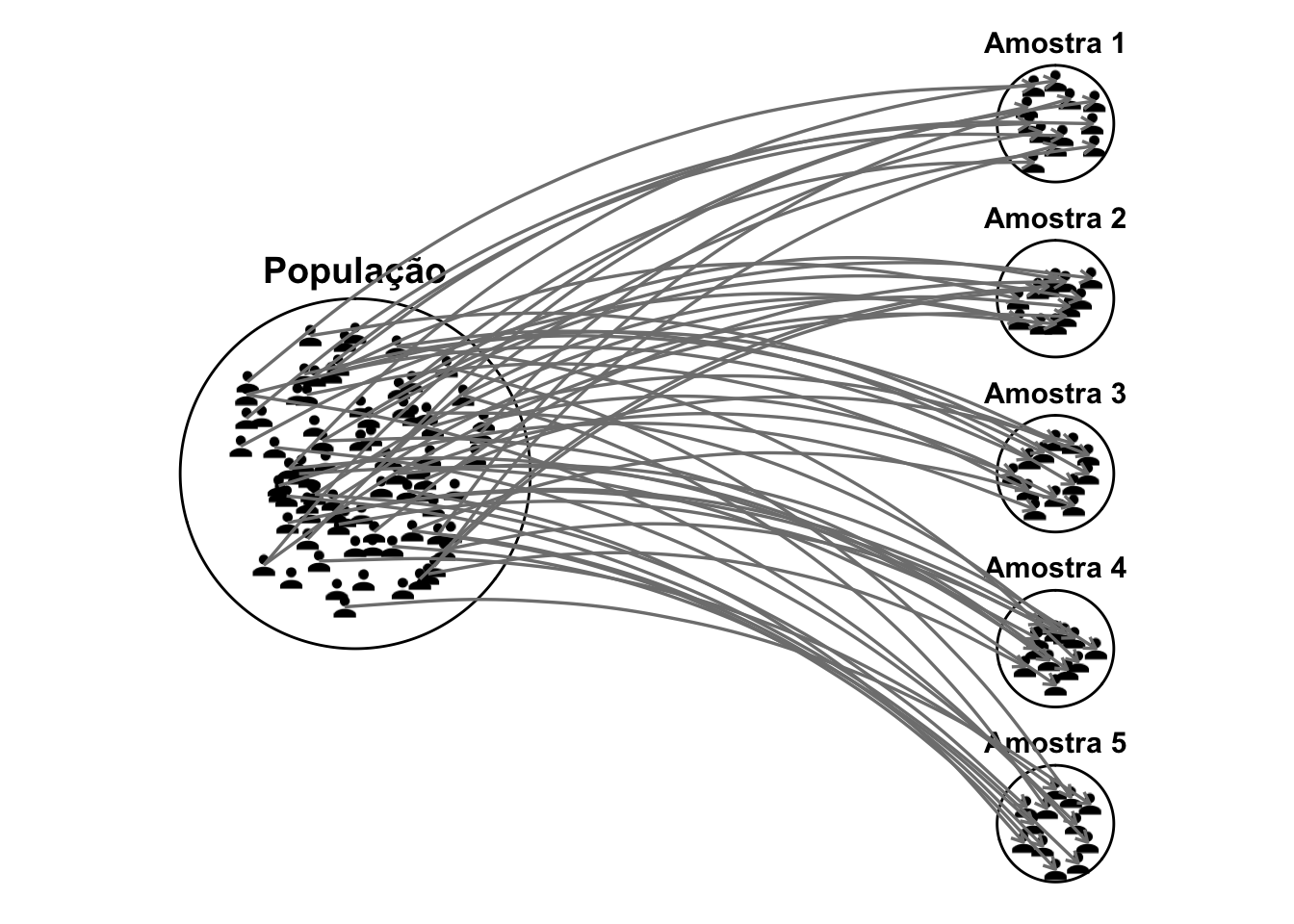
Figura 2.2: Representação esquemática do erro de amostragem: seleção de várias amostras independentes de uma população.
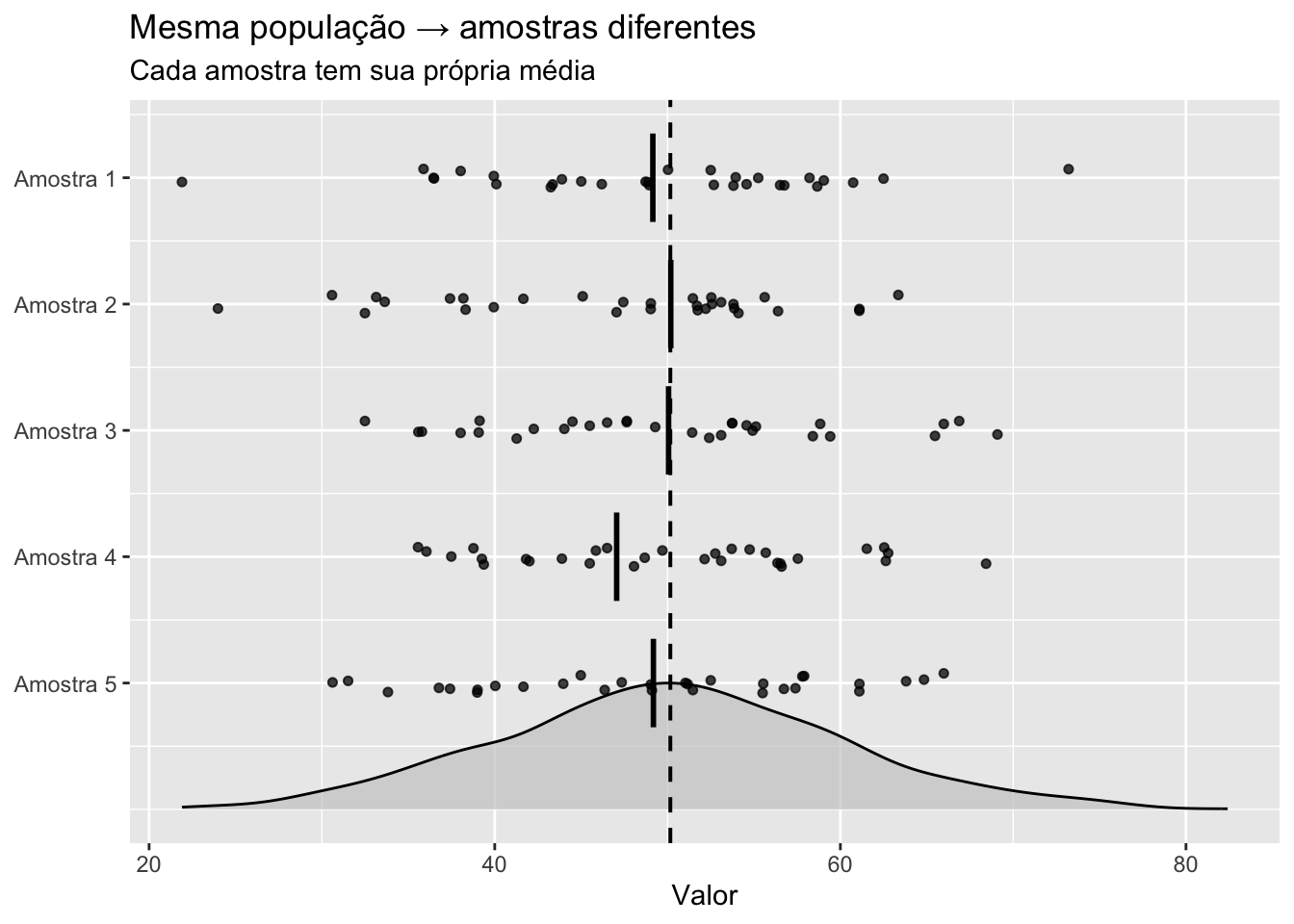
Figura 2.3: Representação esquemática da amostragem de uma população para a amostra.
2.5 Reamostragem
2.5.1 O que é reamostragem?
Reamostragem é um procedimento que cria vários conjuntos de dados sorteados a partir de um conjunto de dados real - a amostra da população - sem a necessidade de fazer suposições sobre os dados e suas distribuições.17
O procedimento é repetido várias vezes para usar a variabilidade dos resultados para obter um intervalo de confiança do parâmetro no nível de significância \(\alpha\) pré-estabelecido.17
2.5.2 Por que utilizar reamostragem?
Quando se dispõe de dados de apenas 1 amostra, as diversas suposições que são feitas podem não ser atingidas.17
Procedimentos de reamostragem produzem um conjunto de observações escolhidas aleatoriamente da amostra, igualmente representativo da população original.17
Procedimentos de reamostragem permitem estimar o erro-padrão e intervalos de confiança sem a necessidade de tais suposições, sendo, portanto, um conjunto de procedimentos não-paramétricos.17
2.5.3 Quais procedimentos de reamostragem podem ser realizados?
- Bootstrap: Cada iteração gera uma amostra bootstrap do mesmo tamanho do conjunto de dados original escolhendo aleatoriamente observações reais, uma de cada vez. Cada observação tem chances iguais de ser escolhida a cada vez, portanto, algumas observações serão escolhidas mais de uma vez e outras nem serão escolhidas.17
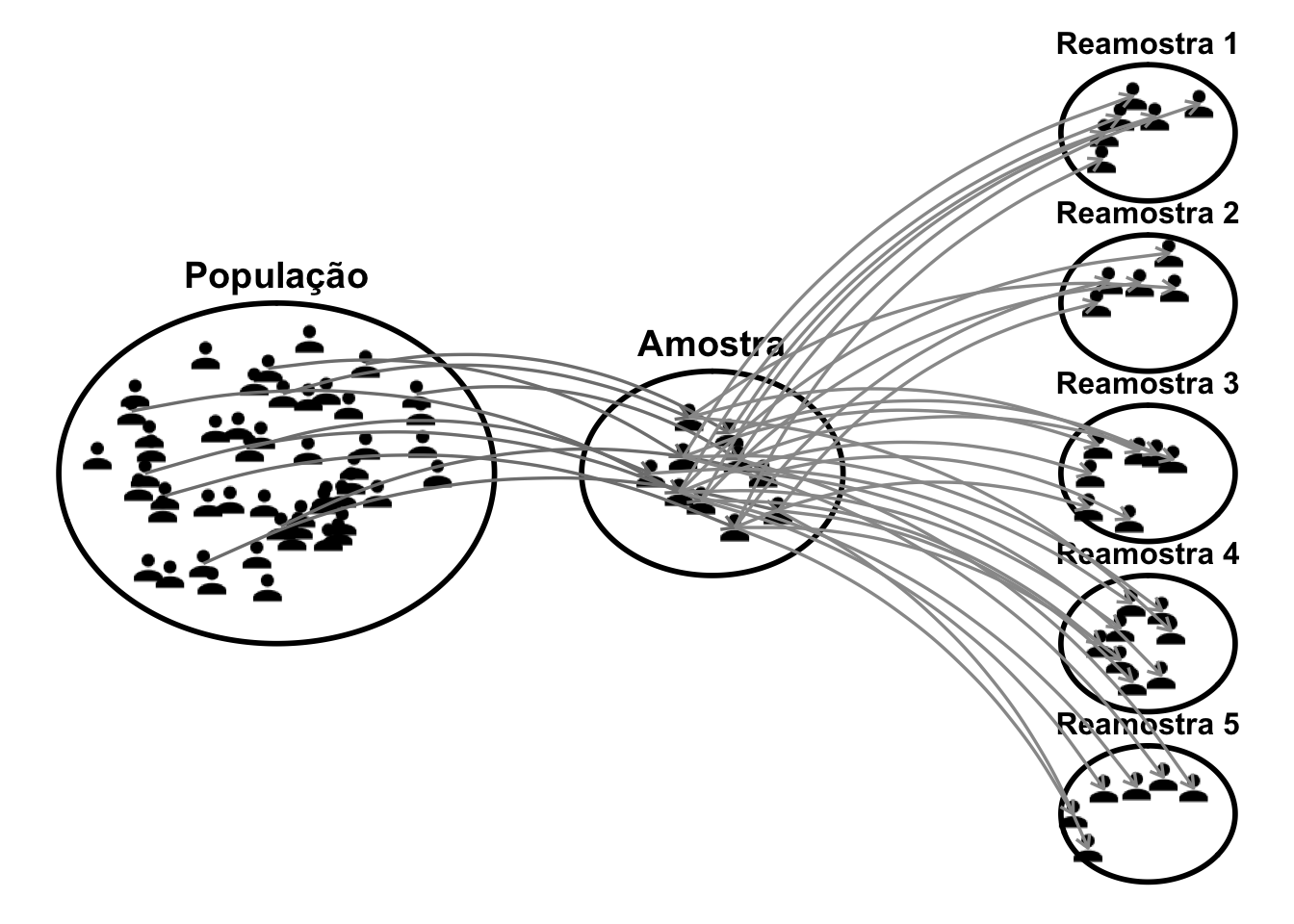
Figura 2.4: Representação esquemática da reamostragem de uma amostra.
2.6 Subamostragem
2.6.1 O que é subamostragem?
- .REF?
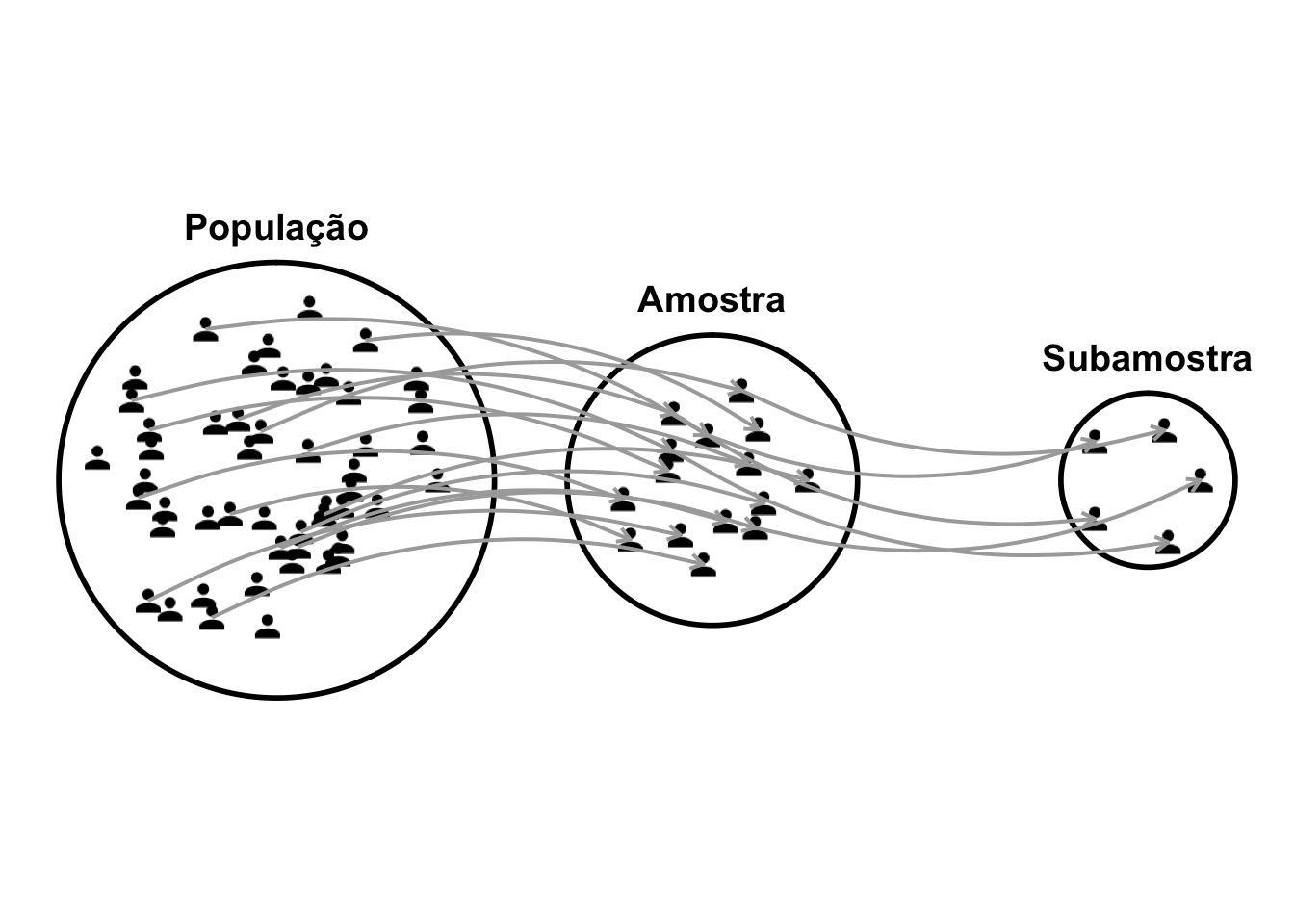
Figura 2.5: Representação esquemática da subamostragem de uma amostra.
2.7 Superamostragem
2.7.1 O que é superamostragem?
- .REF?
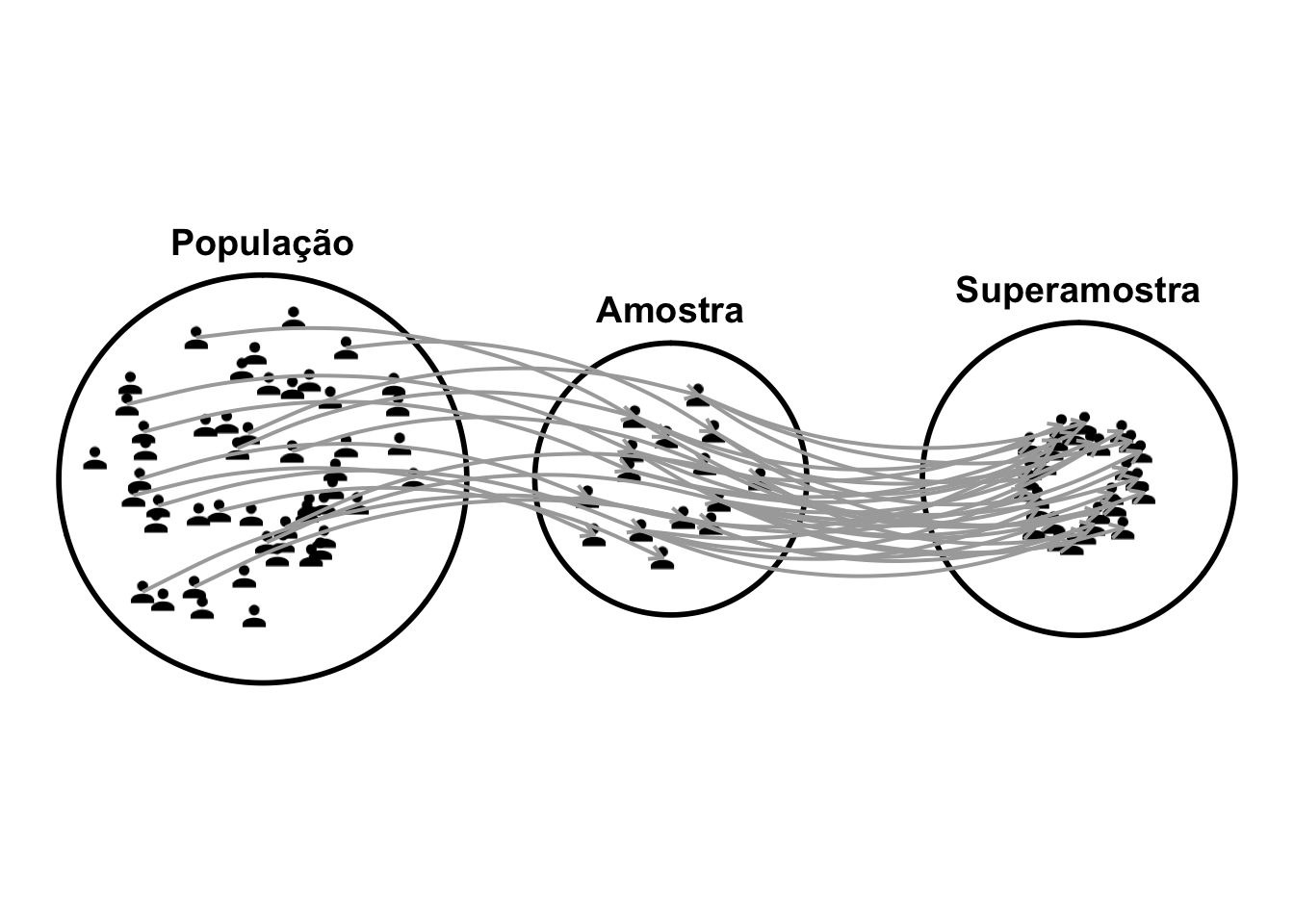
Figura 2.6: Representação esquemática da superamostragem de uma população.
Ferreira, Arthur de Sá. Ciência com R: Perguntas e respostas para pesquisadores e analistas de dados. Rio de Janeiro: 1a edição,