Capítulo 20 Análise descritiva
20.1 Análise descritiva
20.1.1 O que é análise descritiva?
- Análise descritiva é usada para compreendermos algum aspecto de um conjunto de dados, respondendo a perguntas do tipo “quando?”, “onde?”, “quem?”, “o quê?”, “como?” e “e daí?”.111,208
20.1.2 Como apresentar os resultados descritivos?
Variáveis categóricas: Reporte valores de frequência absoluta e relativa (n, percentual).209
Organização das tabelas: as variáveis são exibidas em linhas e os grupos são exibidos em colunas.209
Calcule percentagens para as colunas (isto é, entre grupos) e não entre linhas.209
Em caso de dados perdidos, não inclua uma linha com total de dados perdidos, pois distorce as proporções entre colunas e as análises de tabela de contingência. Indique no texto ou em uma coluna separada o total de dados perdidos por variável.209
20.2 Apresentação de resultados numéricos
20.2.1 O que são casas decimais?
O número de casas decimais refere-se à quantidade de dígitos que aparecem após a vírgula decimal.210,211
Para tamanhos de efeito: use 2–3 dígitos significativos.212
Para medidas de variabilidade (desvio-padrão/erro-padrão/intervalo de confian’;cça): use 1–2 dígitos significativos.212
20.2.2 O que são dígitos significativos?
O termo “dígitos significativos” é preferido a “algarismos significativos” ou “dígitos efetivos” e não se relaciona com significância estatística.210,211
O número de dígitos significativos é a soma total de dígitos, desconsiderando a vírgula decimal e os zeros à esquerda; os zeros à direita são considerados informativos, salvo exceções.210,211
20.2.3 Como arredondar dados numéricos?
Apresentar dados com quantidade excessiva de casas decimais pode dificultar a interpretação e induzir erroneamente uma precisão espúria.210,211
A precisão é determinada pelo grau de arredondamento aplicado, medido em casas decimais ou dígitos significativos.210,211
| Valor | Casas Decimais | Dígitos Significativos |
|---|---|---|
| 0,00789 | 5 | 0 |
| 0,0456 | 4 | 0 |
| 45,6 | 1 | 2 |
| 123,456 | 3 | 3 |
| 7890,0000 | 4 | 4 |
- O arredondamento também introduz erros, uma vez que aumenta a imprecisão (isto é, incerteza) em torno do valor original.210,211
| Valor | Casas Decimais | Dígitos Significativos | 2 Casas decimais [Margem de erro] | 1 Casa decimal [Margem de erro] | Sem casa decimal [Margem de erro] |
|---|---|---|---|---|---|
| 0,00789 | 5 | 0 | 0,01 [0,005, 0,015] | 0,0 [-0,05, 0,05] | 0 [-0,5, 0,5] |
| 0,0456 | 4 | 0 | 0,05 [0,045, 0,055] | 0,0 [-0,05, 0,05] | 0 [-0,5, 0,5] |
| 45,6 | 1 | 2 | 45,60 [45,595, 45,605] | 45,6 [45,55, 45,65] | 46 [45,5, 46,5] |
| 123,456 | 3 | 3 | 123,46 [123,455, 123,465] | 123,5 [123,45, 123,55] | 123 [122,5, 123,5] |
| 7890,0000 | 4 | 4 | 7890,00 [7889,995, 7890,005] | 7890,0 [7889,95, 7890,05] | 7890 [7889,5, 7890,5] |
A regra geral é utilizar 2 ou 3 dígitos significativos para tamanhos de efeito e 1 ou 2 dígitos significativos para medidas de variabilidade.211
Regra dos 3 dígitos significativos para proporção de risco: em média, o erro de arredondamento é menor que os 0,5% exigidos, de modo que três dígitos significativos são mais precisos do que o necessário.210
Regra dos 4 dígitos significativos para proporção de risco: divida a proporção de risco por quatro e arredonde para dois dígitos significativos e, em seguida, relate a proporção para esse número de casas decimais.210
20.3 Tabelas
20.3.1 Por que usar tabelas?
- Tabelas complementam o texto (e vice-versa), e podem apresentar os dados de modo mais acessível e informativo.213
20.3.2 Que informações incluir nas tabelas?
- Título ou legenda, uma síntese descritiva (geralmente por meio de parâmetros descritivos), intervalos de confiança e/ou P-valores conforme necessário para adequada interpretação.213,214
20.3.3 Quais são os tipos de tabelas?
Tabela de frequência: apresenta a quantidade de ocorrências (frequência absoluta e relativa) de cada categoria de uma variável; usada com variáveis qualitativas ou quantitativas discretas.REF?
Tabela de frequência agrupada: organiza dados contínuos em intervalos de classe (ex: faixas etárias) e mostra as frequências correspondentes.REF?
Tabela de contingência (ou tabela cruzada): cruza duas variáveis categóricas, permitindo observar possíveis associações entre elas.REF?
Tabela de medidas descritivas: resume variáveis quantitativas com estatísticas como média, mediana, desvio-padrão, mínimo, máximo e quartis.REF?
Tabela de comparação entre grupos: apresenta médias, desvios-padrão e ocasionalmente resultados de testes de inferência estatística para comparar dois ou mais grupos.REF?
Tabela de resultados de testes estatísticos: exibe valores de estatísticas de teste , P valores e intervalos de confiança; usada para mostrar inferências.REF?
Tabela de regressão (ou de modelos estatísticos): mostra os coeficientes de regressão, erros padrão, intervalos de confiança e P valores para cada variável de um modelo.REF?
Tabela de séries temporais ou longitudinais: organiza dados medidos em diferentes momentos no tempo, permitindo visualizar tendências ou variações longitudinais.REF?
O pacote gtsummary215 fornece a função tbl_summary para construção da ‘Tabela 1’ com dados descritivos.
O pacote flextable217 fornece as funções flextable, as_flextable e save_as_docx para criar e salvar tabelas formatadas em DOCX.
O pacote rempsyc218 fornece a função nice_table para criar tabelas formatadas.
20.3.4 Quais são os erros mais comuns de preenchimento de tabelas?
Erros tipográficos.219
Ausência de rótulos ou unidades nas variáveis.219
Relatar estatísticas incorretamente, tais como rotular variáveis contínuas como porcentagens.219
Estatísticas descritivas de tendência central (ex.: médias) relatadas sem a estatística de dispersão correspondente (ex.: desvio-padrão).219
Desvio-padrão nulo (\(\sigma=0\)).219
Valores porcentuais que não correspondem ao numerador dividido pelo denominador.219
20.4 Tabela 1
20.4.1 O que é a ‘Tabela 1’?
- A ‘Tabela 1’ descreve as características demográficas, sociais e clínicas da amostra, completa ou agrupada por algum fator, geralmente por meio de parâmetros de tendência central e dispersão.220,221
20.4.2 Qual a utilidade da ‘Tabela 1’?
Descrever (conhecer) as características da amostra e dos grupos sendo comparados, quando aplicável.221
Verificar aderência ao protocolo do estudo, incluindo critérios de inclusão/exclusão, tamanho da amostra e perdas amostrais.221
Permitir a replicação do estudo.221
Meta-analisar os dados junto a estudos similares.221
Avaliar a generalização (validade externa) das conclusões do estudo.221
20.4.3 O que é a falácia da ‘Tabela 1’?
Falácia da Tabela 1 ocorre pela interpretação errônea dos P-valores na comparação entre grupos, na linha de base, de um ensaio clínico aleatorizado.222
Não interprete P da linha de base em ensaios clínicos como “desequilíbrio” (falácia da Tabela 1). Mantenha P-valor apenas como descritivo (ou omita), enfatizando desenho e aleatorização.212
20.4.4 Como construir a ‘Tabela 1’?
- A Tabela 1 geralmente é utilizada para descrever as características da amostra estudada, possibilitando a análise de ameaças à validade interna e/ou externa ao estudo.181,223
O pacote gtsummary215 fornece a função tbl_summary para construção da ‘Tabela 1’ com dados descritivos.
| Características | N | Controle N = 1031 |
Intervenção N = 971 |
Valor-p2 |
|---|---|---|---|---|
| Sexo | 200 | 0.060 | ||
| F | 49 (48%) | 59 (61%) | ||
| M | 54 (52%) | 38 (39%) | ||
| Idade | 200 | 0.8 | ||
| Média (Desvio Padrão) | 61 (12) | 60 (12) | ||
| Mediana [Q1, Q3] | 61 [53, 69] | 60 [53, 69] | ||
| IMC | 200 | 0.2 | ||
| Média (Desvio Padrão) | 26.8 (3.7) | 27.5 (4.0) | ||
| Mediana [Q1, Q3] | 26.6 [24.5, 29.7] | 27.6 [25.6, 29.9] | ||
| 1 n (%) | ||||
| 2 Teste qui-quadrado de independência; Teste de soma de postos de Wilcoxon | ||||
20.5 Tabela 2
20.5.1 Qual a utilidade da ‘Tabela 2’?
- A Tabela 2 mostra associações ajustadas multivariadas com o resultado para variáveis resumidas na Tabela 1.220
20.5.2 O que é a falácia da ‘Tabela 2’?
A Tabela 2 pode induzir ao erro de interpretação pelas estimativas de efeitos para covariáveis do modelo também serem utilizados para controlar a confusão da exposição.220,224
Ao apresentar estimativas de efeito ajustadas para covariáveis juntamente com a estimativa de efeito ajustada para a exposição primária, a Tabela 2 sugere implicitamente que todas estas estimativas podem ser interpretadas de forma semelhante, se não de forma idêntica, como estimativa do efeito total.220,224
A falácia da Tabela 2 pode ser evitada limitando-se a tabela a estimativas das medidas primárias do efeito de exposição nos diferentes modelos, com as covariáveis secundárias de “ajuste” relatadas em uma nota de rodapé, juntamente com a forma como foram categorizadas ou modeladas.220
| Características |
Sem ajuste
|
Ajustado
|
||||
|---|---|---|---|---|---|---|
| OR | 95% IC | Valor-p | OR | 95% IC | Valor-p | |
| Grupo | ||||||
| Controle | — | — | — | — | ||
| Intervenção | 1.71 | 0.98, 3.02 | 0.061 | 1.70 | 0.97, 3.03 | 0.067 |
| Idade | 1.02 | 1.00, 1.05 | 0.087 | |||
| IMC | 1.05 | 0.97, 1.13 | 0.2 | |||
| Abreviações: IC = Intervalo de Confiança, OR = Razão de chances | ||||||
20.5.3 Como construir a ‘Tabela 2’?
- A Tabela 2 pode ser utilizada para apresentar estimativas de múltiplos efeitos ajustados de um mesmo modelo estatístico.220
| Características |
Sem ajuste
|
Ajustado
|
||||
|---|---|---|---|---|---|---|
| OR | 95% IC | Valor-p | OR | 95% IC | Valor-p | |
| Grupo | ||||||
| Controle | — | — | — | — | ||
| Intervenção | 1.71 | 0.98, 3.02 | 0.061 | 1.70 | 0.97, 3.03 | 0.067 |
| Abreviações: IC = Intervalo de Confiança, OR = Razão de chances | ||||||
| Nota. Modelo ajustado por Idade (contínua) e IMC (contínuo). Covariáveis são usadas apenas para controle de confusão e não devem ser interpretadas como efeitos causais (Falácia da Tabela 2). | ||||||
O pacote gtsummary215 fornece a função tbl_summary para construção da ‘Tabela 1’ com dados descritivos.
20.6 Visualização efetiva de dados
20.6.1 Por que começar pela mensagem antes do gráfico?
- A figura deve responder a uma pergunta clara (comparação? tendência? composição?) e isso orienta a escolha do tipo de gráfico, dados e anotações. Esboce a mensagem e a pergunta antes de abrir o software.225
20.6.2 Como escolher a geometria e “mostrar os dados”?
- Prefira geometrias que revelem distribuição/variabilidade (pontos, boxplots, violinos) em vez de médias sozinhas. Sempre que possível, exiba os dados brutos (pontos com jitter) junto da estatística-resumo.225
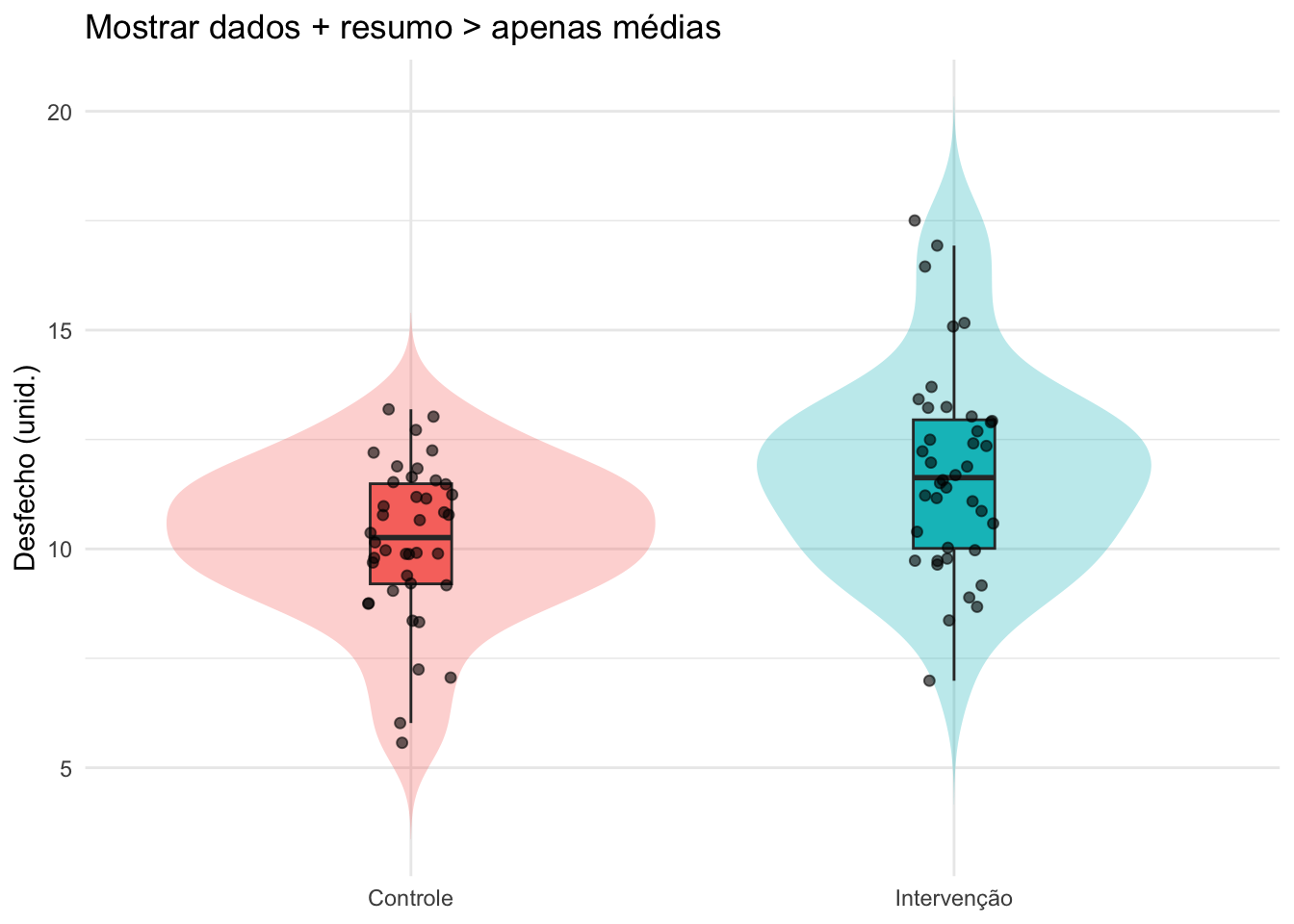
Figura 20.1: Exemplo de gráfico que mostra os dados brutos junto com um resumo estatístico (média e dispersão).
20.7 Gráficos
20.7.1 O que são gráficos?
- Gráficos são utilizados para apresentar dados (geralmente em grande quantidade) de modo mais intuitivo e fácil de compreender.226
20.7.2 O que torna um bom gráfico tão poderoso?
- “Não há ferramenta estatística tão poderosa quanto um gráfico bem escolhido”: gráficos ajudam a explorar dados, comunicar resultados e suportar decisões de forma clara e rápida.227
20.7.3 Que elementos incluir em gráficos?
- Título, eixos horizontal e vertical com respectivas unidades, escalas em intervalos representativos das variáveis, legenda com símbolos, síntese descritiva dos valores e respectiva margem de erro, conforme necessário para adequada interpretação.226
20.7.4 Para que servem as barras de erro em gráficos?
Barras de erro ajudam ao autor a apresentar as informações que descrevem os dados (por exemplo, em uma análise descritiva) ou sobre as inferências ou conclusões tomadas a partir de dados.186,187
Barras de erro mais longas representam mais imprecisão (maiores erros), enquanto barras mais curtas representam mais precisão na estimativa.187
Barras de erro descritivas geralmente apresentam a amplitude (mínimo-máximo) ou desvio-padrão.187
Barras de erro inferenciais geralmente apresentam o erro-padrão ou intervalo de confiança no nível de significância \(\alpha\) pré-estabelecido.186,187
Barras de erro com desvio-padrão são úteis para descrever a variabilidade dos dados, enquanto as barras de erro com erro padrão da média são úteis para descrever a precisão do parâmetro estimado (média) e sua relação com o tamanho da amostra.186
Barras de erro com intervalo de confiança são úteis para fornecer uma estimativa da incerteza da estimativa do parâmetro populacional.186
O comprimento das barras de erro sugere graficamente a imprecisão dos dados do estudo, uma vez que o valor verdadeiro da população pode estar em qualquer nível do intervalo da barra.187
De modo contraintuitivo, um espaço entre as barras não garante significância, nem a sobreposição a descarta—depende do tipo de barra.186
Para amostras pequenas é preferível apresentar os dados brutos, uma vez que as barras de erro não serão muito informativas.186
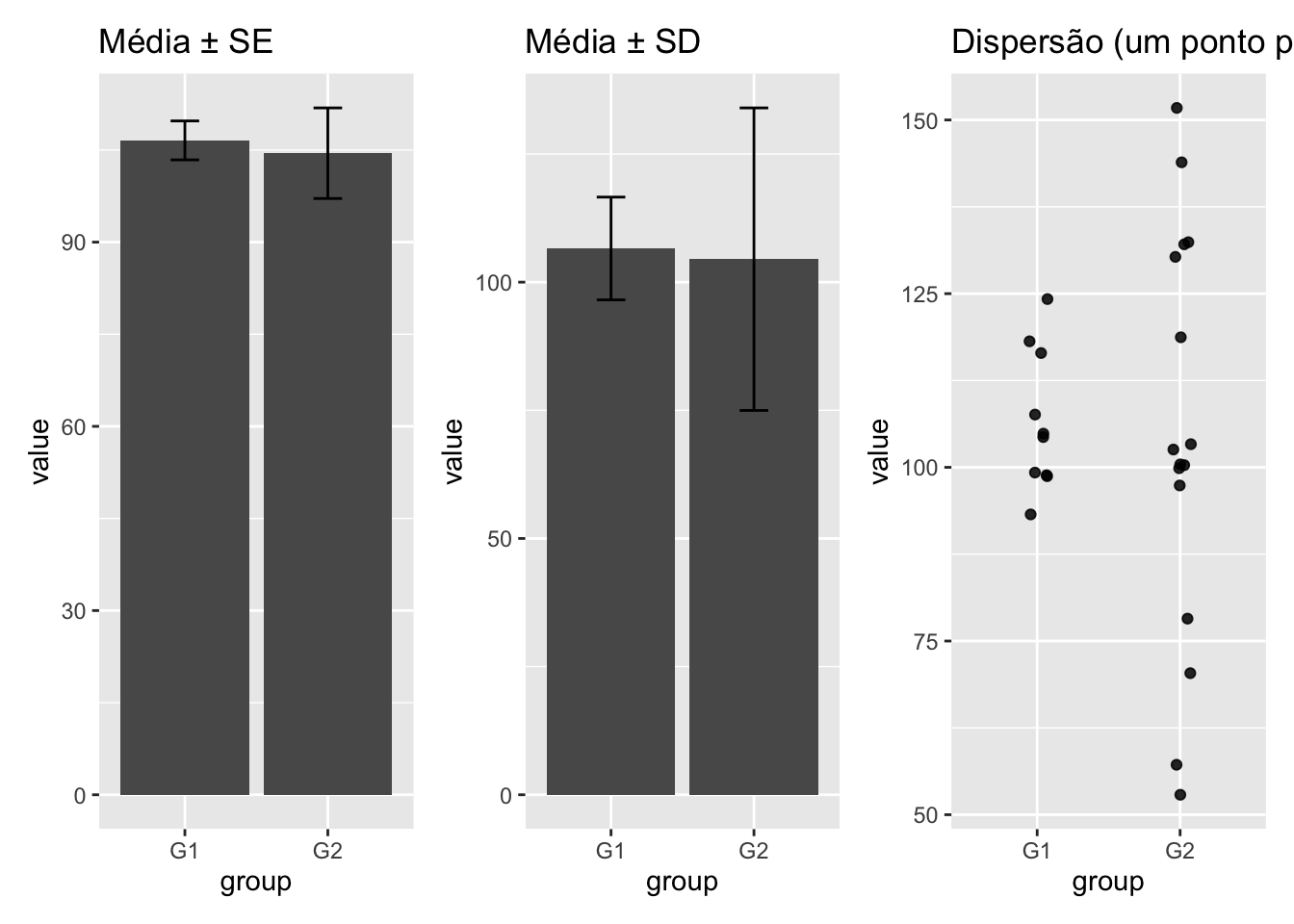
Figura 20.2: Exemplos de gráficos com barras de erro e dados brutos.
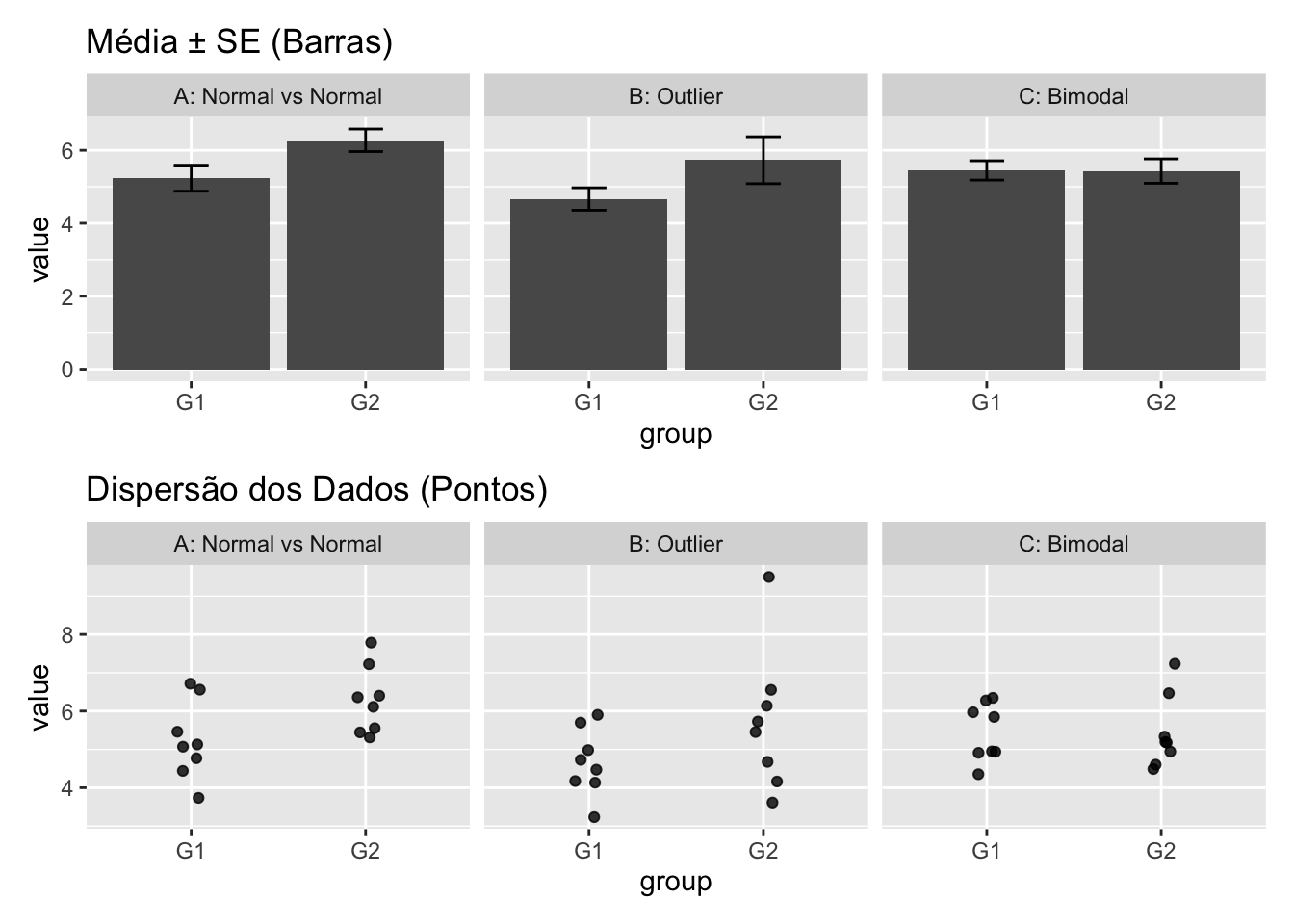
Figura 20.3: Exemplos de gráficos com barras de erro e dados brutos em diferentes cenários.
Os pacotes ggplot2177, plotly228 e corrplot229 fornecem diversas funções para construção de gráficos tais como ggplot, plot_ly e corrplot respectivamente.
20.7.5 Quais são os principais obstáculos para bons gráficos?
- Dificuldade técnica, negligência no ensino tradicional e o foco em “beleza” sem clareza podem levar a gráficos ruins, mesmo quando bem intencionados.227
20.8 Tipos de gráficos
20.8.1 Quais são os tipos de gráficos para variáveis categóricas?
- Gráfico de barras: Mais usado para comparar frequências absolutas ou relativas entre categorias.REF?
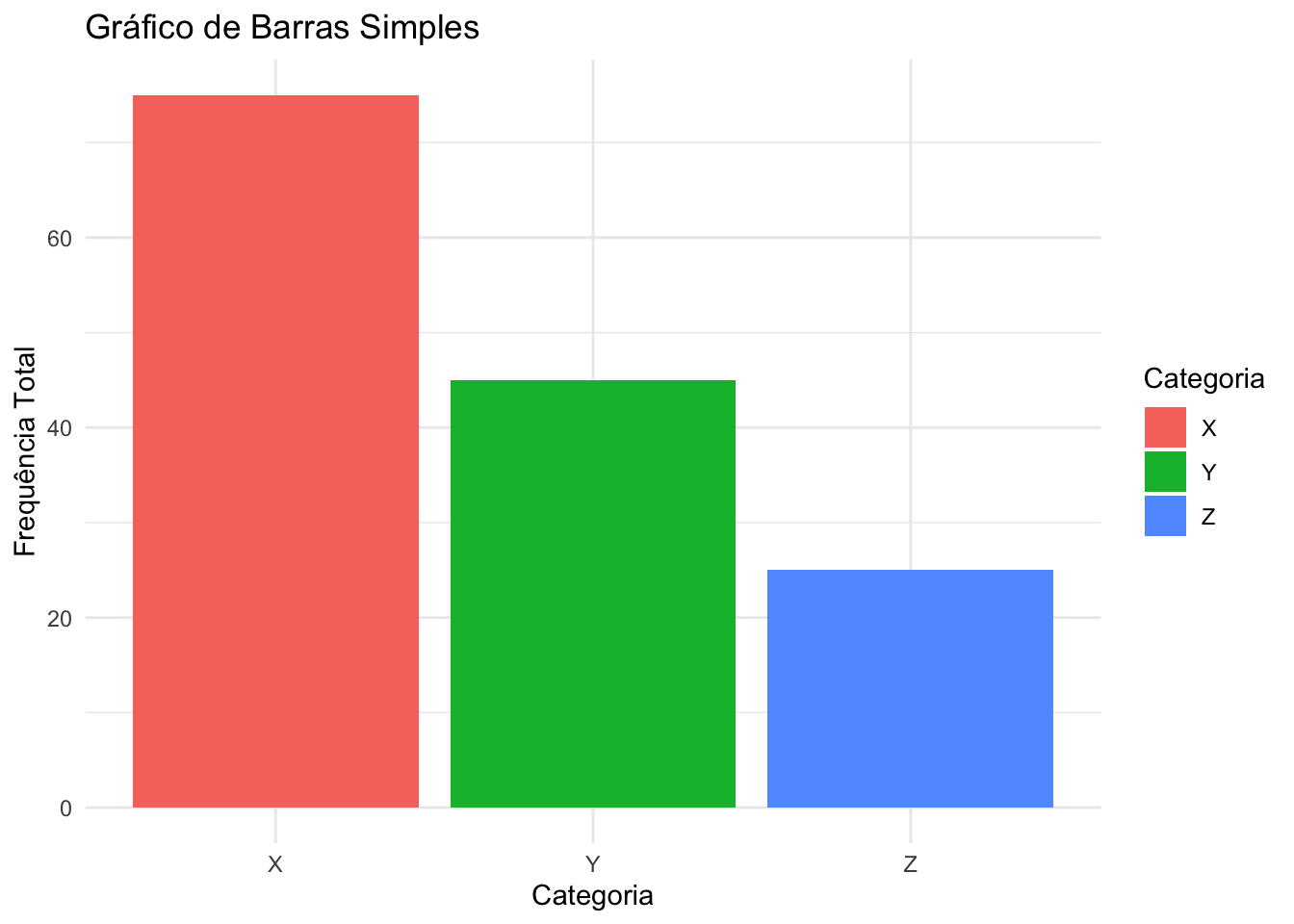
Figura 20.4: Gráfico de barras simples representando frequências por categoria.
- Gráfico de barras empilhadas: Útil para comparar proporções entre grupos em mais de uma variável categórica.REF?
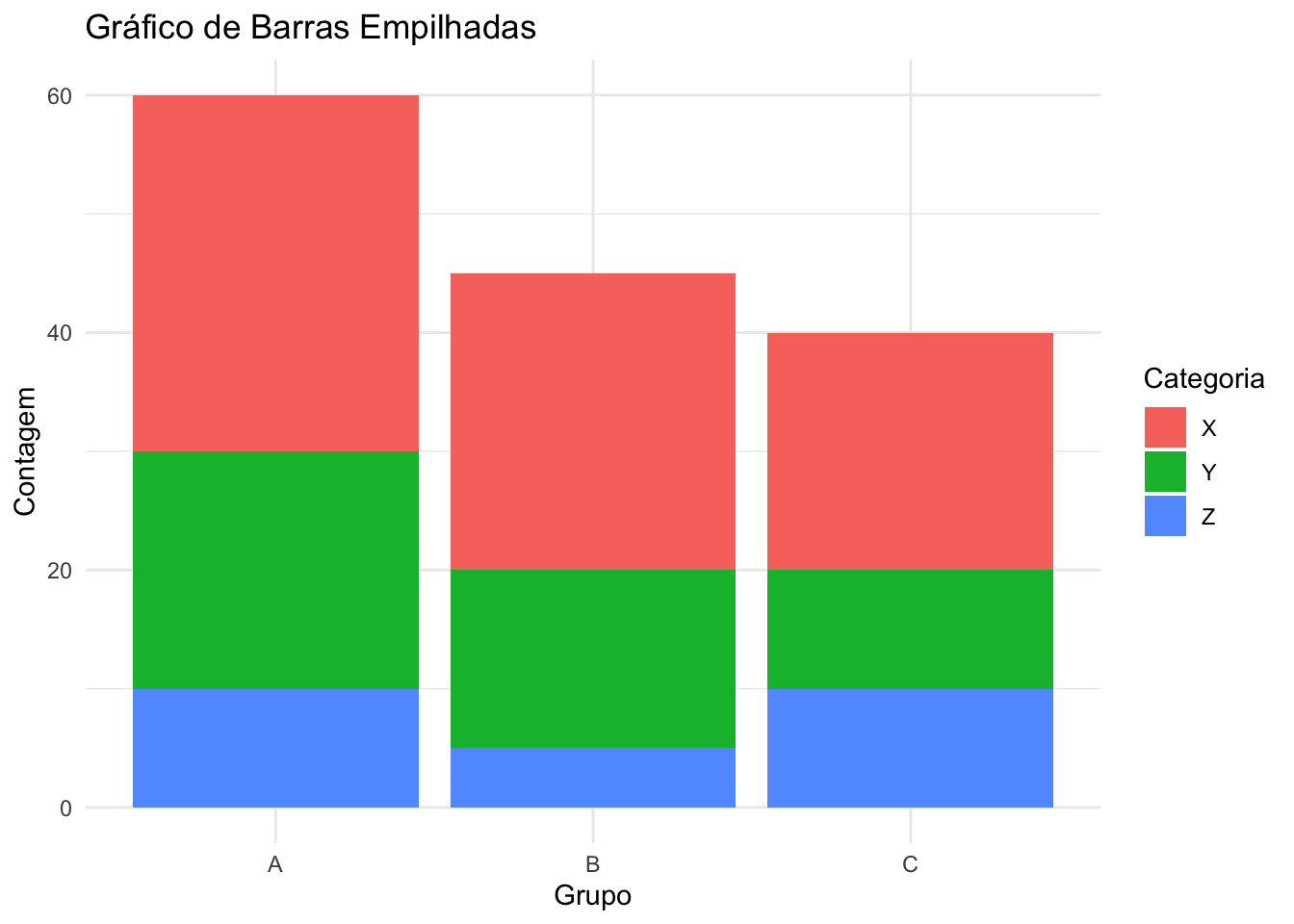
Figura 20.5: Gráfico de barras empilhadas representando frequências por categoria.
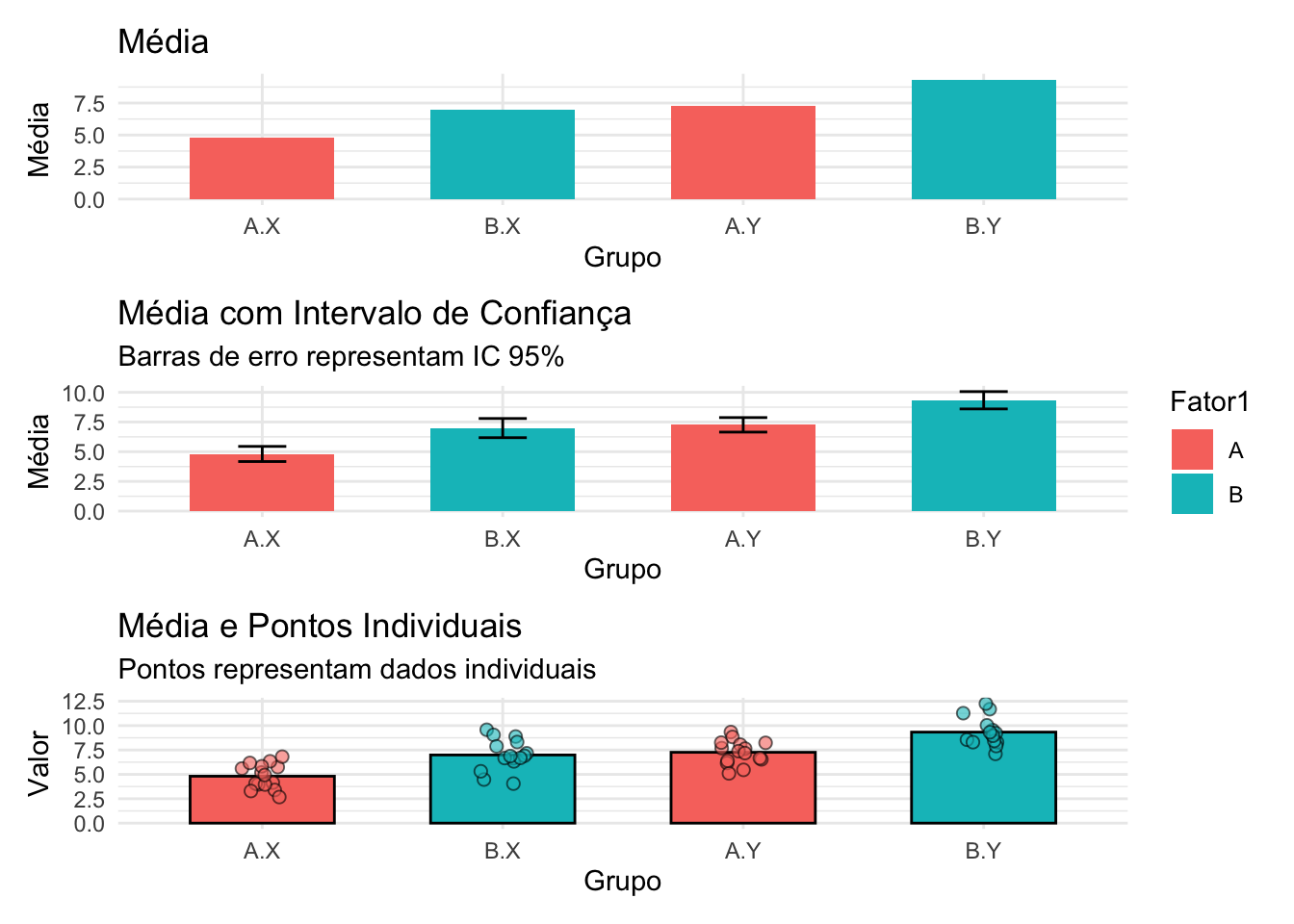
Figura 20.6: Gráficos de barras represetando médias, barras de erro e dados individuais.
20.8.2 Quais são os tipos de gráficos para variáveis numéricas?
- Histograma: Distribuição de frequência de uma variável contínua. Mostra a forma da distribuição (simétrica, assimétrica, bimodal).REF?
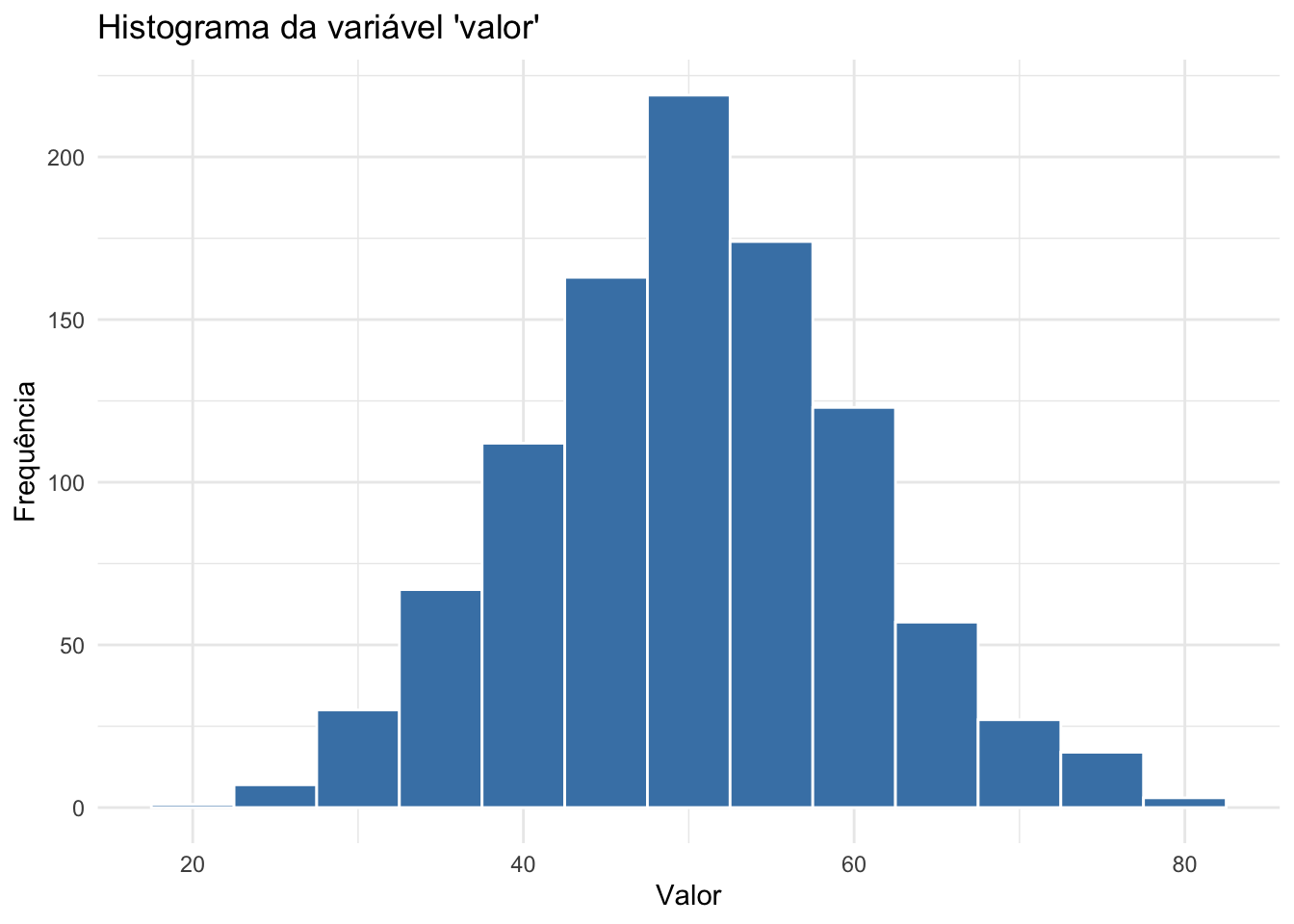
Figura 20.7: Histograma da variável ‘valor’.
- Gráfico de densidade: Similar ao histograma, mas mais suave. Útil para avaliar a distribuição.REF?
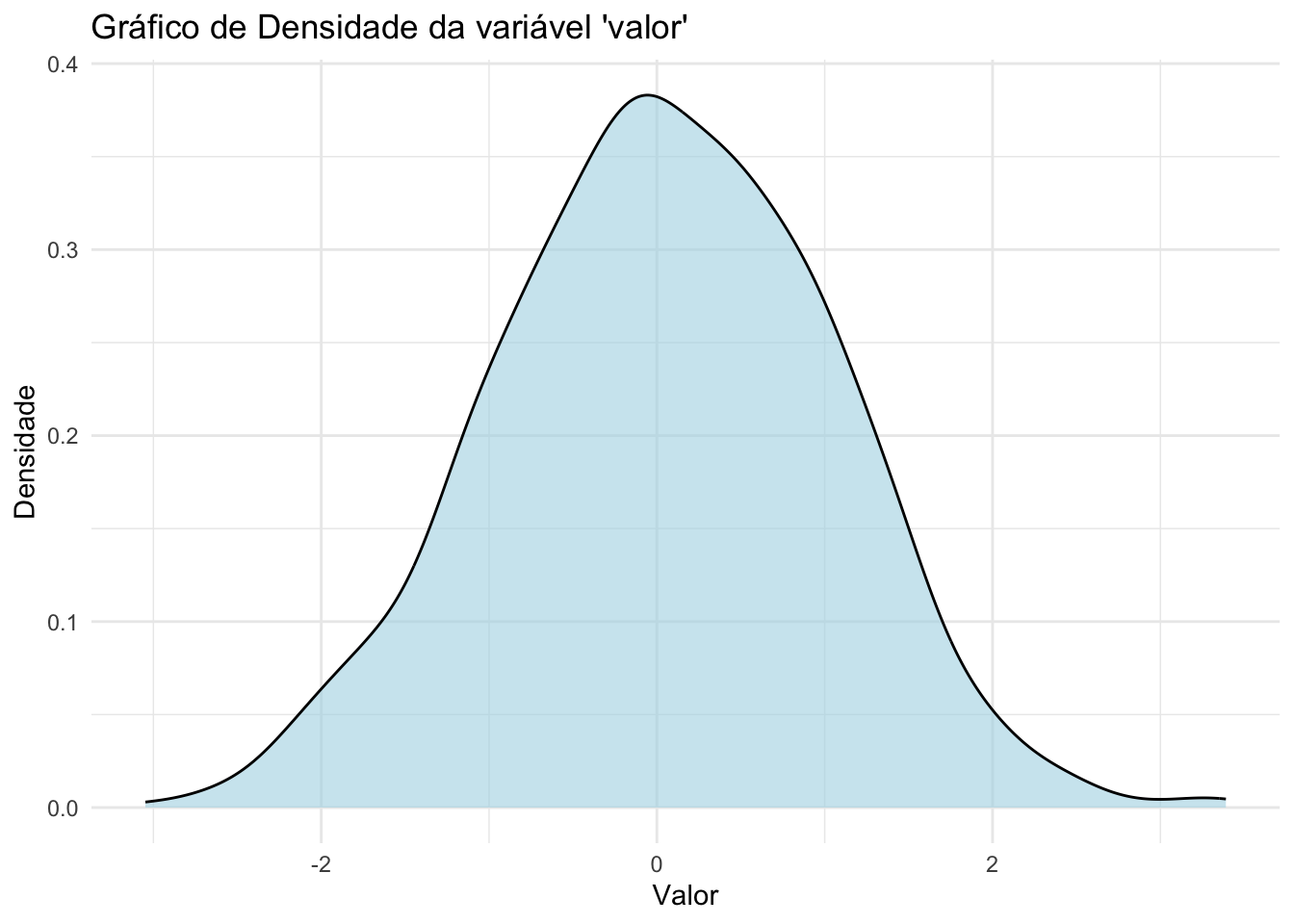
Figura 20.8: Gráfico de densidade da variável ‘valor’.
- Diagrama de caixa (boxplot): Resume mediana, quartis e valores extremos. Excelente para comparar grupos.REF?
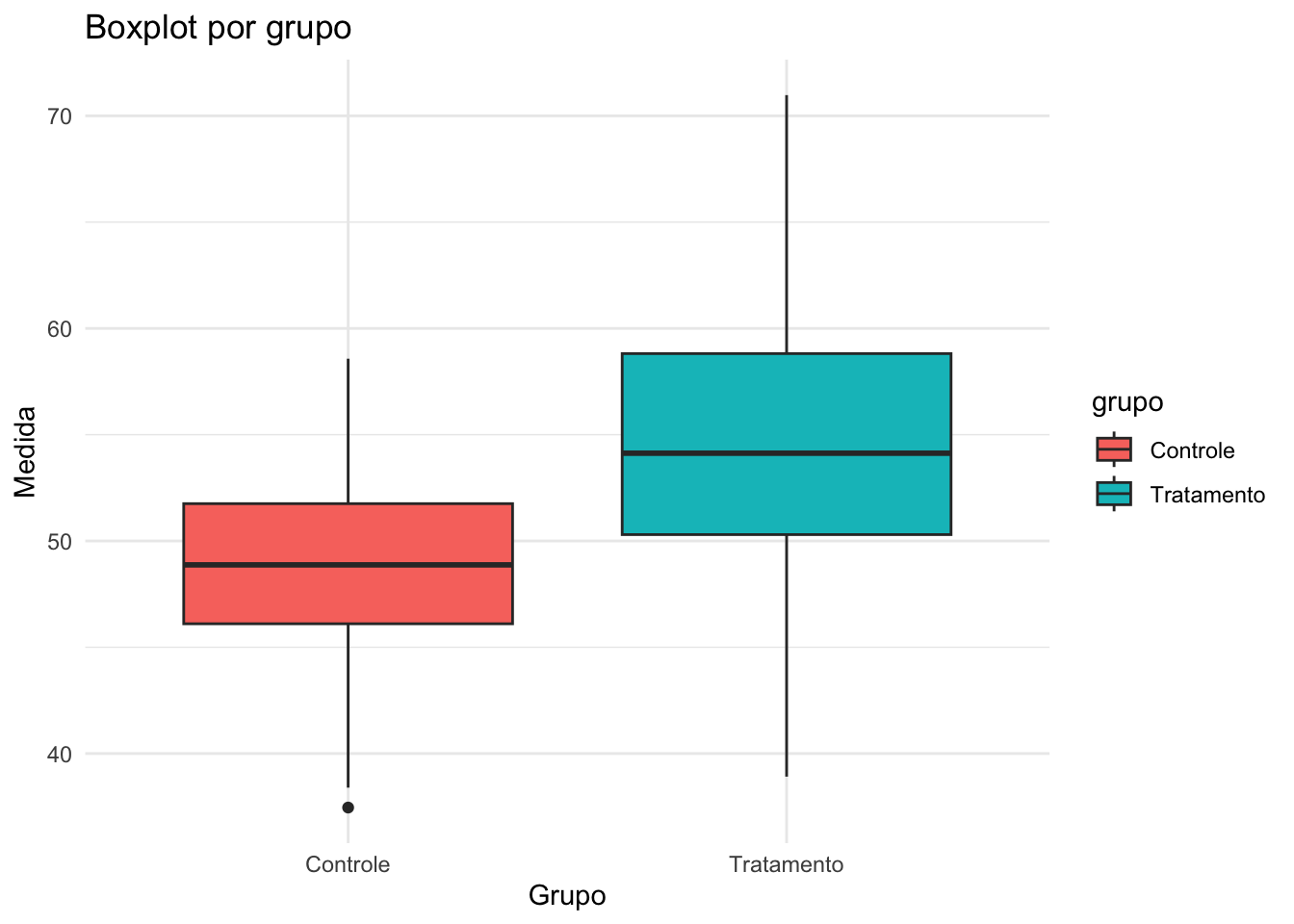
Figura 20.9: Boxplot por grupo.
- Gráfico de violino: Combina boxplot e densidade, mostrando a distribuição da variável. Útil para comparar grupos.REF?
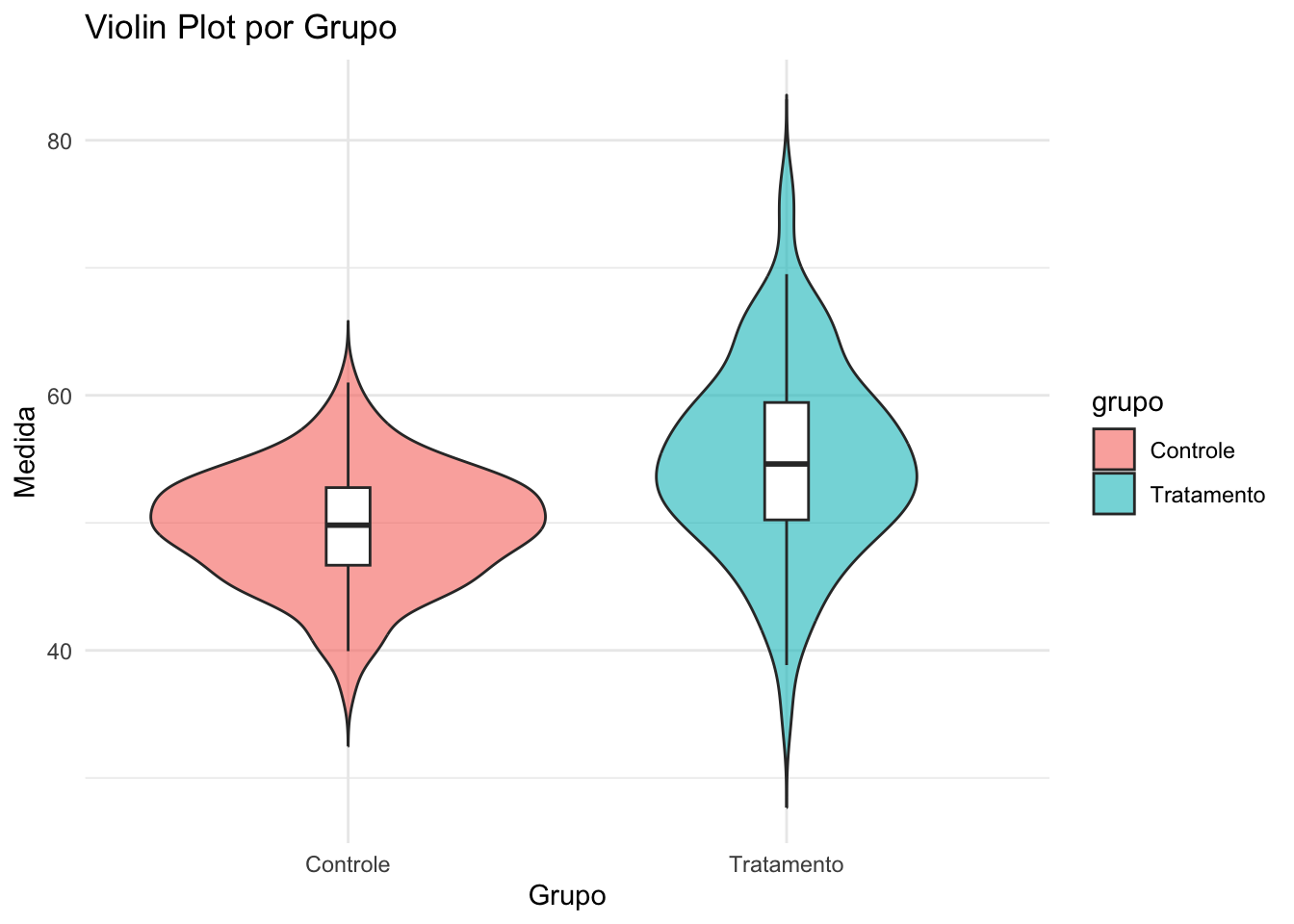
Figura 20.10: Violin plot por grupo.
- Gráfico de pontos (dot plot): Mostra cada valor individualmente, útil para pequenas amostras e para visualizar a distribuição.REF?
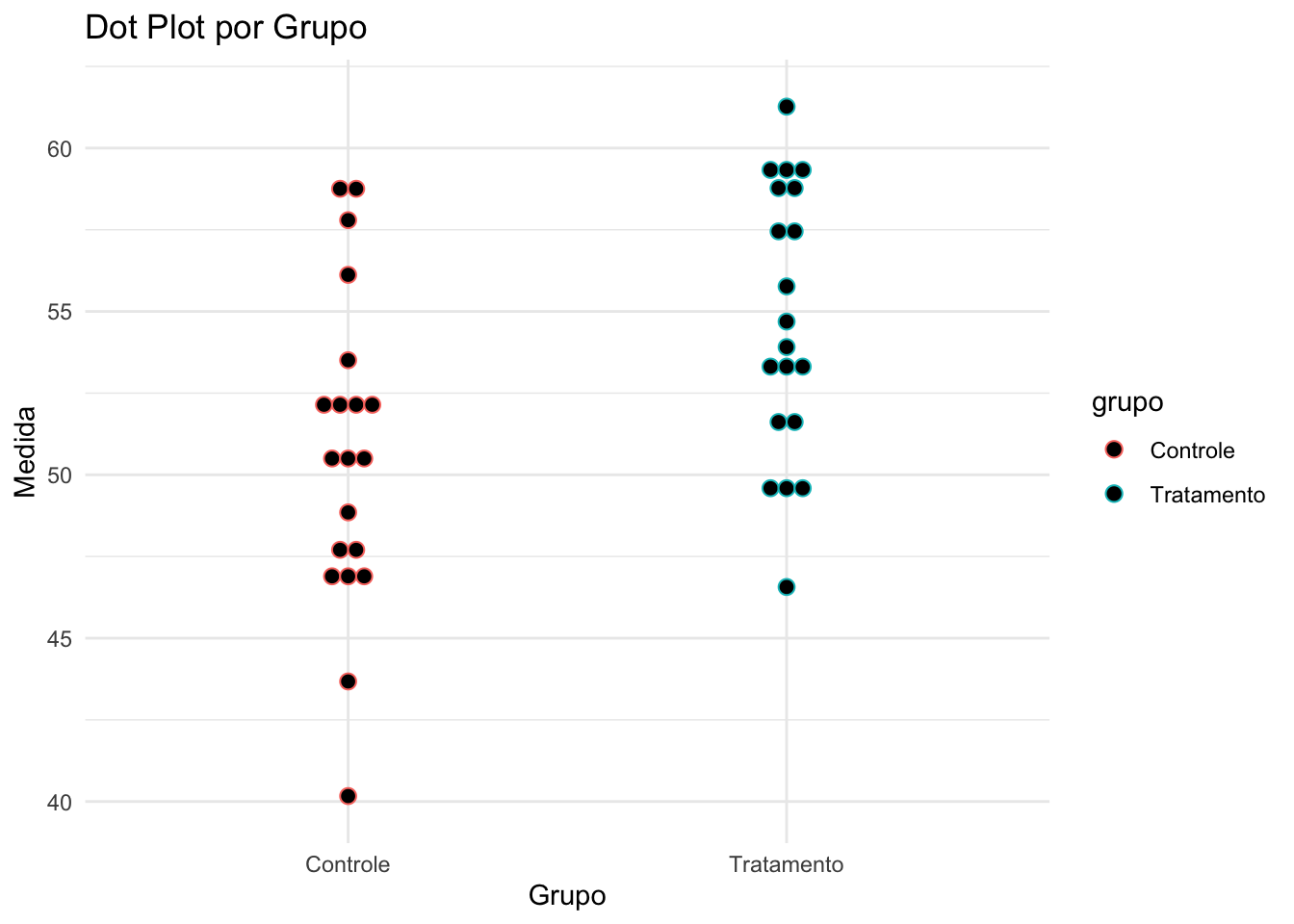
Figura 20.11: Gráfico de pontos da variável ‘valor’.
20.8.3 Quais são os tipos de gráficos para relações entre variáveis?
- Gráfico de dispersão (scatter plot): Mostra a relação entre duas variáveis quantitativas. Ideal para investigar correlações.REF?
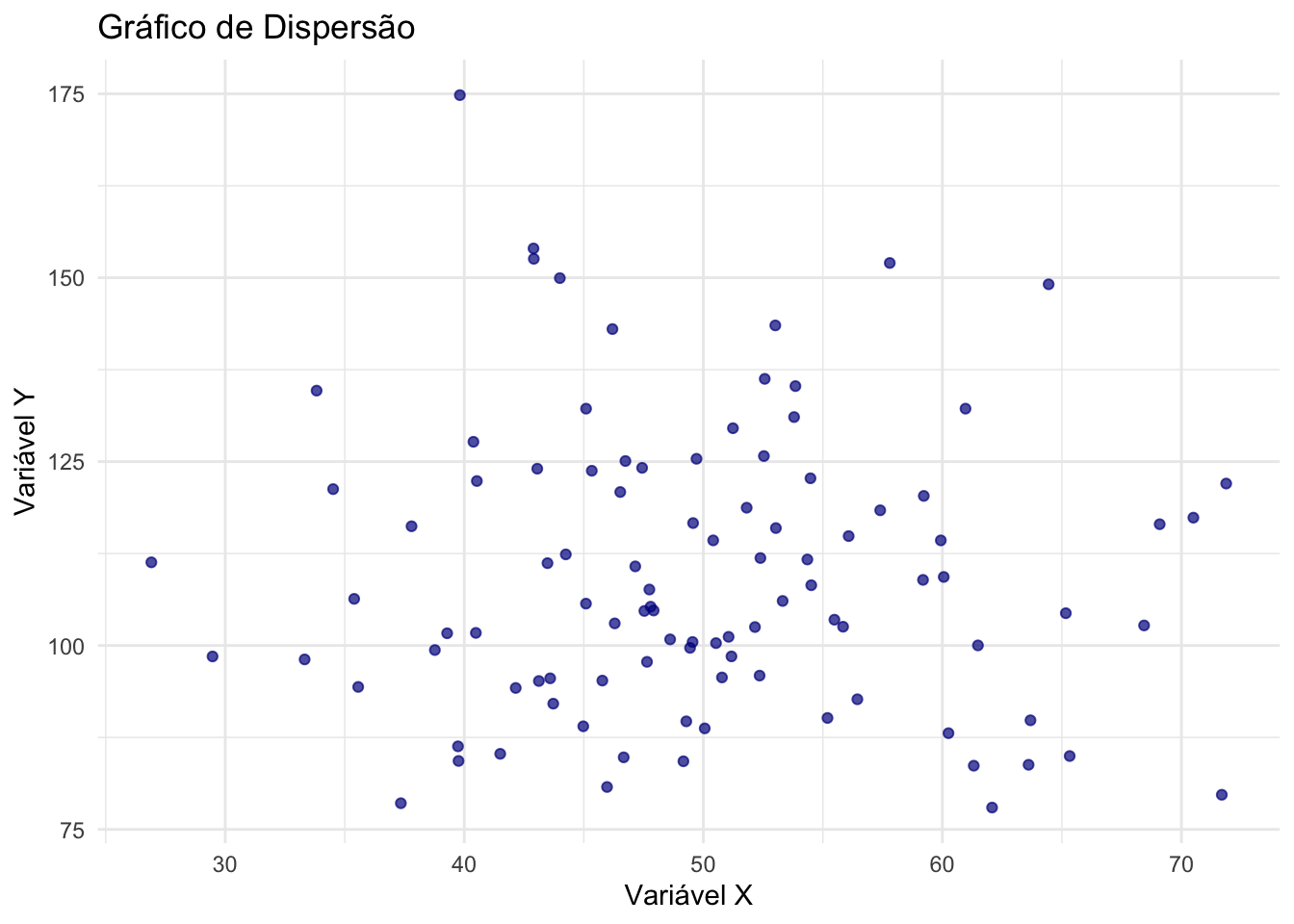
Figura 20.12: Gráfico de dispersão representando a relação entre duas variáveis.
- Gráfico de bolhas (bubble chart): Expande o gráfico de dispersão adicionando uma terceira variável (tamanho da bolha).REF?
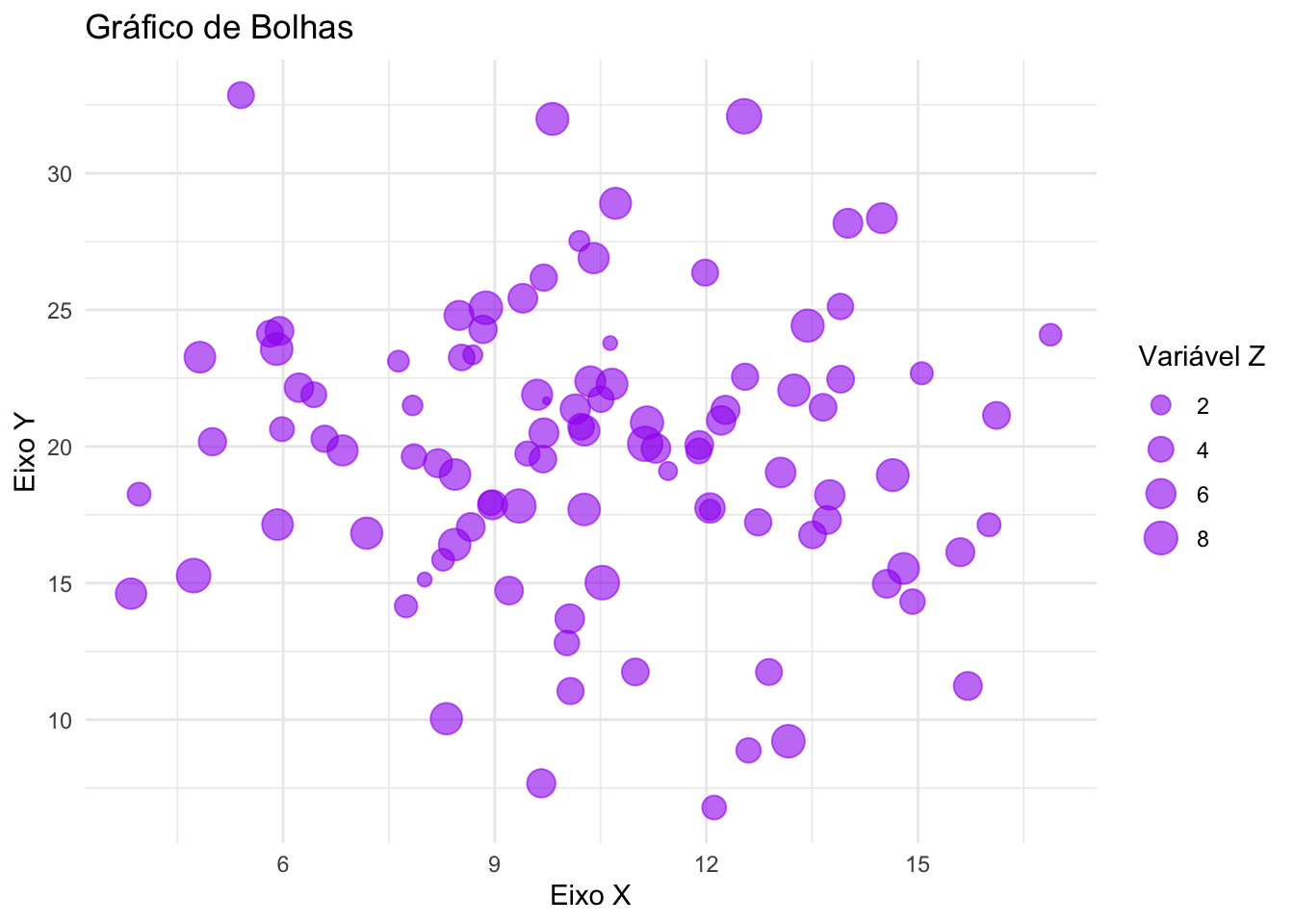
Figura 20.13: Gráfico de bolhas representando a relação entre três variáveis.
- Gr;afico Sankey: Visualiza fluxos entre categorias em diferentes etapas ou grupos. Útil para mostrar proporções e transições.REF?
Figura 20.14: Sankey plot representando fluxos entre categorias.
- Grágfico de parcats: Mostra relações entre múltiplas variáveis categóricas em paralelo. Útil para visualizar fluxos e proporções.REF?
Figura 20.15: Gráfico de categorias paralelas (parcats) representando transições entre categorias ao longo do tempo.
- Gráfico de parts: Mostra a composição percentual de uma variável categórica. Útil para visualizar proporções.REF?
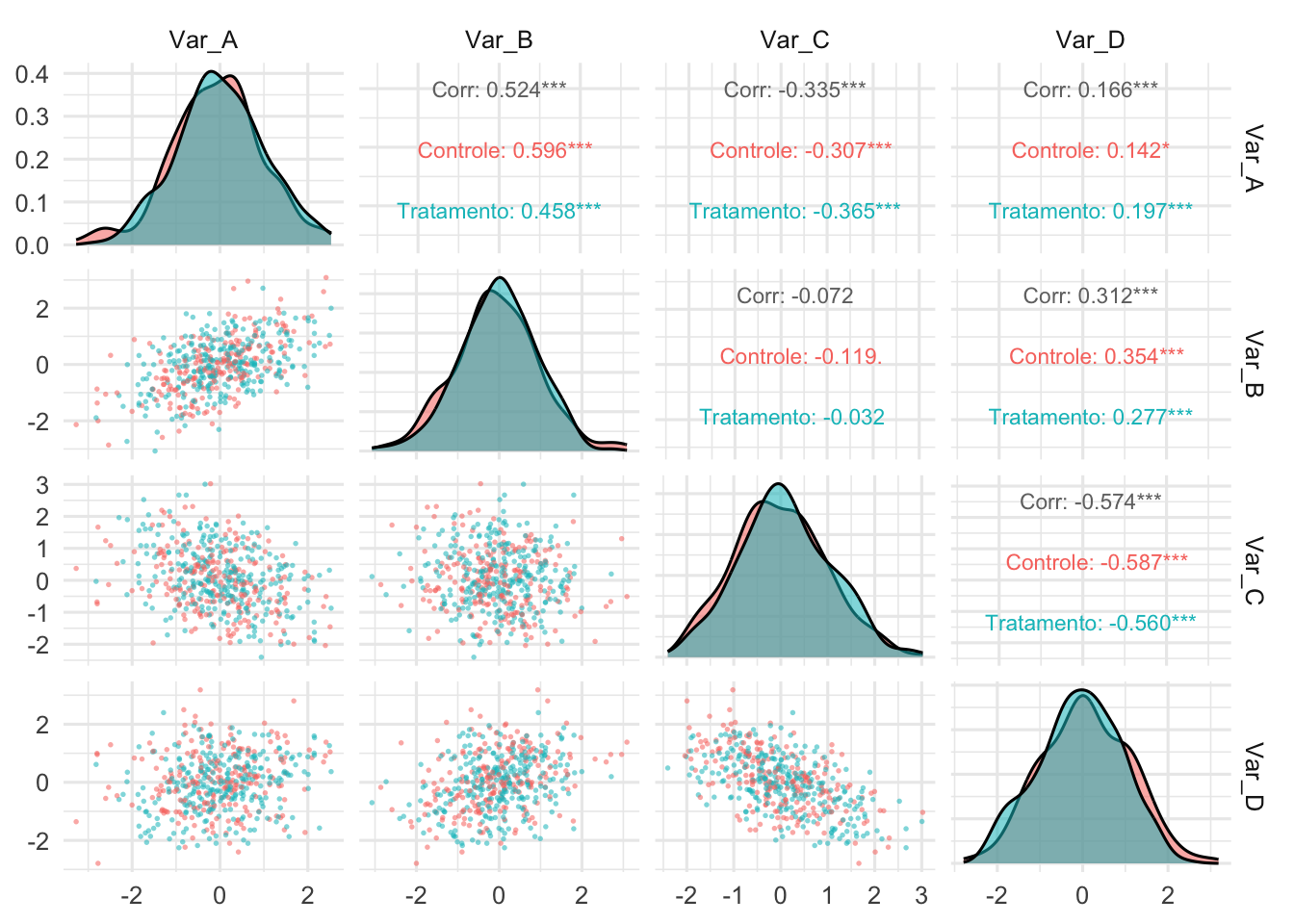
Figura 20.16: Gráfico de pares representando correlações entre múltiplas variáveis.
20.8.4 Quais são os tipos de gráficos para dados longitudinais?
- Gráfico de spaghetti: Mostra trajetórias individuais ao longo do tempo, útil para dados longitudinais.REF?
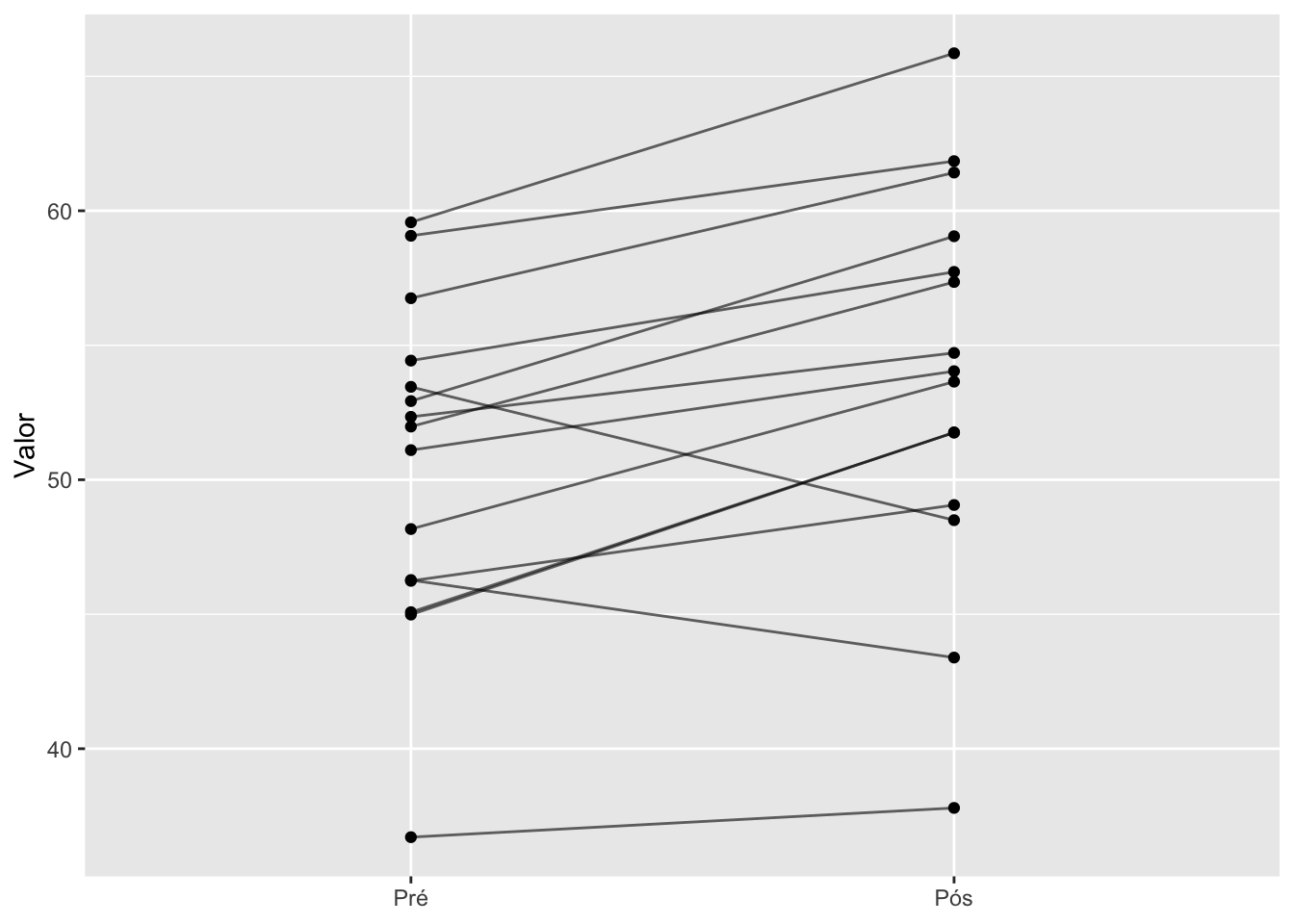
Figura 20.17: Gráfico spaghetti representando dados longitudinais.
20.8.5 Quais são os tipos de gráficos para séries temporais?
- Gráfico de linhas: Mostra a evolução de uma variável ao longo do tempo, com pontos conectados por linhas.REF?
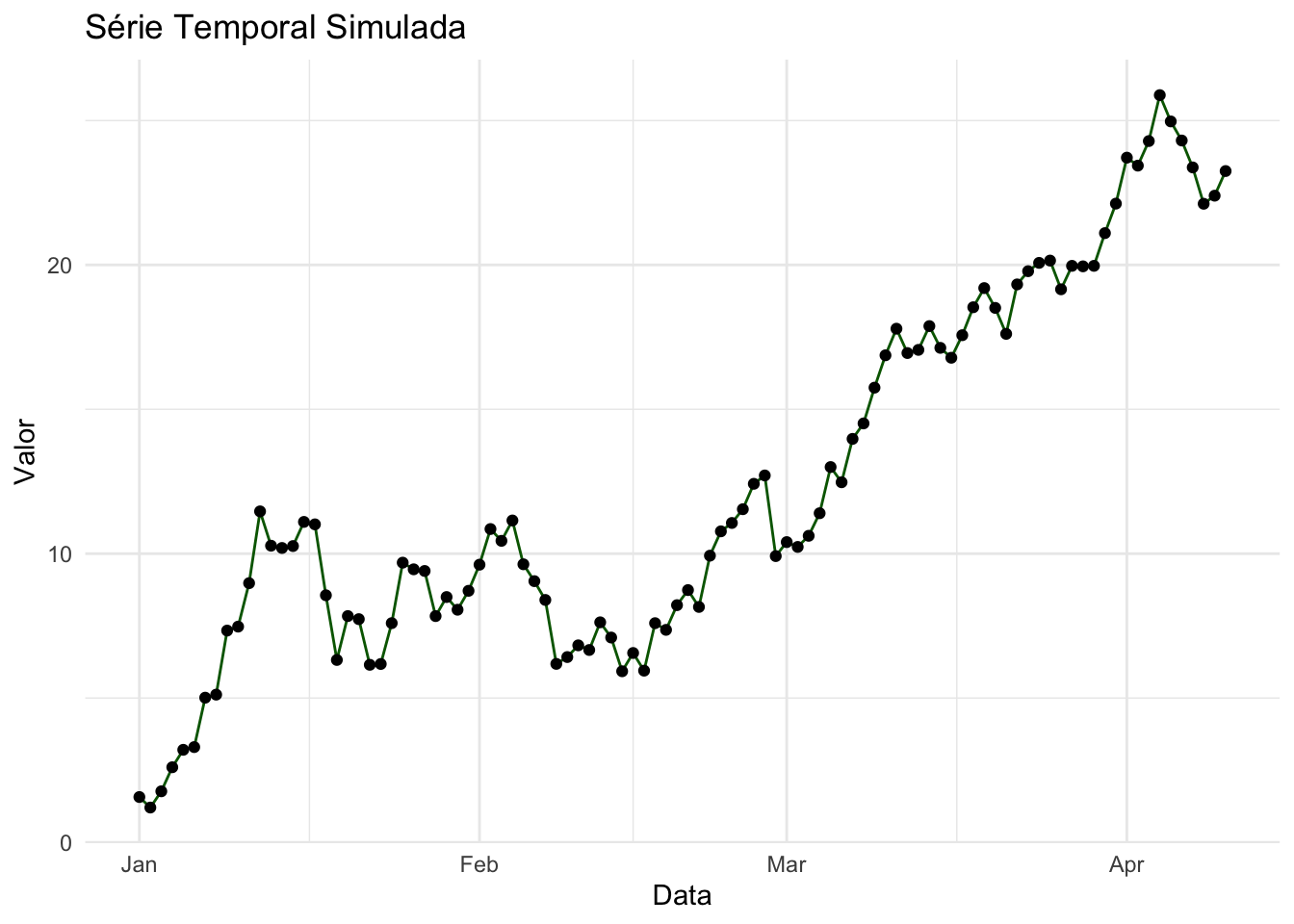
Figura 20.18: Gráfico de linha representando uma série temporal.
20.8.6 Quais são os tipos de gráficos para dados multivariados?
- Gráfico de dispersão: Representa a relação entre duas variáveis, com pontos e uma linha de tendência.REF?
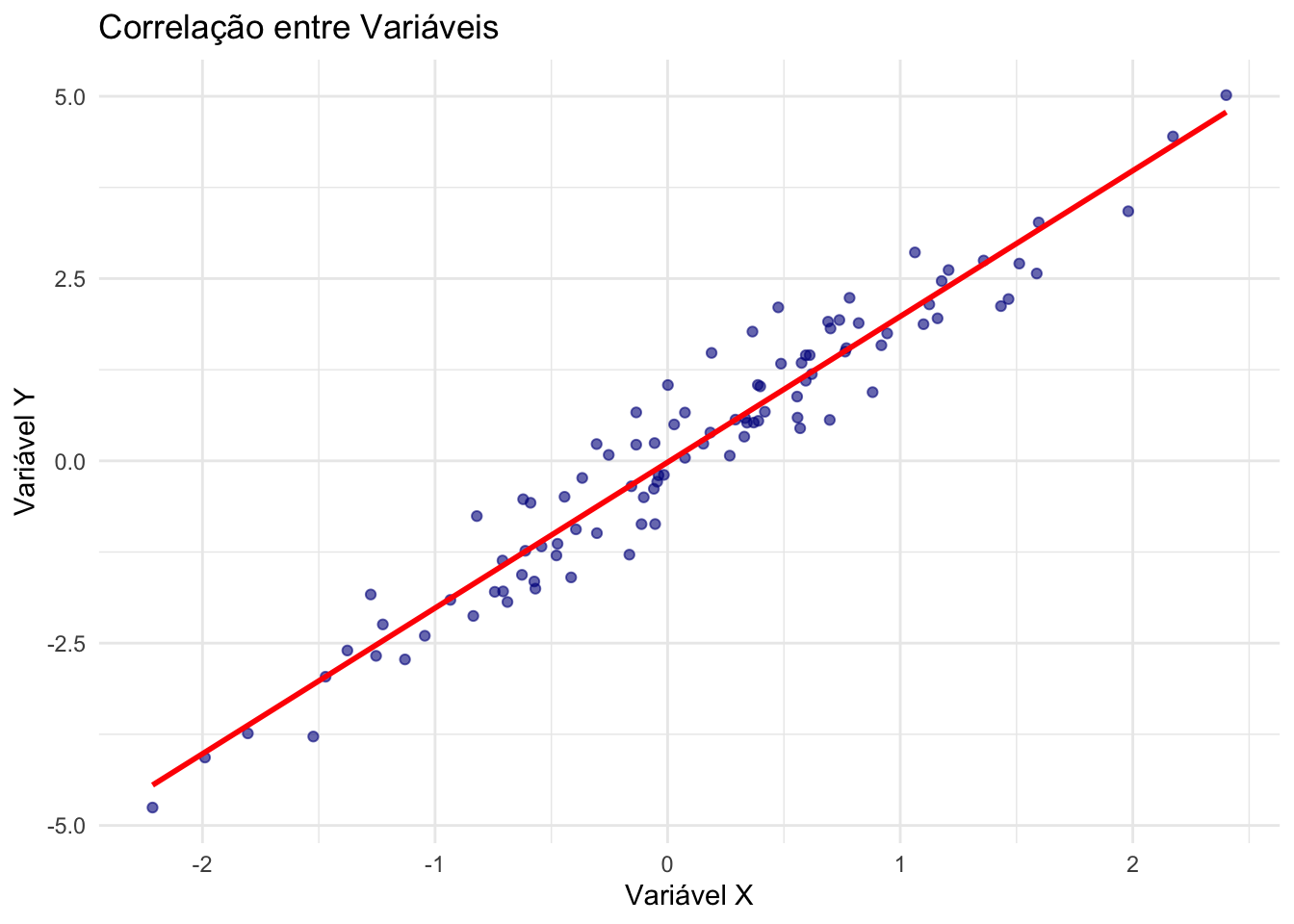
Figura 20.19: Gráfico de correlação entre duas variáveis com linha de tendência.
- Gráfico de matriz de dispersão: Mostra relações entre múltiplas variáveis quantitativas, útil para identificar padrões.REF?
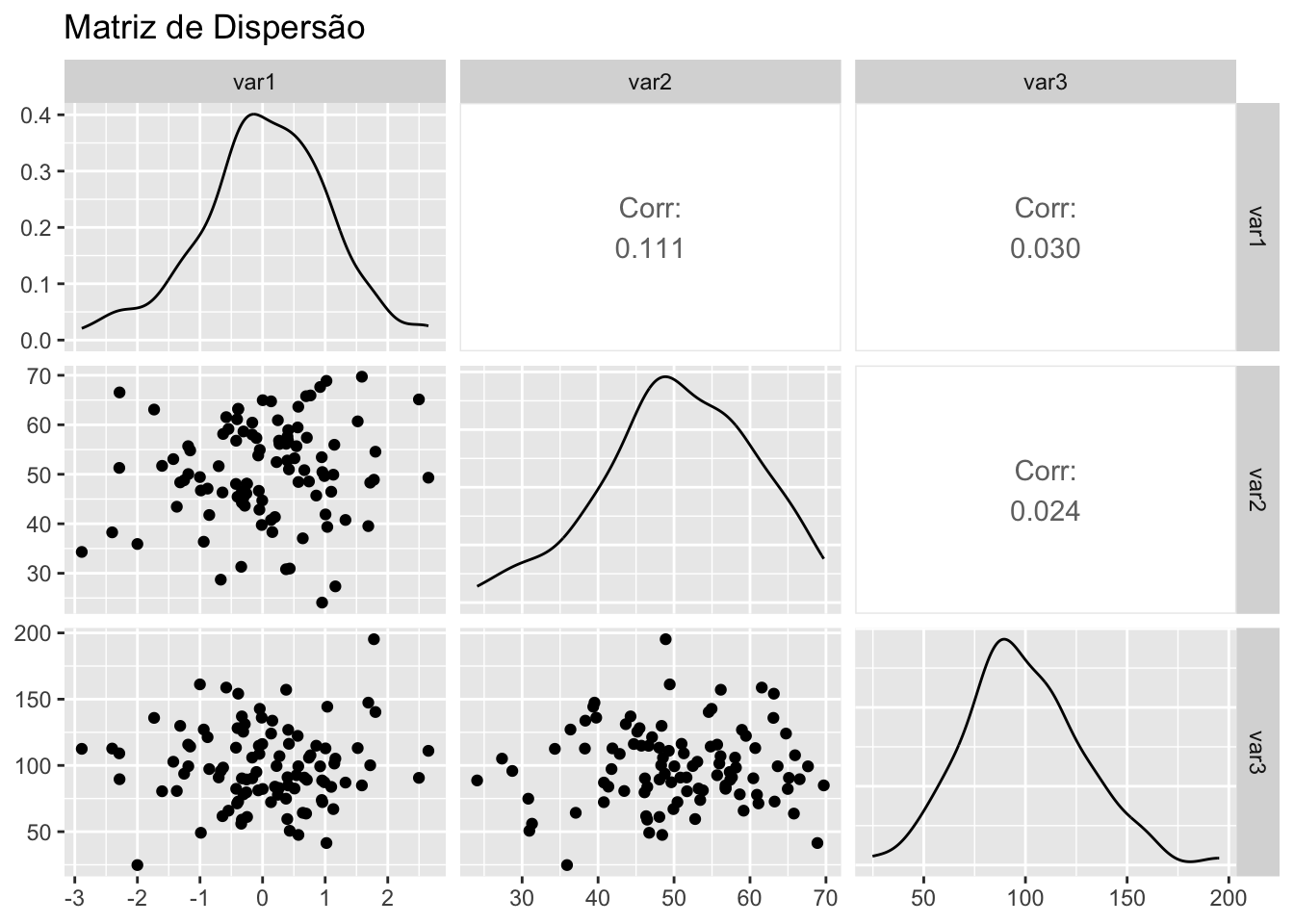
Figura 20.20: Matriz de dispersão representando relações entre múltiplas variáveis.
- Gráfico de calor (heatmap): Representa dados em uma matriz, com cores indicando intensidade ou frequência.REF?
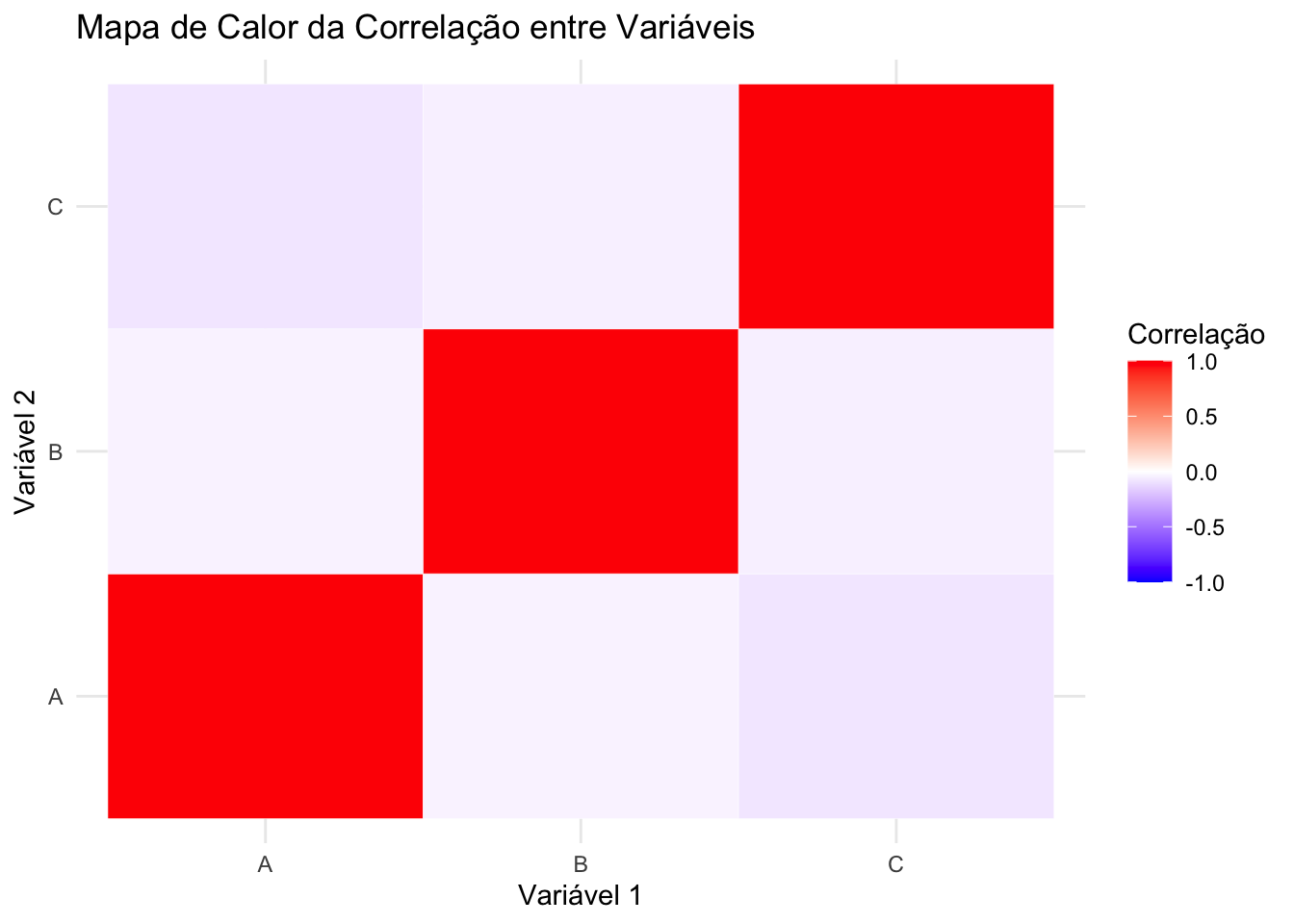
Figura 20.21: Mapa de calor da correlação entre variáveis.
- Gráfico de radar (ou gráfico de aranha): Representa várias variáveis em um único gráfico, útil para comparar perfis.REF?
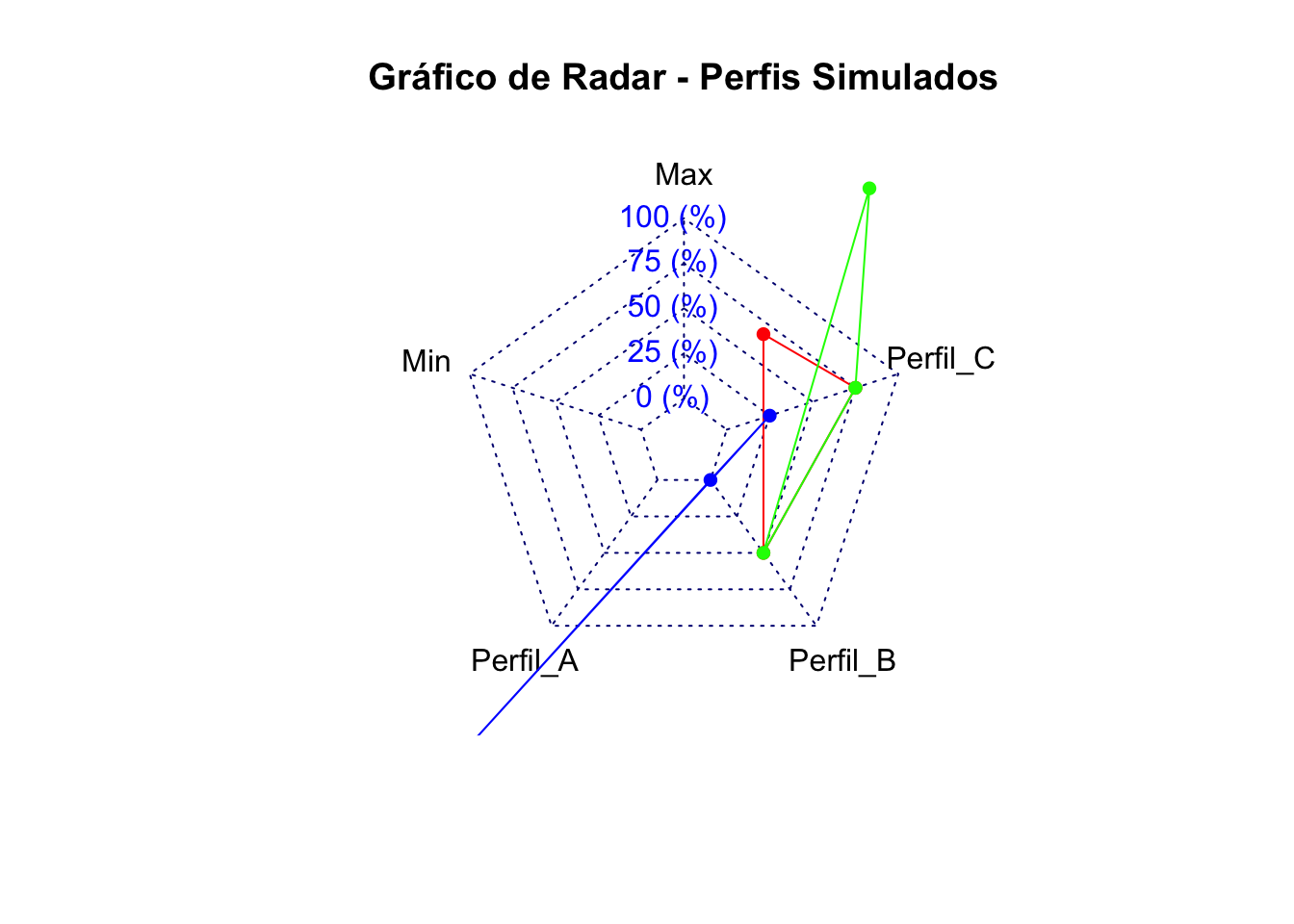
Figura 20.22: Gráfico radar representando múltiplas variáveis.
20.8.7 Quais são as boas práticas na elaboração de gráficos?
O tamanho da amostra total e subgrupos, se houver, deve estar descrito na figura ou na sua legenda.187
Para análise inferencial de figuras, as barras de erro representadas por erro-padrão ou intervalo de confiança no nível de significância \(\alpha\) pré-estabelecido são preferíveis à amplitude ou desvio-padrão.186,187
Evite gráficos de barra e mostre a distribuição dos dados sempre que possível.212
Exiba os pontos de dados em boxplots.212
Use jitter simétrico em gráficos de pontos para permitir a visualização de todos os dados.212
Prefira palhetas de cor adaptadas para daltônicos.212
Uma boa legenda torna a figura autossuficiente: descreva amostra (n), geometrias, métricas de incerteza, escalas/unidades e mensagem principal. Se houver modelo, indique fórmula/ajustes em nota.225
Evite gráficos de barras com médias para variáveis contínuas; prefira pontos/box/violino e, em amostras pequenas, exiba todos os dados.212
Antes de finalizar um gráfico, faça as seguintes perguntas: (1) Mensagem está explícita? (2) Geometria adequada e dados visíveis? (3) Incerteza correta e rotulada? (4) Cores informativas e acessíveis? (5) Escalas comparáveis (se facetou)? (6) Legenda/caption autossuficiente? (7) Diferença clara entre dados e modelos? (8) Arquivo exportado na resolução/tamanho exigidos?225
O pacote ggsci230 fornece palhetas de cores tais como pal_lancet, pal_nejm e pal_npg inspiradas em publicações científicas para uso em gráficos.
O pacote grDevices176 fornece a função dev.new para controlar diversos aspectos do gráfico, tais como tamanho e resolução.
20.9 Gráficos dinâmicos
20.9.1 O que são visualizações dinâmicas?
- Visualizações dinâmicas combinam interatividade (exploração ativa pelo leitor) e animação (mudanças ao longo do tempo/iterações) para empacotar informação rica em exibições simples, tornando comunicação e exploração mais transparentes.232
20.9.2 Quando preferir interatividade?
- Durante exploração de dados em equipe: destacar pontos/linhas por participante, filtrar subconjuntos e inspecionar impactos de escolhas analíticas (p.ex., outliers) sem gerar múltiplas figuras novas.232
Figura 20.23: Exemplo de gráfico interativo com Plotly.
20.9.3 Quando preferir animação?
- Em apresentações e para ilustrar variação ao longo de tempo/condição/algoritmo, evitando painéis 3D ou facets excessivos. A animação guia a atenção e revela mudanças de forma passiva e fluida.232
O pacote gganimate233 fornece a função transition_states para criar gráficos animados a partir de gráficos estáticos do ggplot2177.
Ferreira, Arthur de Sá. Ciência com R: Perguntas e respostas para pesquisadores e analistas de dados. Rio de Janeiro: 1a edição,