Capítulo 28 Tamanho do efeito e P-valor
28.1 Tamanho do efeito
28.1.1 O que é o tamanho do efeito?
- Tamanho do efeito quantifica a magnitude de um efeito real da análise, expressando uma importância descritiva dos resultados.281
28.2 Tipos de tamanho do efeito
Diferenças padronizadas entre grupos:271,281
Cohen’s \(d\)
Glass’s \(\Delta\)
Razão de chances (\(RC\) ou \(OR\))
Risco relativo ou razão de risco (\(RR\))
O pacote epitools282 fornece a função oddsratio.wald para calcular a razão de chances.
O pacote epitools282 fornece a função riskratio.wald para calcular a razão de risco.
-
Coeficiente de correlação de Pearson (\(r\)), ponto-bisserial (\(r_{s}\)), Spearman (\(\rho\)), Kendall (\(\tau\)), Cramér (\(V\)) e \(\phi\).
Coeficiente de determinação (\(R^2\))
28.2.1 Como interpretar um tamanho do efeito?
- Tamanhos de efeito podem ser comparadores entre diferentes estudos.271
O pacote effectsize283 fornece a função rules para criar regras de interpretação de tamanhos de efeito.
O pacote effectsize283 fornece a função interpret para interpretar os tamanhos de efeito com base em uma lista de regras pré-definidas.
O pacote pwr284 fornece a função cohen.ES para obter os tamanhos de efeito “pequeno”, “médio” e “grande” para diversos testes de hipóteses.
28.2.2 O que é a diferença de média bruta?
A diferença de média bruta representa a diferença absoluta entre as médias de dois grupos, expressa na unidade original da variável.REF?
Trata-se de uma medida não padronizada, sendo particularmente útil quando a escala possui interpretação clínica ou substantiva direta (por exemplo, mmHg, pontos de escore).REF?
Por depender da unidade de medida, não permite comparações diretas entre estudos com métricas diferentes.REF?
28.2.3 Correlações podem ser consideradas tamanhos de efeito?
Sim. Coeficientes de correlação podem ser interpretados diretamente como tamanhos de efeito, pois expressam a força e a direção da associação entre variáveis.REF?
O coeficiente de Spearman (\(\rho\)) mede associações monotônicas e é robusto a violações de normalidade.REF?
Kendall (\(\tau\)) é especialmente indicado para amostras pequenas ou dados com empates.REF?
Esses coeficientes são frequentemente utilizados como tamanhos de efeito em testes não paramétricos.REF?
28.2.4 O que é o \(q\) de Cohen?
O tamanho de efeito \(q\) quantifica a diferença entre dois coeficientes de correlação, após transformação de Fisher (\(z\)).REF?
É utilizado principalmente para comparar associações observadas em grupos independentes.REF?
Cohen propôs valores de referência para interpretação (pequeno, médio e grande), reforçando seu caráter descritivo.REF?
28.2.5 O que o \(g\) no teste do sinal?
O coeficiente \(g\) é utilizado como tamanho de efeito no teste do sinal.REF?
Representa a diferença padronizada entre a proporção de observações positivas e negativas.REF?
Aplica-se a delineamentos pareados em que apenas a direção do efeito é considerada.REF?
É uma medida robusta, porém menos informativa do que medidas baseadas em magnitude contínua.REF?
28.2.6 O que é o \(h\) de Cohen?
O tamanho de efeito \(h\) mede a diferença entre duas proporções, após transformação angular para estabilizar a variância.REF?
É indicado para comparações entre desfechos binários.REF?
Por ser padronizado, permite comparações entre estudos com diferentes proporções absolutas.REF?
28.2.7 O que representa o tamanho de efeito \(w\)?
O coeficiente \(w\) é utilizado como tamanho de efeito em testes do qui-quadrado, tanto de aderência quanto de independência.REF?
Quantifica o grau global de discrepância entre frequências observadas e esperadas.REF?
Sua interpretação depende do número de categorias e do tamanho da amostra, devendo ser feita com cautela.REF?
28.2.8 O que é o tamanho de efeito \(f\) em ANOVA?
O coeficiente \(f\) é utilizado como tamanho de efeito em análises de variância (ANOVA).REF?
Está relacionado à proporção da variância explicada pelo fator em relação à variância residual.REF?
É amplamente empregado em cálculos de poder estatístico e no planejamento amostral.REF?
28.2.9 O que é o tamanho de efeito \(f^2\) em regressão?
O coeficiente \(f^2\) mede o impacto incremental de um conjunto de preditores em modelos de regressão.REF?
É definido como a razão entre a variância explicada adicional e a variância não explicada.REF?
É particularmente útil para avaliar contribuições locais em modelos hierárquicos ou multivariados.REF?
28.2.10 O que é a estatística \(\Lambda\) de Wilks na MANOVA?
O Lambda de Wilks (\(\Lambda\)) é utilizado como estatística global em análises multivariadas de variância (MANOVA).REF?
Representa a proporção da variância multivariada não explicada pelo modelo.REF?
Embora menos intuitivo como medida de magnitude, é amplamente utilizado e pode ser convertido em outras estatísticas.REF?
28.2.11 Como escolher o tamanho de efeito adequado?
Não existe um tamanho de efeito universalmente superior; a escolha depende da pergunta científica, do delineamento, do tipo de variável e do modelo estatístico.REF?
A boa prática estatística recomenda reportar estimativa pontual, intervalo de confiança e tamanho de efeito, evitando decisões baseadas exclusivamente em significância estatística.REF?
Sempre que possível, a interpretação deve considerar relevância prática, contexto científico e incerteza associada.REF?
28.5 P-valor
28.5.1 O que é significância estatística?
- A expressão “significância estatística”287 ou “evidência estatística de significância” sugere apenas que um experimento merece ser repetido, uma vez que um baixo P-valor (calculado a partir dos dados, modelos e demais suposições do estudo) sugere ser improvável que os dados coletados sejam coletados no contexto de que a hipótese nula (\(H_{0}\)) assumida é verdadeira.288
28.5.2 Como justificar o nível de significância estatística de um teste?
- .REF?
O pacote Superpower289 fornece a função optimal_alpha para calcular e justificar o nível de significância \(\alpha\) por balanço dos erros tipo I e II.
O pacote Superpower289 fornece a função ANOVA_compromise para calcular e justificar o nível de significância \(\alpha\) por balanço dos erros tipo I e II em análise de variância (ANOVA).
28.5.3 O que é o P-valor?
P-valor é a probabilidade, assumindo-se um dado modelo estatístico, de que um efeito calculado a partir dos dados seria igual ou mais extremo do que o seu valor observado.290
P-valor é uma variável aleatória que possui distribuição uniforme quando a hipótese nula (\(H_{0}\)) é verdadeira.291
28.5.4 Como interpretar o P-valor?
P-valores abaixo de um nível de significância estatística pré-especificado representam que um experimento merece ser repetido, com a rejeição da hipótese nula (\(H_{0}\)) justificada apenas quando experimentos adicionais frequentemente reportem igualmente resultados positivos (rejeição da hipótese nula (\(H_{0}\)).273
P-valor resulta da coleta e análise de dados, e assim quantifica a plausibilidade dos dados observados sob a hipótese nula (\(H_{0}\)).292
P-valores podem indicar quantitativamente a incompatibilidade entre os dados obtidos e o modelo estatístico especificado a priori (geralmente constituído pela hipótese nula (\(H_{0}\)).290
P-valores menores/maiores do que o nível de significância estatístico pré-estabelecido não devem ser utilizados como única fonte de informação para tomada de decisão em ciência.290
28.5.5 O que o P-valor não é?
P-valor não representa a probabilidade de que a hipótese nula (\(H_{0}\)) seja verdadeira, nem a probabilidade de que os dados tenham sido produzidos pelo acaso.290
P-valor não mede o tamanho do efeito ou a relevância da sua observação.290
P-valor sozinho não provê informação suficiente sobre a evidência sobre um modelo teórico. A sua interpretação correta requer uma descrição ampla sobre o delineamento, métodos e análises estatísticas aplicados no estudo.290
Evidência estatística de significância não provê informação sobre a magnitude do efeito observado e não necessariamente implica que o efeito é robusto.197,291
28.5.6 Qual a origem do ‘P<0,05’?
A origem do P<0,05 remonta aos trabalhos de R. A. Fisher nas décadas de 1920 e 1930. Fisher introduziu o conceito de P-valor dentro de uma abordagem frequentista de inferência estatística.273
O P<0,05 foi sugerido por Ronald A. Fisher como um limiar prático para indicar que um resultado era “estatisticamente significativo”.273
Para Ronald A. Fisher, a significância estatística não era prova definitiva, mas um sinal de que o resultado merecia investigação adicional. A rejeição da hipótese nula só deveria ocorrer após repetidas observações significativas, e não com base em um único teste.273
Figura 28.1: Visualização espacial de p < 0,05 (5 quadrados aleatórios em 100).
28.6 P-valor de 2ª geração
28.6.1 O que é o P-valor de 2ª geração?
O P-valor de 2ª geração (SGPV) resume a fração das hipóteses apoiadas pelos dados que também pertencem à hipótese nula intervalar (intervalo de equivalência previamente especificado). Quantifica quanto do intervalo de estimativa (p.ex., IC95%) recai dentro da zona de indiferença científica/clinicamente irrelevante.293
Essa abordagem exige declarar a hipótese nula como intervalo (e não um ponto), incorporando o que é considerado “efeito sem relevância prática” segundo o contexto científico (precisão de medida, relevância clínica etc.).293
28.6.2 Como definir a hipótese nula intervalar e \(\delta\)?
Especifique \(H_0\) como um intervalo de equivalência \([H_0^{-}, H_0^{+}]\) que contém efeitos considerados praticamente nulos. Defina \(\delta\) como a meia-largura do intervalo de equivalência (\(\delta = (H_0^{+} - H_0^{-})/2\)).293
A escolha deve ser a priori e justificada por critérios científicos (p.ex., MCID, precisão de medida).293
28.6.3 Como calcular o SGPV?
- Seja \(I=[a,b]\) o intervalo apoiado pelos dados (p.ex., IC 95%) e \(H_0\) o intervalo nulo. O SGPV é (28.1), onde \(|I|\) é a largura do intervalo de estimativa, \(|H_0|\) é a largura do intervalo nulo e \(|I \cap H_0|\) é a largura da sobreposição entre os dois intervalos. O SGPV é restrito ao intervalo \([0,1]\).293
\[\begin{equation} \tag{28.1} p_{\delta} = \frac{|\,I \cap H_0\,|}{|\,I\,|} \times \max\!\left\{ \frac{|\,I\,|}{2|\,H_0\,|}, \, 1 \right\} \end{equation}\]
Quando \(|I|<2|H_0|\), \(p_{\delta}\) é apenas a fração de sobreposição \(|I\cap H_0|/|I|\).293
Quando \(|I|>2|H_0|\), o SGPV reduz-se a \(\tfrac{1}{2}\times \dfrac{|,I\cap H_0,|}{|,H_0,|}\le \tfrac{1}{2}\), sinalizando inconclusão por imprecisão.293
| Cenário | \(a\) | \(b\) | \(H_0^{-}\) | \(H_0^{+}\) | \(\hat\theta\) | \(SE\) | p-valor (bicaudal) | \(p_{\delta}\) | Conclusão (SGPV) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.350 | 0.550 | -0.100 | 0.100 | 0.450 | 0.0510 | <0,001 | 0.000 | Apoia alternativas (SGPV=0) |
| 2 | -0.050 | 0.080 | -0.100 | 0.100 | 0.015 | 0.0332 | 0.651 | 1.000 | Equivalência (SGPV=1) |
| 3 | -0.500 | 0.700 | -0.100 | 0.100 | 0.100 | 0.3061 | 0.744 | 0.500 | Inconclusivo (0<pδ<1) < td> </pδ<1)> |
| 4 | 0.050 | 0.250 | -0.100 | 0.100 | 0.150 | 0.0510 | 0.003 | 0.250 | Inconclusivo (0<pδ<1) < td> </pδ<1)> |
| 5 | -0.250 | -0.050 | -0.100 | 0.100 | -0.150 | 0.0510 | 0.003 | 0.250 | Inconclusivo (0<pδ<1) < td> </pδ<1)> |
| 6 | 0.150 | 0.550 | -0.100 | 0.100 | 0.350 | 0.1020 | 0.001 | 0.000 | Apoia alternativas (SGPV=0) |
| 7 | -0.550 | -0.150 | -0.100 | 0.100 | -0.350 | 0.1020 | 0.001 | 0.000 | Apoia alternativas (SGPV=0) |
28.6.4 Como interpretar o SGPV?
\(p_{\delta}=0\): dados apoiam apenas hipóteses alternativas relevantes (IC totalmente fora da equivalência).293
\(p_{\delta}=1\): dados apoiam apenas hipóteses nulas (equivalentes) (IC totalmente dentro da equivalência).293 \(0<p_{\delta}<1\): inconclusivo; o valor expressa o grau de inconclusão. Em particular, \(p_{\delta}=\tfrac{1}{2}\) indica inconclusão estrita.293
O SGPV é descritivo (não é probabilidade posterior de \(H_0\)).293
28.6.5 Relação com testes de equivalência (TOST)
Tanto SGPV quanto TOST comparam o IC com os limites de equivalência. Se o IC \((1-2\alpha)\) (p.ex., 90% quando \(\alpha=0{,}05\)) cai inteiro dentro dos limites, TOST conclui equivalência — situação análoga a \(p_{\delta}=1\).294
Com ICs simétricos, há pontos de ancoragem em que as estatísticas coincidem: quando \(p_{\text{TOST}}=0{,}5\), então \(\mathrm{SGPV}=0{,}5\); quando o IC toca o limite mas fica inteiramente dentro (fronteira), \(p_{\text{TOST}}=0{,}025\) e \(\mathrm{SGPV}=1\); quando o IC fica inteiramente fora tocando o limite, \(p_{\text{TOST}}=0{,}975\) e \(\mathrm{SGPV}=0\).294
Em ICs assimétricos ou quando \(|I|>2|H_0|\), o SGPV fica difícil de interpretar quando \(0<p_{\delta}<1\); nesses cenários, o TOST costuma diferenciar melhor os resultados.294
28.6.6 Propriedades frequenciais e múltiplas comparações
Usando ICs \(100(1-\alpha)%\), sob qualquer hipótese em \(H_0\), \(\Pr(p_{\delta}=0)\le \alpha\) e \(\to 0\) com o aumento de \(n\); fora de \(H_0\), \(\Pr(p_{\delta}=0)\to 1\) quando \(n\) cresce.293
O SGPV mitiga naturalmente inflação de erro Tipo I em muitas comparações e prioriza relevância científica (não requer ajustes ad hoc).293
28.7 Distribuição de confiança
28.7.1 O que é distribuição de confiança?
- Distribuição de confiança é uma representação contínua da evidência inferencial sobre um parâmetro de interesse. Ela mostra, para cada valor possível do tamanho do efeito, o nível de confiança associado, sendo uma generalização visual do intervalo de confiança e do P-valor.REF?
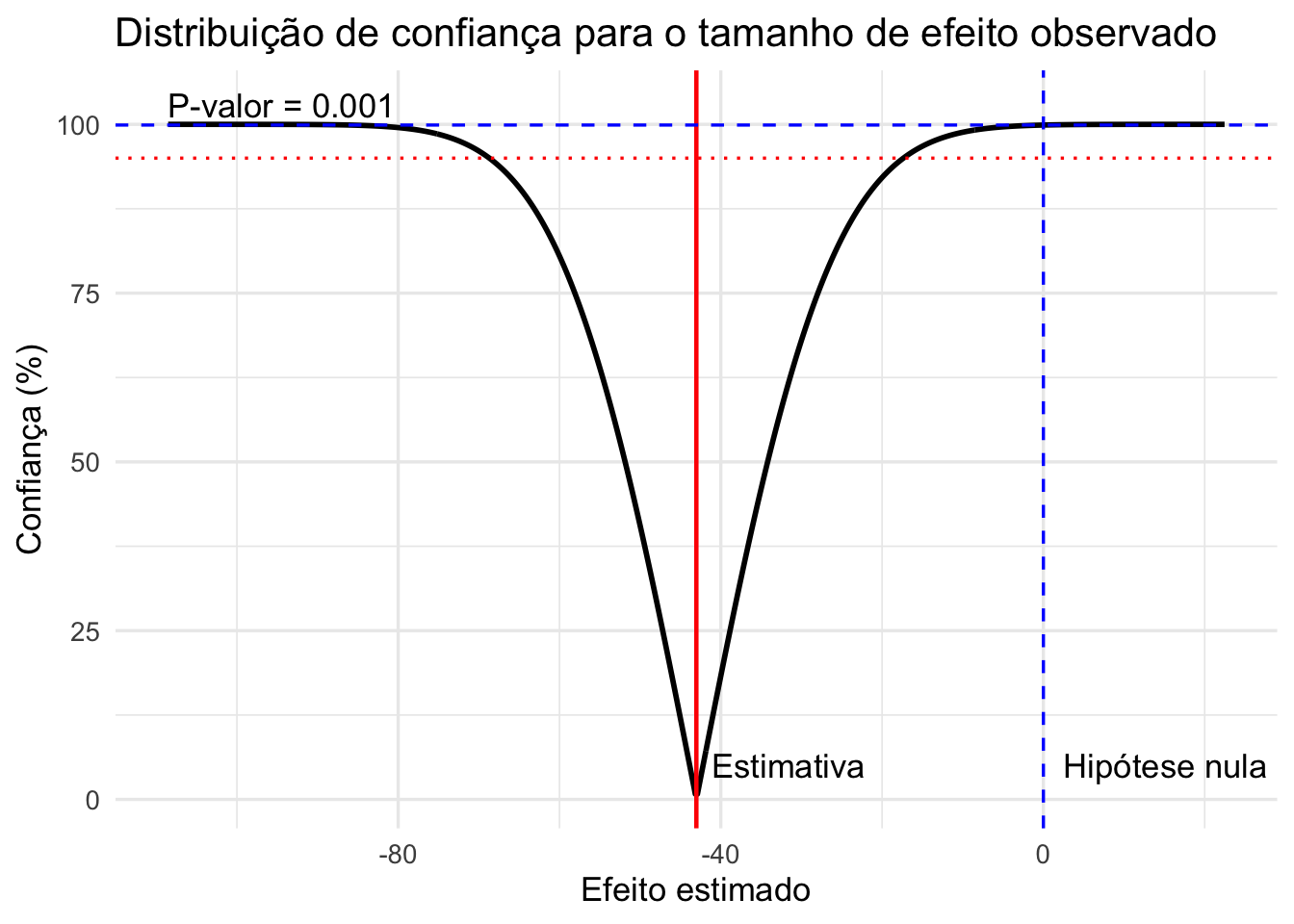
Figura 28.2: Distribuição de confiança para o tamanho do efeito estimado.
28.8 Boas práticas
Defina \(H_0\) intervalar e \(\delta\) a priori com justificativa científica.293,294
Reporte: estimativa pontual, IC, limites de equivalência e \(p_{\delta}\); interprete \(p_{\delta}\in{0,1}\) de forma dicotômica e \(0<p_{\delta}<1\) como inconclusivo; quando necessário, complemente com TOST.293,294
Ferreira, Arthur de Sá. Ciência com R: Perguntas e respostas para pesquisadores e analistas de dados. Rio de Janeiro: 1a edição,