Capítulo 9 Paradoxos estatísticos
9.1 Paradoxos
9.1.1 O que são paradoxos estatísticos?
- Paradoxos podem originar da incompreensão ou mal informação da nossa intuição a respeito do fenômeno.89
9.1.2 O que é o paradoxo de Abelson?
Um baixo percentual de variância explicada não implica que o fator causal seja irrelevante. Em processos cumulativos, efeitos pequenos podem produzir consequências grandes.90
Esse paradoxo alerta contra o uso ingênuo de medidas como \(R^2\) ou “% de explicação” para julgar a importância prática de um fator.REF?
| Variável explicativa | Estimativa | IC 95%1 | P-valor |
|---|---|---|---|
| Nível micro — eventos individuais | |||
| Habilidade | 1.527 | -0.229, 3.282 | 0.088 |
| R² (variância explicada) | 0.001 | ||
| Nível macro — resultado acumulado | |||
| Habilidade | 152.675 | 0.918, 304.432 | 0.049 |
| R² (variância explicada) | 0.199 | ||
| 1 IC = Intervalo de confiança | |||
9.1.10 O que é o paradoxo de Meng?
- Big Data: “Quanto maior a quantidade de dados, maior a certeza de que vamos nos enganar”.89
9.1.12 O que é o paradoxo de Simpson?
O paradoxo de Simpson ocorre quando a associação entre duas variáveis \(X\) e \(Y\) desaparece ou mesmo reverte sua direção quando condicionadas em uma terceira variável \(Z\).99,100
Para decisão do paradoxo de Simpson pode-se utilizar o conceito de back door, o qual considera os caminhos (isto é, associações) no gráfico acíclico direcionado e assegura que todos as associações espúrias do tratamento \(X\) para o desfecho \(Y\) nesse diagrama causal sejam interceptados pela variável \(Z\).101
Dependendo do contexto em que os dados foram obtidos (delineamento do estudo, escolha dos instrumentos e dos tipos de variáveis) a melhor escolha para a análise pode variar entre a análise da população agregada ou da subpopulação desagregada.101
É possível que em alguns contextos nem a análise agregada ou a desagregada podem oferecer a resposta correta, sendo necessário o uso de outras (mais) covariáveis.101
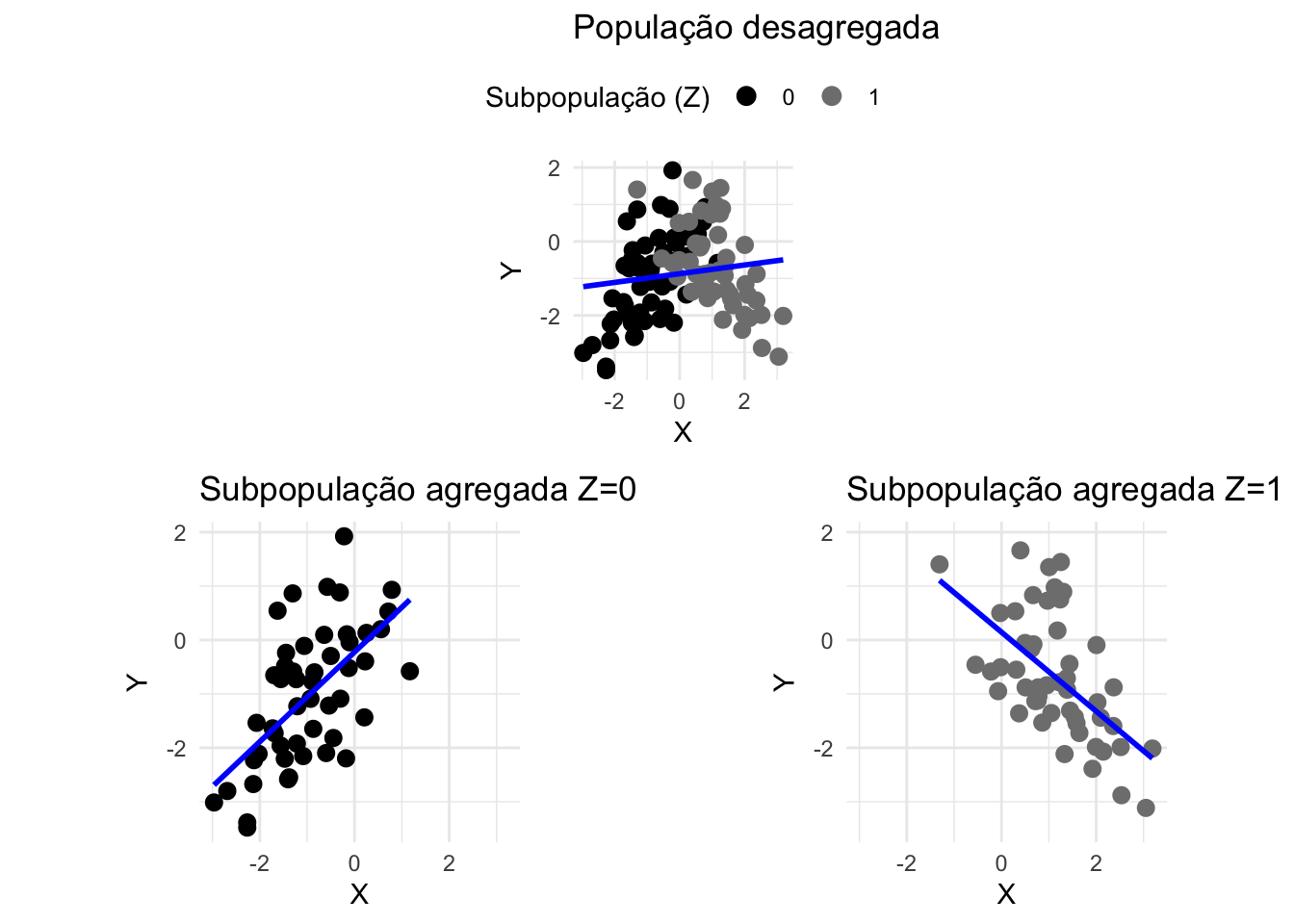
Figura 9.1: Os pontos representam observações individuais e as linhas de tendência representam as regressões lineares ajustadas para os dados desagregados da população e agregados por subpopulação.
9.1.13 O que é o paradoxo de James-Stein?
Ao estimar simultaneamente 3 ou mais médias de variáveis normais independentes (com perda quadrática), o estimador \(X_i\) (ótimo para cada média isoladamente) deixa de ser ótimo no conjunto, existindo estimadores que têm erro médio total menor.102,103
O resultado é paradoxal porque essa melhoria exige “misturar” as estimativas entre si (como no estimador de James–Stein), introduzindo um viés controlado que reduz o erro global, algo impossível quando \(n \leq 2\).102,103
Figura 9.2: Simulação do paradoxo de Stein. Comparação do erro médio quadrático entre o estimador clássico (média amostral) e o estimador de James-Stein para diferentes números de médias (n=2 e n=5). Estimadores aparentemente piores localmente podem ser melhores globalmente quando o objetivo é reduzir o erro total.
9.1.25 O que é o paradoxo da Bela Adormecida?
- .REF?
Ferreira, Arthur de Sá. Ciência com R: Perguntas e respostas para pesquisadores e analistas de dados. Rio de Janeiro: 1a edição,