Capítulo 27 Análise inferencial

27.1 Raciocínio inferencial

27.1.1 O que é análise inferencial?

Na análise inferencial são utilizados dados da(s) amostra(s) para fazer uma inferência válida (isto é, estimativa) sobre os parâmetros populacionais desconhecidos.¹¹¹
No paradigma de Jerzy Neyman e Egon Pearson, um teste de hipótese científica envolve a tomada de decisão sobre hipóteses nulas ($H_{0}$) e alternativa ($H_{1}$) concorrentes e mutuamente exclusivas.²⁶⁵

27.1.2 Quais são os tipos de raciocínio inferencial?

Inferência dedutiva: Uma dada hipótese inicial é utilizada para prever o que seria observado caso tal hipótese fosse verdadeira.²⁶⁶
Inferência indutiva: Com base nos dados observados, avalia-se qual hipótese é mais defensável (isto é, mais provável).²⁶⁶

27.1.3 Quais são as questões fundamentais da análise inferencial?

A direção do efeito²⁶⁷
A magnitude do efeito²⁶⁷
A importância do efeito²⁶⁷

27.2 Hipóteses científicas

27.2.1 O que é hipótese científica?

Hipótese científica é uma ideia que pode ser testada.²⁶⁵
Definir claramente os problemas e os objetivos da pesquisa são o ponto de partida de todos os estudos científicos.¹³⁶
Além do papel técnico, os testes de hipótese carregam uma dimensão interpretativa que molda como os pesquisadores comunicam descobertas. Estudos recentes destacam o caráter pragmático e dicotômico dessas decisões.²⁶⁸

27.2.2 Quais são as fontes de ideias para gerar hipóteses científicas?

Revisão das práticas atuais.²⁶⁹
Desafio a ideias aceitas.²⁶⁹
Conflito entre ideias divergentes.²⁶⁹
Variações regionais, temporais e populacionais.²⁶⁹
Experiências dos próprios pesquisadores.²⁶⁹
Imaginação sem fronteiras ou limites convencionais.²⁶⁹

27.3 Hipóteses estatísticas

27.3.1 O que é hipótese nula?

A hipótese nula ($H_{0}$) é uma expressão que representa o estado atual do conhecimento (status quo), em geral a não existência de um determinado efeito.¹⁸³

27.3.2 O que é hipótese alternativa?

A hipótese alternativa ($H_{1}$) é uma expressão que contém as situações que serão testadas, de modo que um resultado positivo indique alguma ação a ser conduzida.¹⁸³

27.3.3 Qual hipótese está sendo testada?

A hipótese nula ($H_{0}$) é a hipótese sob teste em análises inferenciais.¹¹²
Pode-se concluir sobre rejeitar ou não rejeitar a hipótese nula ($H_{0}$).¹¹²
Não se conclui sobre a hipótese alternativa ($H_{1}$).¹⁸³
Para testar a hipótese nula, deve-se selecionar o nível de significância crítica (P-valor de corte); a probabilidade de rejeitarmos uma hipótese nula verdadeira ($\alpha$); e a probabilidade de não rejeitarmos uma hipótese nula falsa ($\beta$).²⁶⁵

27.4 Testes de hipóteses

27.4.1 Quais são os tipos de teste de hipóteses?

Teste (clássico) de significância da hipótese nula: verifica evidência contra $H_{0}$ usando P-valor.²⁷⁰
Teste de mínimos efeitos (MOTE/MOST/SESOI): testa se o efeito é pelo menos tão grande quanto um limiar de relevância (SESOI). Rejeitar $H_{0}$ sugere efeito grande o suficiente.²⁷⁰
Teste de equivalência (TOST): testa se o efeito está dentro de uma margem de equivalência clinicamente irrelevante (entre $\Delta$ e $-\Delta$). Rejeitar $H_{0}$ sugere equivalência prática.²⁷⁰
Teste de superioridade: avalia se um tratamento/intervenção supera o controle por uma margem $>0$ ou $>\Delta$.²⁷⁰
Teste de não-inferioridade: avalia se o tratamento não é pior que o controle por mais do que $-\Delta$.^REF?
Teste de inferioridade: avalia se o tratamento é pior que o controle (por exemplo, para checar segurança).^REF?

27.4.2 O que reportar após um teste de hipótese?

P-valores, como estimativa da significância estatística.²⁷¹
Tamanho do efeito, como estimativa de significância substantiva.²⁷¹

27.5 Intervalos de confiança e raciocínio de longo prazo

27.5.1 O que é um intervalo de confiança?

Um intervalo de confiança é um procedimento inferencial utilizado para estimar um parâmetro populacional desconhecido a partir de dados amostrais, levando em conta a variabilidade inerente ao processo de amostragem.²⁷²
Diferentemente de uma estatística descritiva, o intervalo de confiança não é uma propriedade fixa do parâmetro, mas uma propriedade do procedimento estatístico utilizado para estimá-lo.²⁷³
O parâmetro populacional é considerado fixo (embora desconhecido), enquanto o intervalo de confiança é uma quantidade aleatória, pois depende da amostra observada.^REF?

27.5.2 Intervalos de confiança e a lógica frequentista

No paradigma frequentista, a probabilidade é interpretada como uma frequência relativa observável no longo prazo, associada a um processo repetível.²⁷²
Um intervalo de confiança de nível $(1-\alpha)$ é construído de modo que, se o mesmo procedimento de amostragem e análise fosse repetido indefinidamente sob as mesmas condições, aproximadamente $(1-\alpha)\times100\%$ dos intervalos assim gerados conteriam o verdadeiro valor do parâmetro populacional.²⁷³
Portanto, a probabilidade associada ao intervalo de confiança refere-se ao desempenho do procedimento no longo prazo, e não à probabilidade de o parâmetro estar contido em um intervalo específico observado.

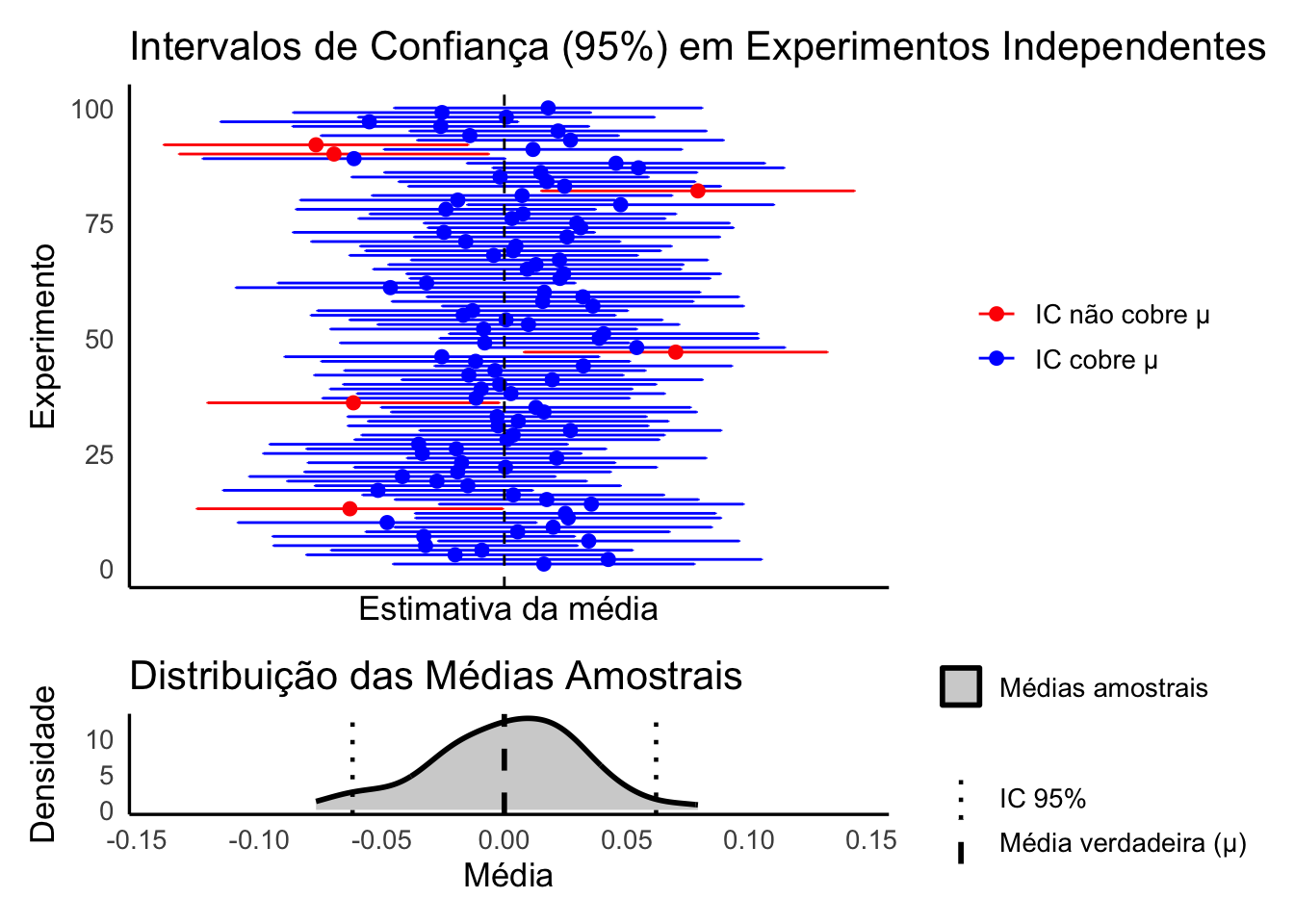
$Simulação ilustrativa de intervalos de confiança (IC) em 100 experimentos independentes, cada um com 1.000 observações amostradas de uma população normal padrão (média = 0, desvio-padrão = 1). Os ICs são construídos no nível de 95\%. O gráfico superior mostra os ICs individuais para cada experimento, indicando se o IC cobre ou não a média verdadeira ($\mu = 0$). O gráfico inferior apresenta a distribuição das médias amostrais obtidas nos experimentos, juntamente com o IC teórico para a média populacional. Observe que aproximadamente 95\% dos ICs individuais cobrem a média verdadeira, ilustrando o conceito de cobertura no longo prazo associado aos intervalos de confiança.$

Figura 27.1: Simulação ilustrativa de intervalos de confiança (IC) em 100 experimentos independentes, cada um com 1.000 observações amostradas de uma população normal padrão (média = 0, desvio-padrão = 1). Os ICs são construídos no nível de 95%. O gráfico superior mostra os ICs individuais para cada experimento, indicando se o IC cobre ou não a média verdadeira ($\mu = 0$). O gráfico inferior apresenta a distribuição das médias amostrais obtidas nos experimentos, juntamente com o IC teórico para a média populacional. Observe que aproximadamente 95% dos ICs individuais cobrem a média verdadeira, ilustrando o conceito de cobertura no longo prazo associado aos intervalos de confiança.

27.5.3 O que um intervalo de confiança não representa

Um intervalo de confiança não deve ser interpretado como a probabilidade de que o parâmetro esteja contido naquele intervalo específico.²⁷⁴
Após os dados terem sido observados e o intervalo calculado, o parâmetro populacional ou está dentro do intervalo ou não está; não há incerteza probabilística sobre isso no sentido frequentista.²⁷⁴
A incerteza expressa pelo intervalo de confiança refere-se à variabilidade do processo inferencial, e não a uma distribuição de probabilidade do parâmetro.²⁷⁴

27.5.4 Relação entre intervalos de confiança e testes de hipóteses

Intervalos de confiança e testes de hipótese frequentistas são derivados do mesmo modelo probabilístico subjacente e utilizam as mesmas suposições estatísticas.²⁷⁵
Em testes bicaudais, qualquer valor hipotético do parâmetro que esteja fora do intervalo de confiança de nível $(1-\alpha)$ corresponde a uma hipótese nula que seria rejeitada ao nível de significância $\alpha$.²⁷⁵
De forma análoga, valores do parâmetro que estejam dentro do intervalo de confiança correspondem a hipóteses nulas para as quais não haveria evidência suficiente para rejeição ao nível $\alpha$.²⁷⁵
Apesar dessa equivalência formal, intervalos de confiança e testes de hipótese respondem a perguntas distintas: testes enfatizam decisões dicotômicas, enquanto intervalos de confiança enfatizam estimação e incerteza.²⁷⁵

27.5.5 Por que intervalos de confiança são centrais na inferência científica

Intervalos de confiança permitem avaliar simultaneamente a magnitude do efeito e a incerteza associada à sua estimativa, na mesma unidade de medida da variável de interesse.²⁷⁵
Essa abordagem favorece interpretações substantivas e científicas dos resultados, em oposição a decisões puramente dicotômicas baseadas em pontos de corte arbitrários.²⁷⁵
Quando corretamente interpretados, intervalos de confiança promovem uma comunicação mais informativa da evidência científica e reduzem interpretações equivocadas associadas ao uso exclusivo de P-valores.²⁷⁴

27.6 Comparações múltiplas

27.6.1 O que é uma família de hipóteses?

Família de hipóteses é um conjunto de comparações/inferências que, por desenho ou análise, devem ser consideradas juntas para controle do erro tipo I global (ex.: todas as comparações de um desfecho primário, todos os subgrupos pré-especificados, todos os desfechos coprimários).^REF?
O controle do family-wise error rate (FWER) ou do false discovery rate (FDR) deve considerar a família pertinente, não comparações isoladas.^REF?

27.6.2 O que são testes ad hoc e post hoc?

Ad hoc: análises/decisões não planejadas a priori, motivadas por inspeção dos dados. Úteis para gerar hipóteses, não para confirmá-las.^REF?
Post hoc: procedimentos de comparações múltiplas aplicados após um teste global ter indicado efeito significativo. Visam controlar o erro tipo I em múltiplas comparações.^REF?

27.6.3 Como ajustar a análise inferencial para hipóteses múltiplas?

Defina a família (o que entra no ajuste) e priorize desfechos (primário, coprimários, secundários).^REF?
Aplique métodos de controle FWER (Bonferroni, Holm, Hochberg, Dunnett para múltiplos vs. controle) ou controle FDR (Benjamini–Hochberg) conforme o objetivo (confirmação vs. exploração).^REF?
Em planos confirmatórios, use hierarquização/gatekeeping: testa-se em sequência; a alocação de $\alpha$ passa adiante apenas se houver significância no nível anterior.^REF?

O pacote stats¹³⁴ fornece a função p.adjust para ajustar o P-valor utilizando diversos métodos.

27.6.4 O que são testes unicaudais e bicaudais?

Teste unicaudal procura evidência em uma direção específica (ex.: “maior que 0”). Toda a região crítica está numa só cauda; tem maior poder para aquela direção, mas não detecta sinal oposto.^REF?

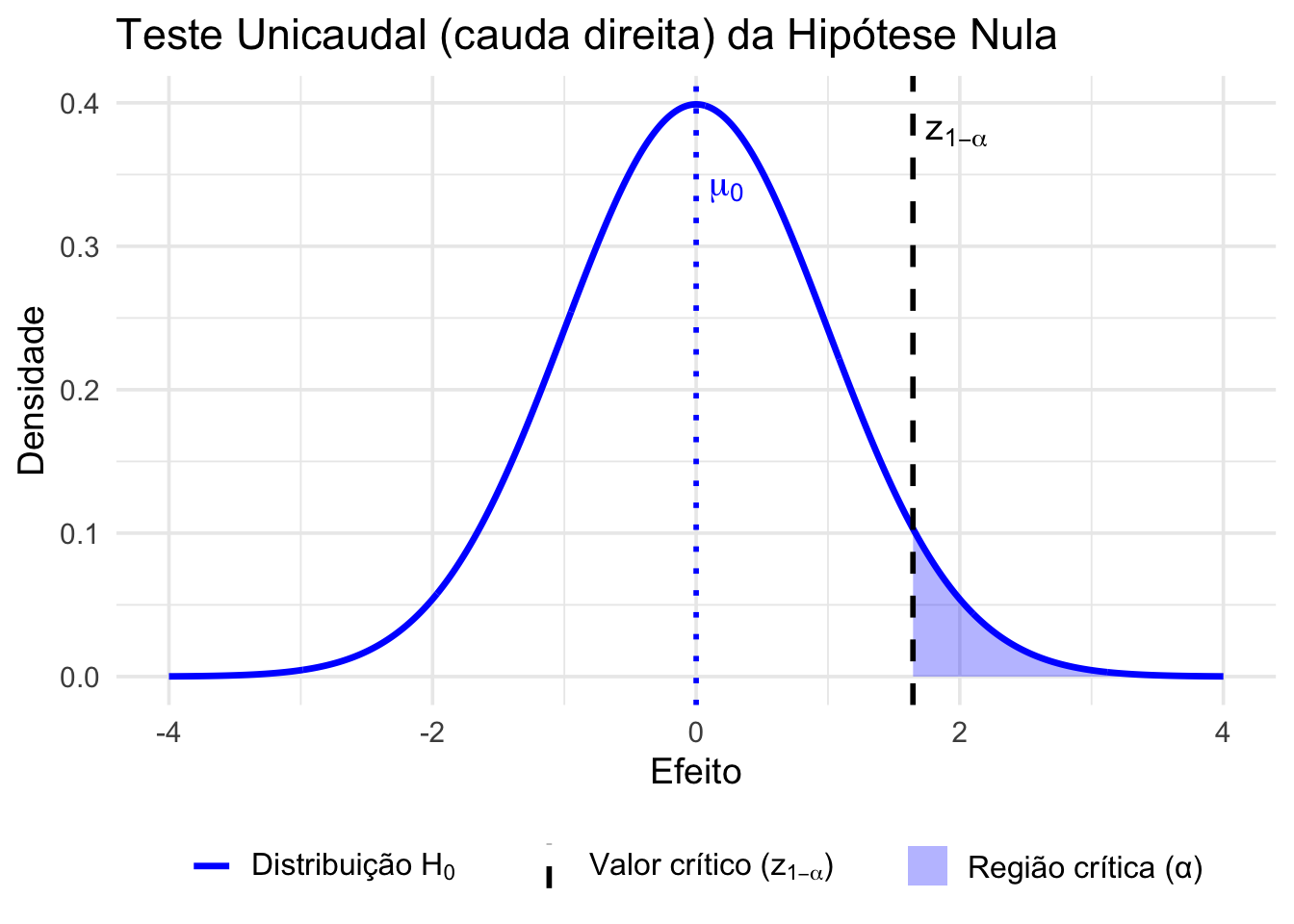
Representação gráfica de um teste de hipótese unicaudal à direita, aplicado quando se busca evidência de efeitos positivos (valores significativamente maiores que o esperado sob $H_0$).

Figura 27.2: Representação gráfica de um teste de hipótese unicaudal à direita, aplicado quando se busca evidência de efeitos positivos (valores significativamente maiores que o esperado sob $H_0$).

Representação gráfica de um teste de hipótese unicaudal à esquerda, aplicado quando se busca evidência de efeitos negativos (valores significativamente menores que o esperado sob $H_0$).

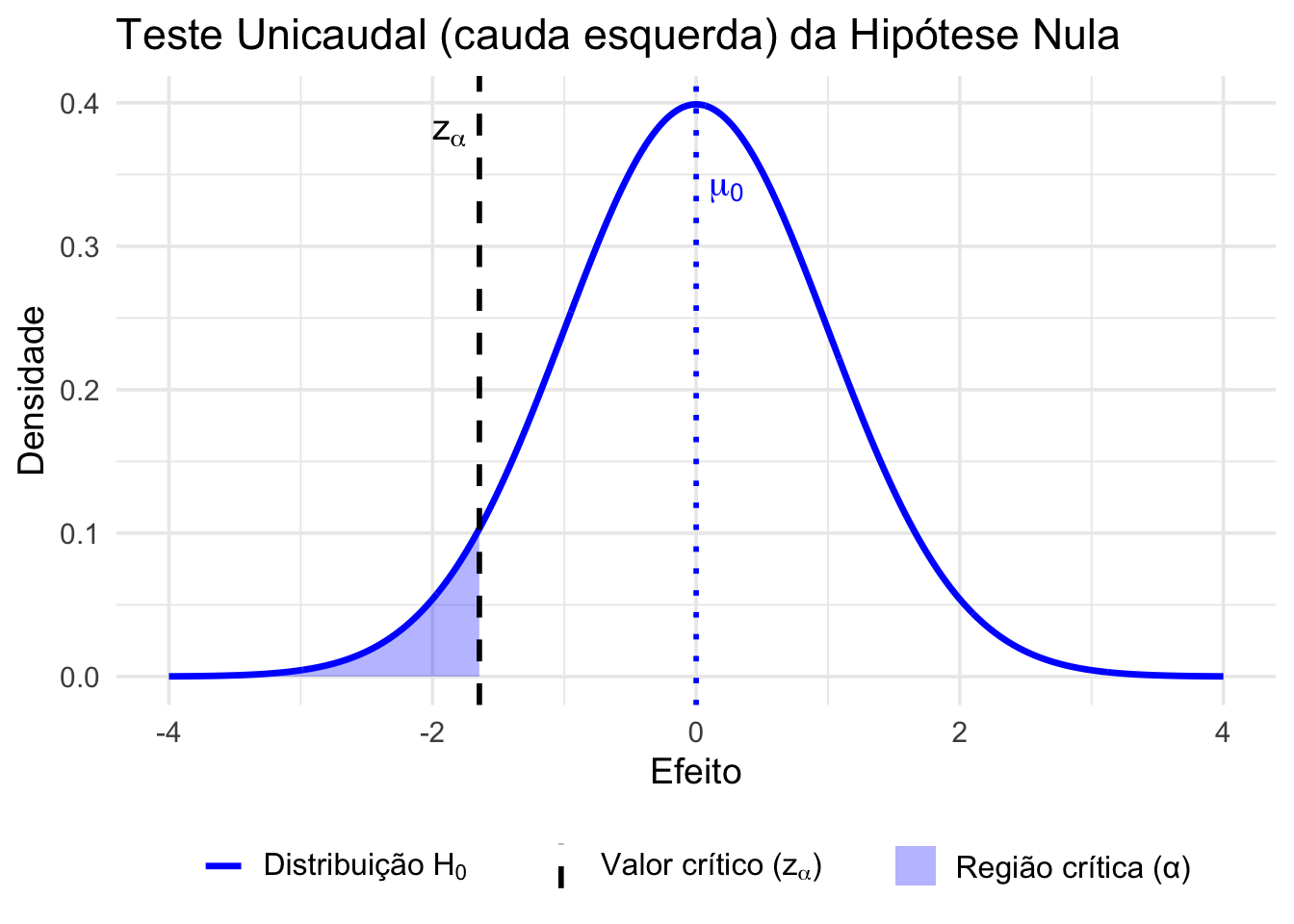
Figura 27.3: Representação gráfica de um teste de hipótese unicaudal à esquerda, aplicado quando se busca evidência de efeitos negativos (valores significativamente menores que o esperado sob $H_0$).

Teste bicaudal procura evidência em qualquer direção (ex.: “diferente de 0”). Divide $\alpha$ em duas caudas (direita e esquerda). É a escolha padrão quando ambas as direções são plausíveis.^REF?

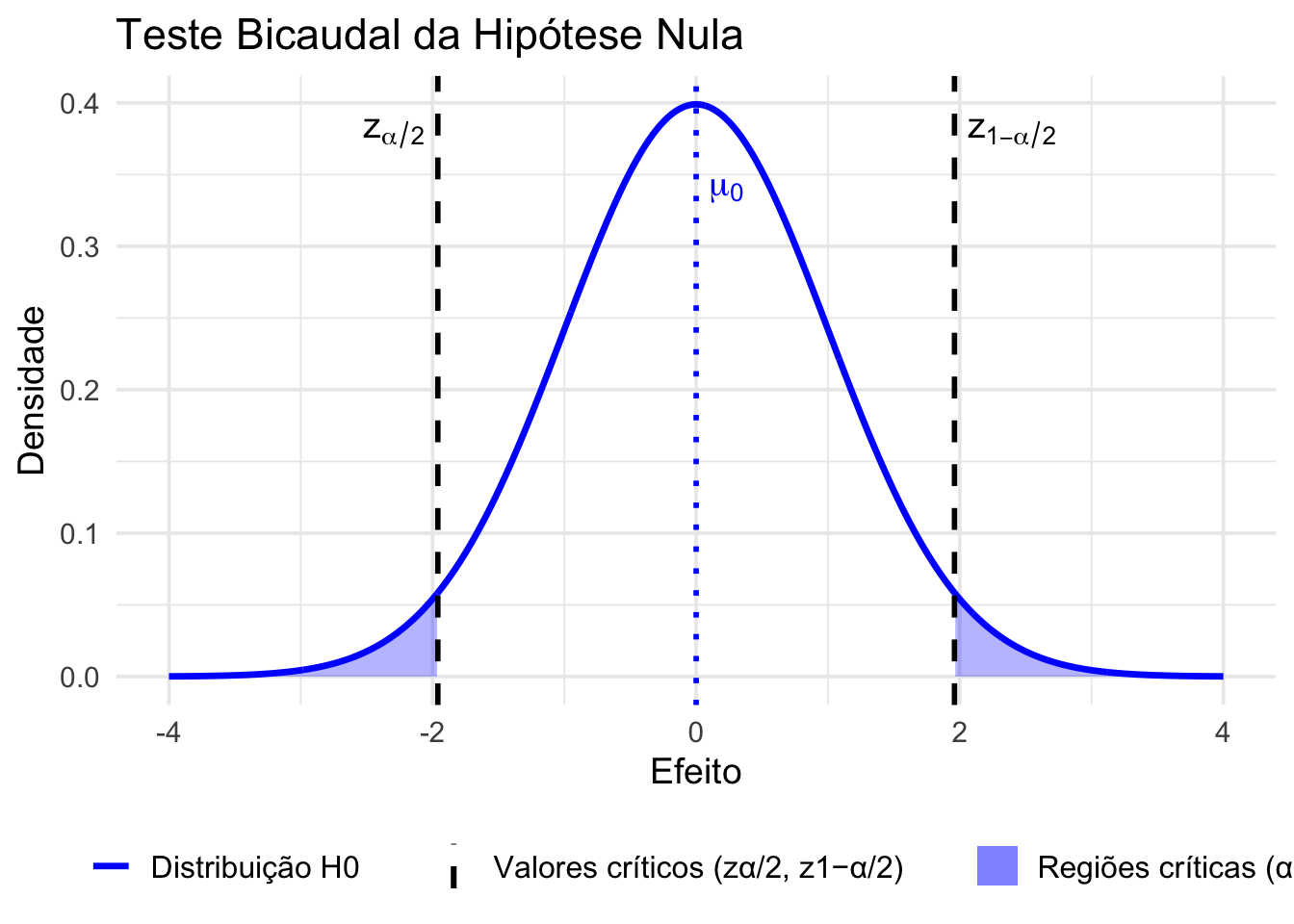
Representação gráfica de um teste de hipótese bicaudal, aplicado quando se busca evidência de efeitos positivos ou negativos (valores significativamente diferentes do esperado sob $H_0$).

Figura 27.4: Representação gráfica de um teste de hipótese bicaudal, aplicado quando se busca evidência de efeitos positivos ou negativos (valores significativamente diferentes do esperado sob $H_0$).

27.7 Inferência visual

27.7.1 O que é inferência visual?

Inferência visual consiste na interpretação de dados apresentados em gráficos.²⁷⁵
Para inferência visual, recomenda-se a apresentação dos dados em gráficos com estimativas de tendência central e seu intervalo (preferencialmete intervalo de confiança no nível de significância $\alpha$ pré-estabelecido).²⁷⁵

27.7.2 Por que usar intervalos de confiança para inferência visual?

Intervalos de confiança fornecem estimativas pontuais e intervalares na mesma unidade de medida da variável.²⁷⁵
Existe uma relação entre o intervalo de confiança e o P-valor obtido pelo teste de significância de hipótese nula $H_{0}$, em que ambos consideram o mesmo nível de significância $\alpha$ pré-estabelecido.²⁷⁵

27.7.3 Como interpretar intervalos de confiança em uma figura?

Identifique o que as tendências centrais e as barras de erro representam. Qual é a variável dependente? É expressa em unidades originais ou é padronizada ? A figura mostra intervalos de confiança, erro-padrão ou desvio-padrão? Qual é o desenho experimental?²⁷⁵
Faça uma interpretação substantiva dos valores de tendência central e dos intervalos de confiança.²⁷⁵
O intervalo de confiança é uma faixa de valores plausíveis para a tendência central. Valores fora do intervalo são relativamente implausíveis, no nível de significância $\alpha$ pré-estabelecido.²⁷⁵
Qualquer valor fora do intervalo de confiança, quando considerado como hipótese nula ($H_{0}$), equivale a $P < \alpha$ pré-estabelecido (bicaudal).²⁷⁵
Qualquer valor dentro do intervalo, quando considerado como hipótese nula ($H_{0}$), equivale a $P > \alpha$ pré-estabelecido (bicaudal).²⁷⁵

27.8 Interpretação de análise inferencial

27.8.1 Como interpretar uma análise inferencial?

Testes de hipótese nula ($H_{0}$) vs. alternativa ($H_{1}$) a partir de um nível de significância ($\alpha$) pré-especificado.²⁷³
P-valor como evidência estatística sobre ($H_{0}$).²⁷³
Estimação de intervalos de confiança de um nível de significância ($\alpha$) pré-especificado bicaudal ($IC_{1-\alpha/2}$) ou unicaudal ($IC_{1-\alpha}$).²⁷³
Análise Bayesiana.²⁷³

27.8.2 O que são resultados positivos” e “negativos” (inconclusivos) em teste de hipótese?

Resultados “positivos” compreendem um P-valor dentro da zona crítica estatisticamente significativa (ex.: $P<0,05$ ou outro ponto de corte) e sugerem que os autores rejeitem a hipótese nula ($H_{0}$), confirmando assim sua hipótese científica.²⁷⁶
Resultados “negativos” ou inconclusivos compreendem um P-valor fora da zona crítica estatisticamente significativa (ex.: $P \geq 0,05$ ou outro ponto de corte) e sugerem que os autores não rejeitem a hipótese nula ($H_{0}$) porque o efeito observado é nulo (logo, “negativo”), ou porque o estudo não possui poder suficiente para detectá-lo, não permitindo portanto afirmar a hipótese científica (logo, inconclusivo).²⁷⁶

27.8.3 Qual a importância de resultados “negativos”?

Conhecer resultados negativos contribui com uma visão mais ampla do campo de estudo junto aos resultados positivos.²⁷⁷
Resultados negativos permitem um melhor planejamento das pesquisas futuras e pode aumentar suas chances de sucesso.²⁷⁷

27.8.4 Resultados inconclusivos: Ausência de evidência ou evidência de ausência?

Em estudos (geralmente com amostras grandes), resultados estatisticamente significativos (com P-valores menores do limiar pré-estabelecido, $P<\alpha$) podem não ser clinicamente relevantes.²⁷⁸
Em estudos (geralmente com amostras pequenas), resultados estatisticamente não significativos (com P-valores iguais ou maiores do limiar pré-estabelecido, $P \geq \alpha$) não devem ser interpretados como evidência de inexistência do efeito.²⁷⁸
Geralmente é razoável aceitar uma nova conclusão apenas quando há dados a seu favor (‘resultados positivos’). Também é razoável questionar se apenas a ausência de dados a seu favor (‘resultados negativos’) justifica suficientemente a rejeição de tal conclusão.²⁷⁸
A prática estatística convencional tende a reduzir a incerteza científica a decisões docotômicas. Essa simplificação possui implicações epistemológicas importantes: os testes de hipótese produzem não apenas juízos empíricos, mas também atos pragmáticos que comunicam graus de confiança e orientam ações.²⁶⁸

27.9 Erros de inferência I, II, S e M

27.9.1 O que são erros de inferência estatística?

Um erro de inferência é a tomada de decisão incorreta, seja a favor ou contra a hipótese nula ($H_{0}$).²⁶⁵

27.9.2 O que são erros Tipo I e Tipo II?

Erro Tipo I significa a rejeição de uma hipótese nula ($H_{0}$) quando esta é verdadeira.²⁶⁵
Erro Tipo II significa a não rejeição de uma hipótese nula ($H_{0}$) quando esta é falsa.²⁶⁵

Tabela 27.1: Tabela de erros tipos I e II de inferência estatística.
	Hipótese nula $H_{0}$ é falsa	Hipótese nula $H_{0}$ é verdadeira
Hipótese nula $H_{0}$ foi rejeitada	Decisão correta	Decisão incorreta (erro tipo I)
Hipótese nula $H_{0}$ não foi rejeitada	Decisão incorreta (erro tipo II)	Decisão correta

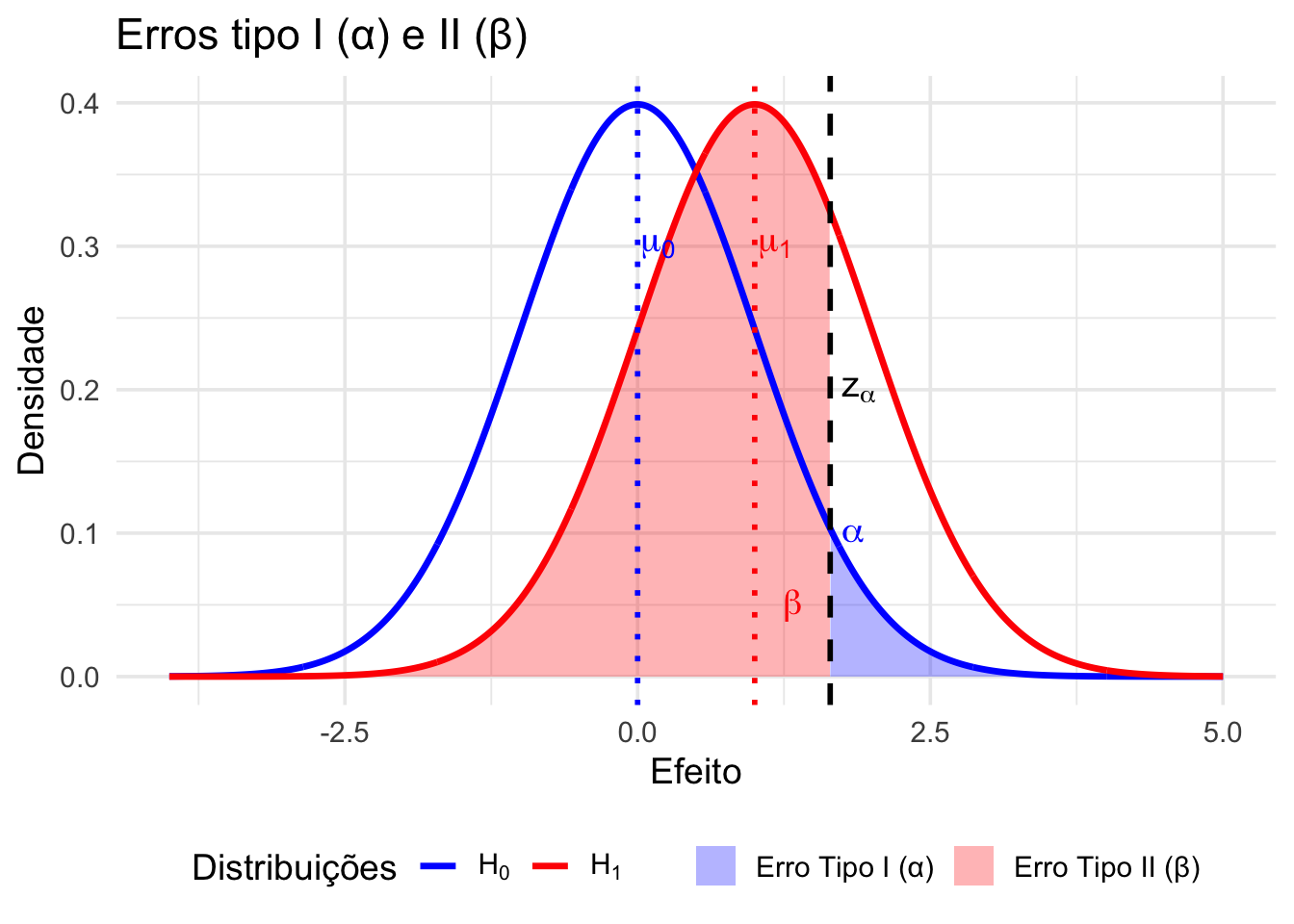
Figura 27.5: Representação gráfica dos erros tipo I e tipo II em um teste de hipótese (bicaudal).

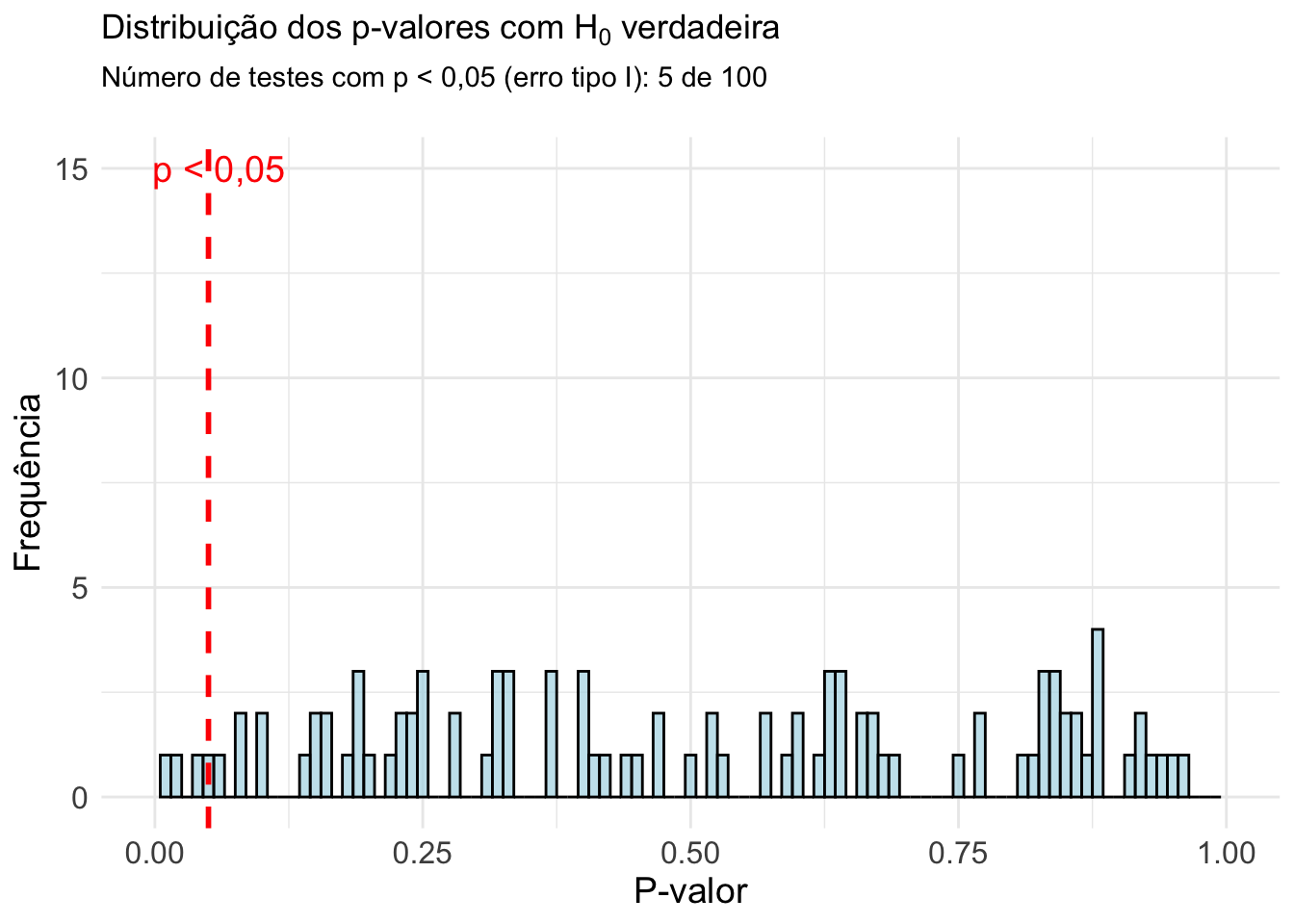
Erro tipo I: Distribuição dos p-valores em 100 testes de hipótese de amostras aleatórias de tamanho 30. A linha vermelha pontilhada indica o nível de significância estatística de 0,05.

Figura 27.6: Erro tipo I: Distribuição dos p-valores em 100 testes de hipótese de amostras aleatórias de tamanho 30. A linha vermelha pontilhada indica o nível de significância estatística de 0,05.

Erro tipo II: Distribuição dos p-valores em 100 testes de hipótese de amostras aleatórias de tamanho 10. A linha vermelha pontilhada indica o nível de significância estatística de 0,05.

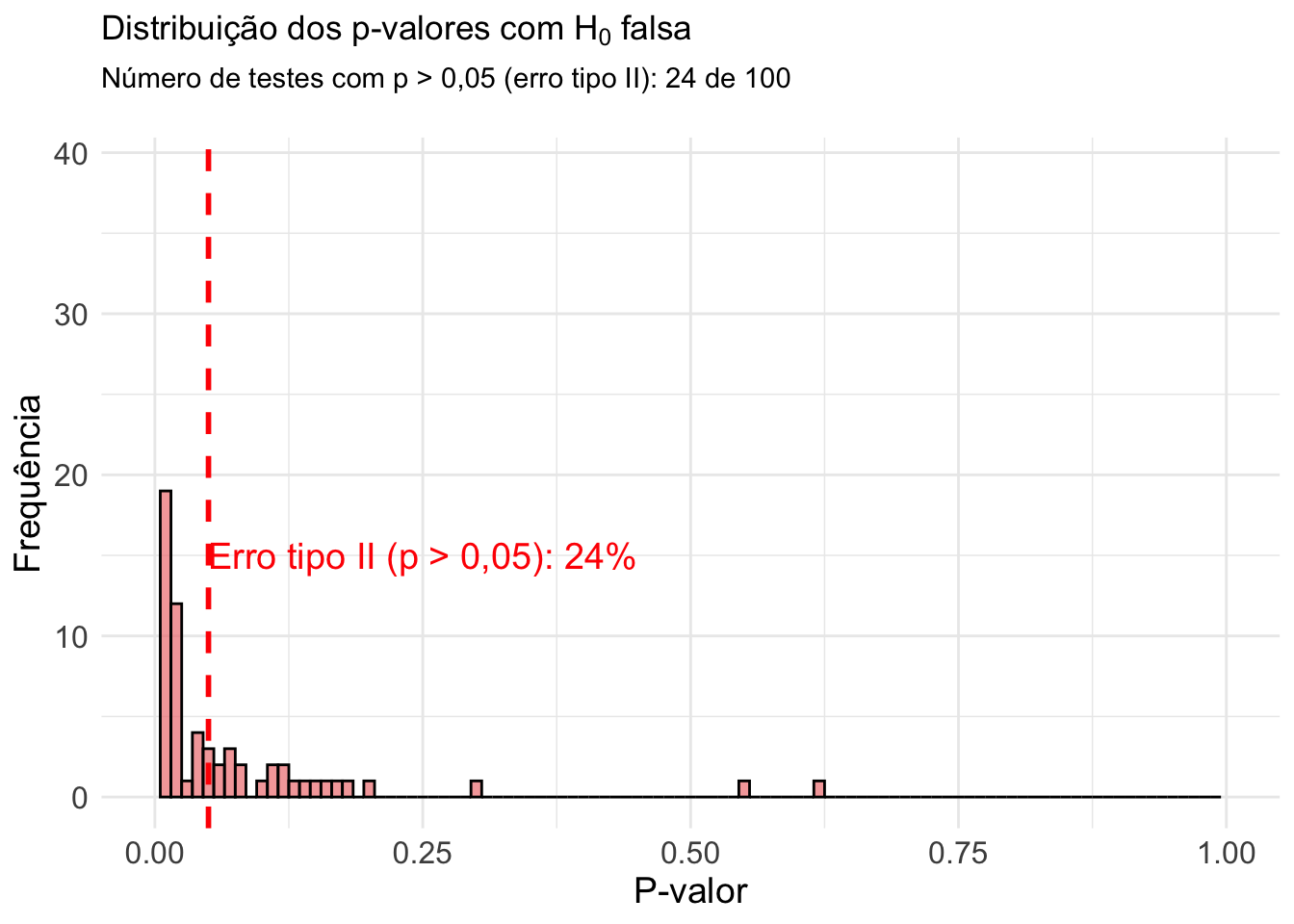
Figura 27.7: Erro tipo II: Distribuição dos p-valores em 100 testes de hipótese de amostras aleatórias de tamanho 10. A linha vermelha pontilhada indica o nível de significância estatística de 0,05.

27.9.3 O que são erros Tipo S e Tipo M?

Erro Tipo S (do inglês sign) significa a identificação errônea da direção — positiva ou negativa — do efeito observado.^279,280

Tabela 27.2: Tabela de erro tipo S de inferência estatística.
	Sinal positivo	Sinal negativo
Sinal positivo	Decisão correta	Decisão incorreta (erro tipo S)
Sinal negativo	Decisão incorreta (erro tipo S)	Decisão correta

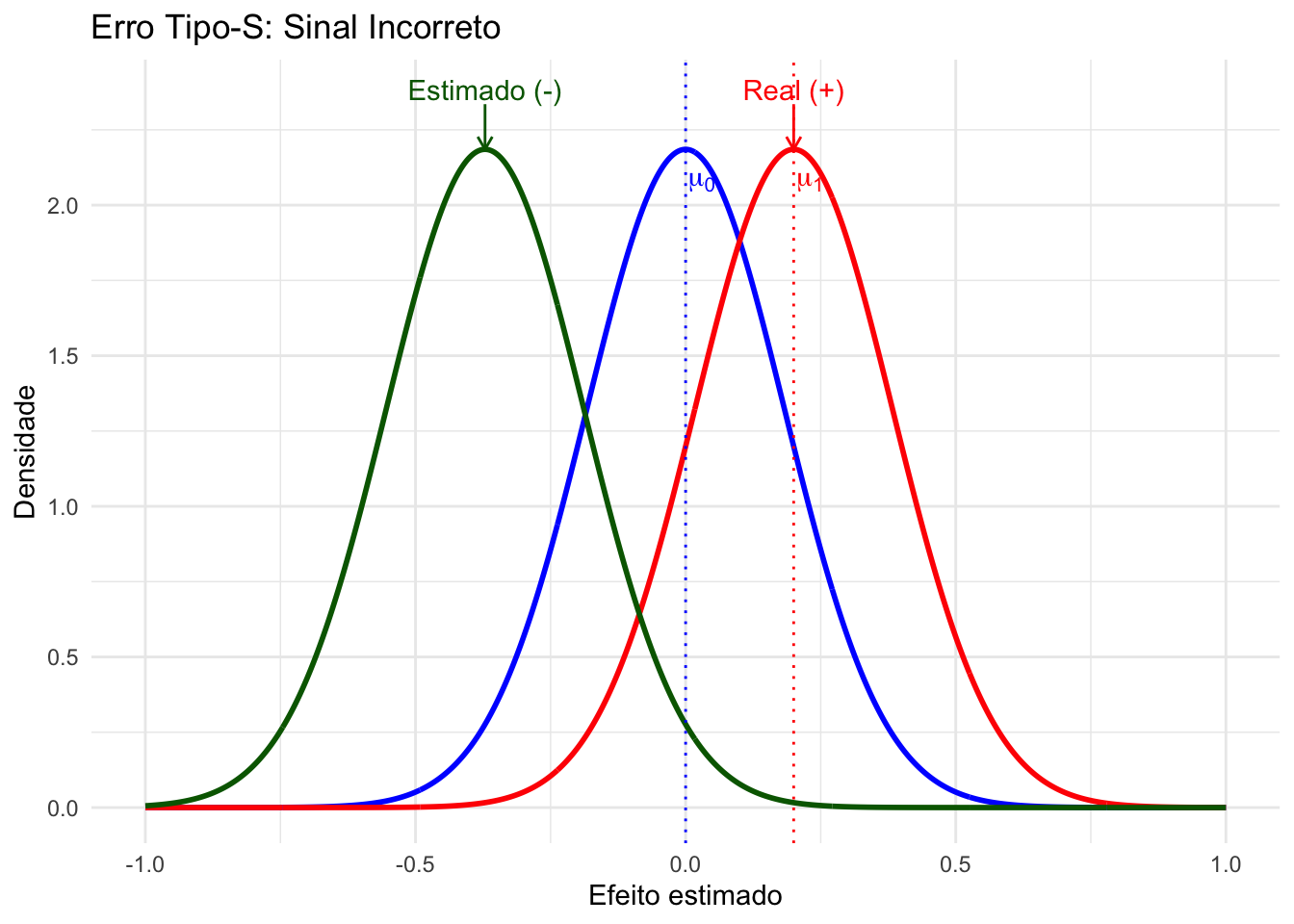
Figura 27.8: Representação gráfica do erro tipo S (sinal) em um teste de hipótese (bicaudal).

Erro Tipo M (do inglês magnitude) significa a identificação errônea — em geral, exagerada — da magnitude do efeito observado.^279,280

Tabela 27.3: Tabela de erro tipo M de inferência estatística.
	Magnitude alta	Magnitude baixa
Magnitude alta	Decisão correta	Decisão incorreta (erro tipo M)
Magnitude baixa	Decisão incorreta (erro tipo M)	Decisão correta

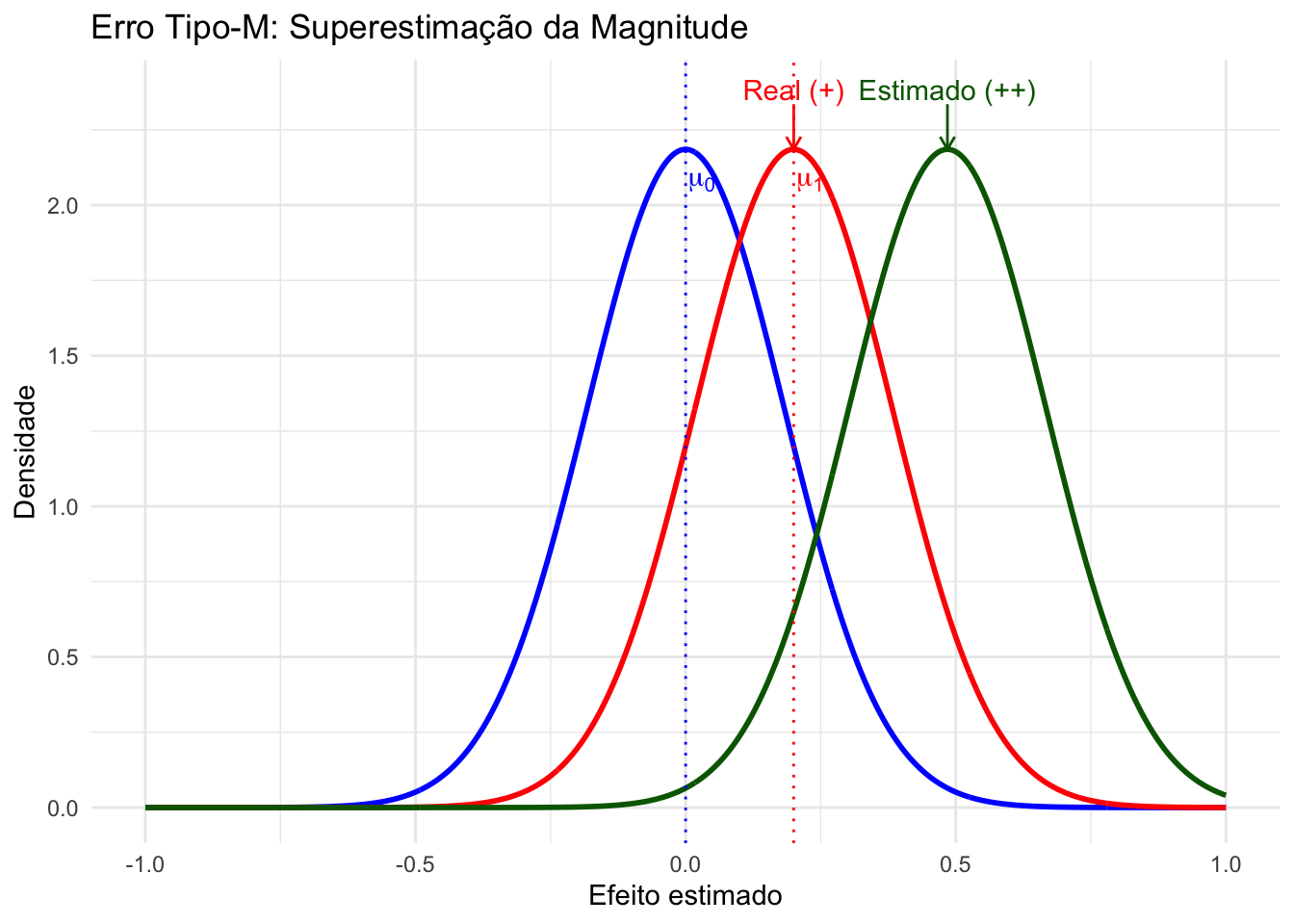
Figura 27.9: Representação gráfica do erro tipo M (magnitude) em um teste de hipótese (bicaudal).

Citar como:
Ferreira, Arthur de Sá. Ciência com R: Perguntas e respostas para pesquisadores e analistas de dados. Rio de Janeiro: 1a edição,

Referências

111.

Vetter TR. Fundamentals of Research Data and Variables. Anesthesia & Analgesia. 2017;125(4):1375–1380. doi:10.1213/ane.0000000000002370

112.

Ali Z, Bhaskar Sb. Basic statistical tools in research and data analysis. Indian Journal of Anaesthesia. 2016;60(9):662. doi:10.4103/0019-5049.190623

134.

R Core Team. R: A Language and Environment for Statistical Computing.; 2025. https://www.R-project.org/.

136.

Smeden M van. A Very Short List of Common Pitfalls in Research Design, Data Analysis, and Reporting. PRiMER. 2022;6. doi:10.22454/PRiMER.2022.511416

183.

Kanji G. 100 Statistical Tests. SAGE Publications Ltd; 2006. doi:10.4135/9781849208499

265.

Curran-Everett D. Explorations in statistics: hypothesis tests and P values. Advances in Physiology Education. 2009;33(2):81–86. doi:10.1152/advan.90218.2008

266.

Goodman SN. Toward Evidence-Based Medical Statistics. 1: The P Value Fallacy. Annals of Internal Medicine. 1999;130(12):995. doi:10.7326/0003-4819-130-12-199906150-00008

267.

McCaskey K, Rainey C. Substantive Importance and the Veil of Statistical Significance. Statistics, Politics and Policy. 2015;6(1-2). doi:10.1515/spp-2015-0001

269.

Vandenbroucke JP, Pearce N. From ideas to studies: how to get ideas and sharpen them into research questions. Clinical Epidemiology. 2018;Volume 10:253–264. doi:10.2147/clep.s142940

270.

Lakens D, Scheel AM, Isager PM. Equivalence Testing for Psychological Research: A Tutorial. Advances in Methods and Practices in Psychological Science. 2018;1(2):259–269. doi:10.1177/2515245918770963

271.

Sullivan GM, Feinn R. Using Effect Sizeor Why the P Value Is Not Enough. Journal of Graduate Medical Education. 2012;4(3):279–282. doi:10.4300/jgme-d-12-00156.1

272.

Neyman J. Outline of a Theory of Statistical Estimation Based on the Classical Theory of Probability. Philosophical Transactions of the Royal Society of London Series A, Mathematical and Physical Sciences. 1937;236(767):333–380. doi:10.1098/rsta.1937.0005

273.

Goodman SN. Aligning statistical and scientific reasoning. Science. 2016;352(6290):1180–1181. doi:10.1126/science.aaf5406

274.

Greenland S, Senn SJ, Rothman KJ, et al. Statistical tests, P values, confidence intervals, and power: a guide to misinterpretations. European Journal of Epidemiology. 2016;31(4):337–350. doi:10.1007/s10654-016-0149-3

275.

Cumming G, Finch S. Inference by Eye: Confidence Intervals and How to Read Pictures of Data. American Psychologist. 2005;60(2):170–180. doi:10.1037/0003-066x.60.2.170

276.

Greenhalgh T. How to read a paper: Statistics for the non-statistician. II: ̈Significanẗ relations and their pitfalls. BMJ. 1997;315(7105):422–425. doi:10.1136/bmj.315.7105.422

277.

Weintraub PG. The Importance of Publishing Negative Results. Journal of Insect Science. 2016;16(1):109. doi:10.1093/jisesa/iew092

278.

Altman DG, Bland JM. Statistics notes: Absence of evidence is not evidence of absence. BMJ. 1995;311(7003):485–485. doi:10.1136/bmj.311.7003.485

279.

Gelman A, Carlin J. Beyond Power Calculations. Perspectives on Psychological Science. 2014;9(6):641–651. doi:10.1177/1745691614551642

280.

Lu J, Qiu Y, Deng A. A note on Type S/M errors in hypothesis testing. British Journal of Mathematical and Statistical Psychology. 2018;72(1):1–17. doi:10.1111/bmsp.12132

	Hipótese nula \(H_{0}\) é falsa	Hipótese nula \(H_{0}\) é verdadeira
Hipótese nula \(H_{0}\) foi rejeitada	Decisão correta	Decisão incorreta (erro tipo I)
Hipótese nula \(H_{0}\) não foi rejeitada	Decisão incorreta (erro tipo II)	Decisão correta