Capítulo 12 Medidas e instrumentos


12.1 Escalas


12.1.1 O que são escalas?

  • Uma escala de medição grosseira representa um construto de natureza contínua medido por itens tais que diferentes pontuações são agrupadas na mesma categoria no ato da coleta de dados.125

  • Em escalas grosseiras, erros são introduzidos porque as variações contínunas do constructo são colapsadas em uma mesma categorias ou separadas entre categorias próximas.125

  • Escalas tipo Likert com 5 categorias tipo “discordo totalmente”, “discordo parcialmente”, “nem concordo nem discordo”, “concordo parcialmente”, e “concordo totalmente” são escalas grosseira porque as diferenças entre as categorias não são iguais. Por exemplo, a diferença entre “discordo totalmente” e “discordo parcialmente” não é a mesma que a diferença entre “concordo parcialmente” e “concordo totalmente”.125


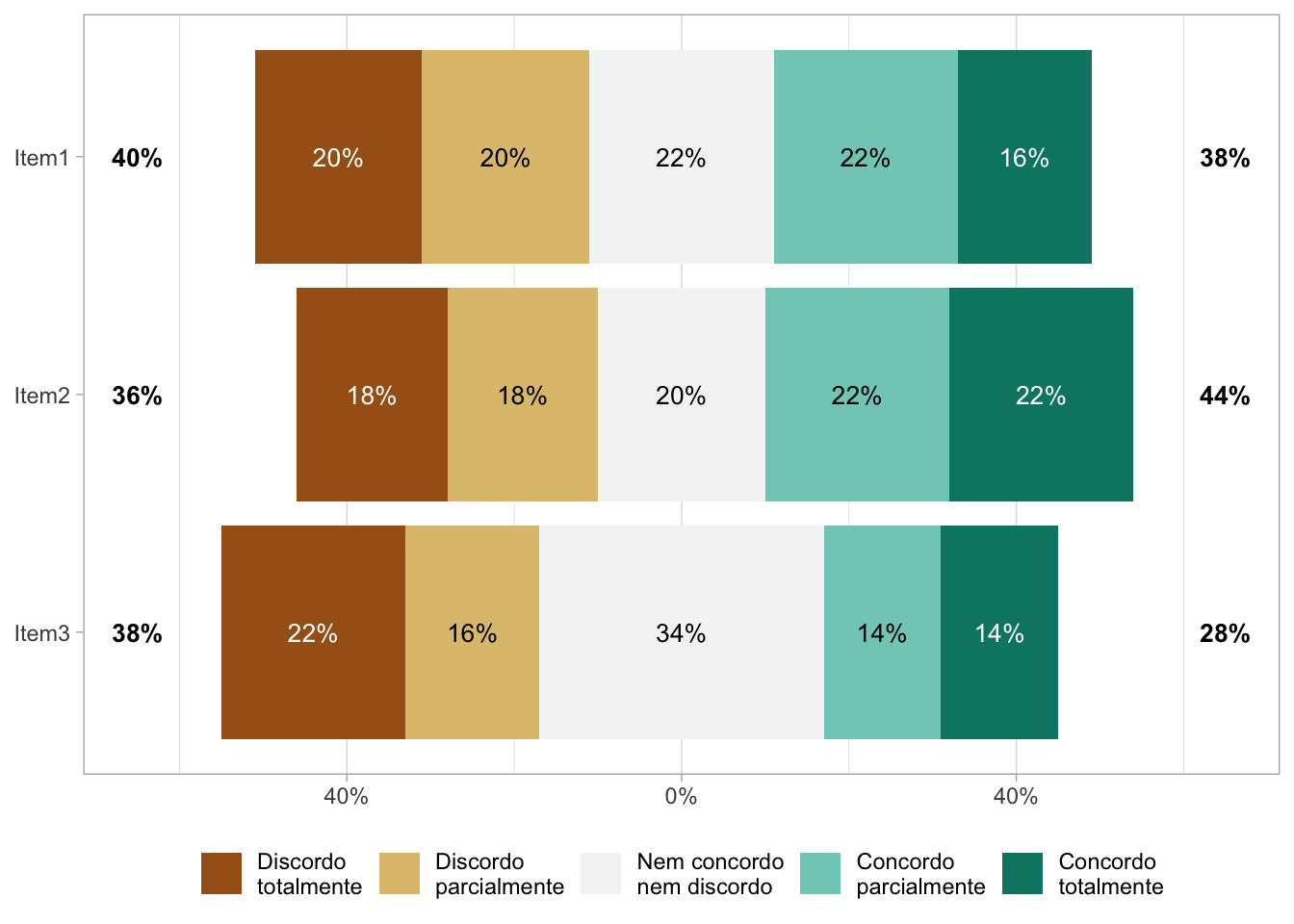
Exemplo de instrumento com 3 itens tipo Likert com 5 categorias cada.

Figura 12.1: Exemplo de instrumento com 3 itens tipo Likert com 5 categorias cada.

Tabela 12.1: Descrição dos itens tipo Likert do instrumento.
Itens Discordância Neutro Concordância Média DP
Item1 40 22 38 2.94 1.38
Item2 36 20 44 3.12 1.42
Item3 38 34 28 2.82 1.32




  • O erros em escalas grosseiras é considerado sistemático mas não pode ser corrigido em nível da unidade de análise.125


12.2 Medição e Medidas


12.2.1 O que é medição?

  • Processo empírico, realizado por meio de um instrumento, que estabelece uma correspondência rigorosa e objetiva entre uma observação e uma categoria em um modelo da observação.140

  • Esse processo tem como objetivo distinguir de maneira substantiva a manifestação observada de outras possíveis manifestações que também possam ser diferenciadas.140


12.2.2 O que são medidas diretas?


12.2.3 O que são medidas derivadas?


12.2.4 O que são medidas por teoria?


12.2.5 O que são medidas únicas?

  • A medida única da pressão arterial sistólica no braço esquerdo resulta em um valor pontual.REF?

  • Medidas únicas obtidas de diferentes unidades de análise podem ser consideradas independentes se observadas outras condições na coleta de dados.REF?

  • O valor pontual será considerado representativo da variável para a unidade de análise (ex.: 120 mmHg para o participante #9).


Tabela 12.2: Dados brutos com medidas únicas.
Unidade de análise Pressão arterial, braço esquerdo (mmHg)
1 118
2 113
3 116
4 110
5 111
6 116
7 120
8 111
9 120
10 112


12.2.6 O que são medidas repetidas?

  • As medidas repetidas podem ser tabuladas separadamente, por exemplo para análise da confiabilidade de obtenção dessa medida.REF?

  • A medida repetida da pressão arterial no braço esquerdo resulta em um conjunto de valores pontuais (ex.: 110 mmHg, 118 mmHg e 116 mmHg para o participante #5).


Tabela 12.3: Dados brutos com medidas repetidas.
Unidade de análise Pressão arterial, braço esquerdo (mmHg) #1 Pressão arterial, braço esquerdo (mmHg) #2 Pressão arterial, braço esquerdo (mmHg) #3
1 114 112 112
2 115 120 113
3 115 110 120
4 117 116 114
5 110 118 116
6 110 120 113
7 118 114 117
8 111 112 119
9 120 112 117
10 110 115 115


  • As medidas repetidas podem ser agregadas por algum parâmetro — ex.: média, mediana, máximo, mínimo, entre outros —, observando-se a relevância biológica, clínica e/ou metodológica desta escolha.REF?

  • Medidas agregadas obtidas de diferentes unidades de análise podem ser consideradas independentes se observadas outras condições na coleta de dados.REF?

  • O valor agregado será considerado representativo da variável para a unidade de análise (ex.: média = 115 mmHg para o participante #5).


Tabela 12.4: Dados brutos com medidas repetidas agregadas.
Unidade de análise Pressão arterial, braço esquerdo (mmHg) média
1 113
2 116
3 115
4 116
5 115
6 114
7 116
8 114
9 116
10 113



12.2.7 O que são medidas seriadas?

  • Medidas seriadas são possivelmente relacionadas e, portanto, dependentes na mesma unidade de análise.REF?

  • Por exemplo, a medida seriada da pressão arterial no braço esquerdo, em intervalos tipicamente regulares (ex.: 114 mmHg, 120 mmHg e 110 mmHg em 1 min, 2 min e 3 min, respectivamente, para o participante #1).


Tabela 12.5: Dados brutos com medidas seriadas não agregadas.
Unidade de análise Tempo (min) Pressão arterial, braço esquerdo (mmHg)
1 1 114
1 2 120
1 3 110
2 1 119
2 2 120
2 3 114
3 1 116
3 2 114
3 3 116
4 1 113


  • Medidas seriadas também agregadas por parâmetros — ex.: máximo, mínimo, amplitude — são consideradas representativas da variação temporal ou de uma característica de interesse (ex.: amplitude = 10 mmHg para o participante #1).


Tabela 12.6: Dados brutos com medidas seriadas não agregadas.
Unidade de análise Pressão arterial, braço esquerdo (mmHg) amplitude
1 10
2 6
3 2
4 6
5 1
6 8
7 9
8 10
9 7
10 5



12.2.8 O que são medidas múltiplas?

  • Medidas múltiplas também são possivelmente relacionadas e, portanto, são dependentes na mesma unidade de análise. Medidas múltiplas podem ser obtidas de modo repetido para análise agregada ou seriada.REF?

  • A medida de pressão arterial bilateral resulta em um conjunto de valores pontuais (ex.: braço esquerdo = 114 mmHg, braço direito = 118 mmHg para o participante #8). Neste caso, ambos os valores pontuais são considerados representativos daquela unidade de análise.


Tabela 12.7: Dados brutos com medidas múltiplas.
Unidade de análise Pressão arterial, braço esquerdo (mmHg) Pressão arterial, braço direito (mmHg)
1 117 115
2 120 118
3 112 118
4 112 112
5 116 112
6 112 118
7 115 113
8 114 118
9 119 114
10 112 116



12.3 Erro de medida


12.3.1 O que são erros de medida?

  • A natureza dos erros de medida são em geral atribuídos aos (1) instrumentos utilizados e variações no protocolo, na medida em que o seu tamanho médio pode ser reduzido por modificações e melhorias nesses instrumentos; e (2) variações genuínas medida em de curto prazo.142

  • Estimativa pontual (um número exato) é um evento de probabilidade 0 sob um modelo contínuo.REF?

  • Precisão como faixa \(±\epsilon\) tem probabilidade > 0, mensurável e dependente de \(\sigma\).REF?

  • Isso motiva trabalhar com intervalos (faixas) em vez de pontos.REF?


Ilustração do conceito de erro de medida em um modelo simples com erro normal. A linha tracejada indica o valor verdadeiro (desconhecido na prática). A área sombreada representa a probabilidade de cair na faixa |X - θ| ≤ ε, que é > 0. A probabilidade de 'acertar no ponto' X = θ é 0 (linha tracejada).

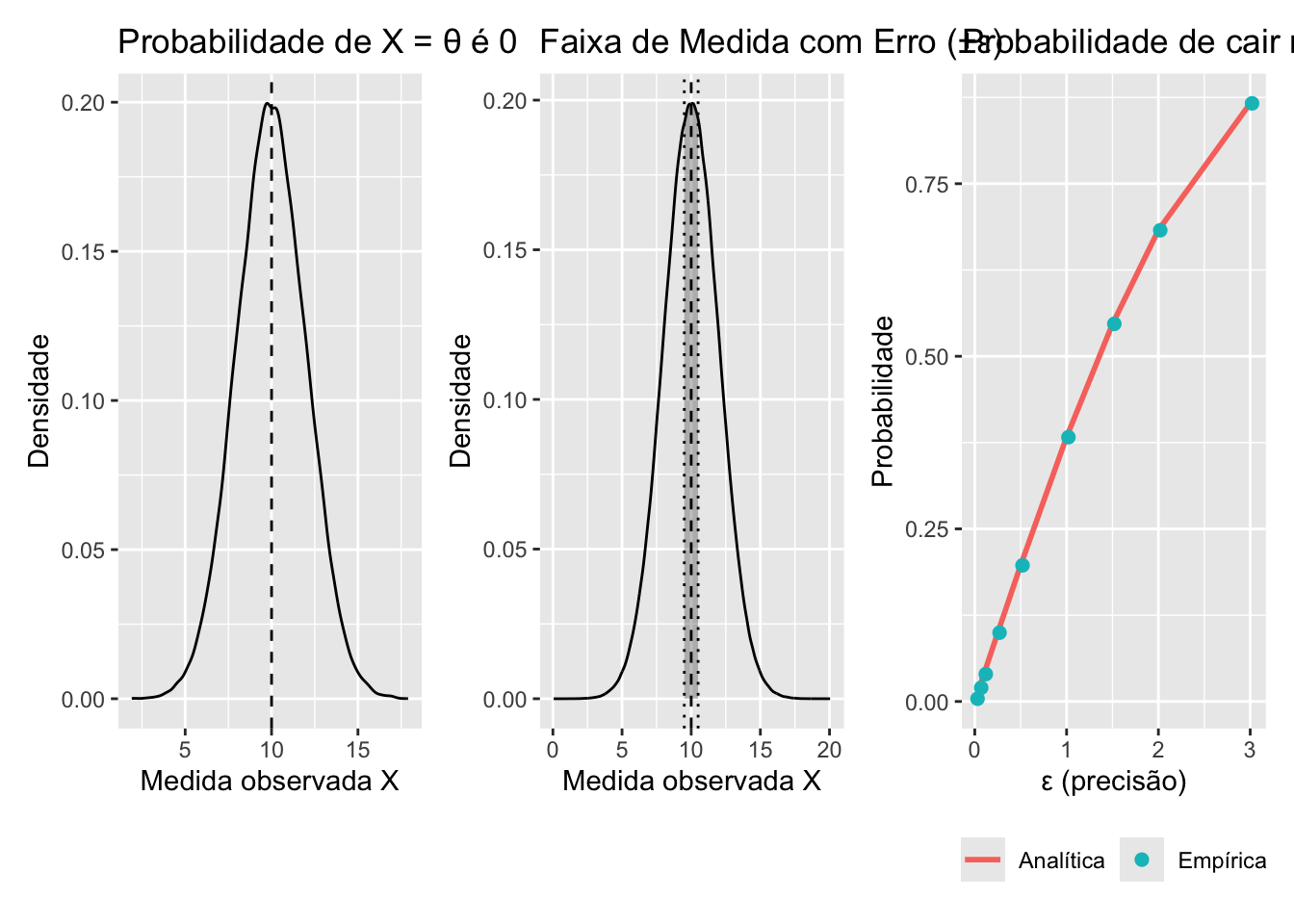
Figura 12.2: Ilustração do conceito de erro de medida em um modelo simples com erro normal. A linha tracejada indica o valor verdadeiro (desconhecido na prática). A área sombreada representa a probabilidade de cair na faixa |X - θ| ≤ ε, que é > 0. A probabilidade de ‘acertar no ponto’ X = θ é 0 (linha tracejada).


12.3.2 Quais fontes de variabilidade são comumente investigadas?

  • Intra/Entre participantes (isto é, unidades de análise).143

  • Intra/Entre repetições.143

  • Intra/Entre observadores.143


12.4 Instrumentos


12.4.1 O que são instrumentos?


12.5 Acurácia e precisão


12.5.1 O que é acurácia?

  • Acurácia expressa a proximidade de concordância entre uma mensuração e o valor real.144

  • Acurária está para medidas como validade está para instrumentos de medida.REF?


12.5.2 O que é precisão?

  • Precisão se refere à proximidade de concordância entre resultados de testes independentes obtidos nas mesmas condições de teste.144

  • Precisão é um índice de quão próximo os resultados podem ser repetidos entre mensurações repetidas.145

  • Precisão está para medidas como confiabilidade está para instrumentos de medida.REF?


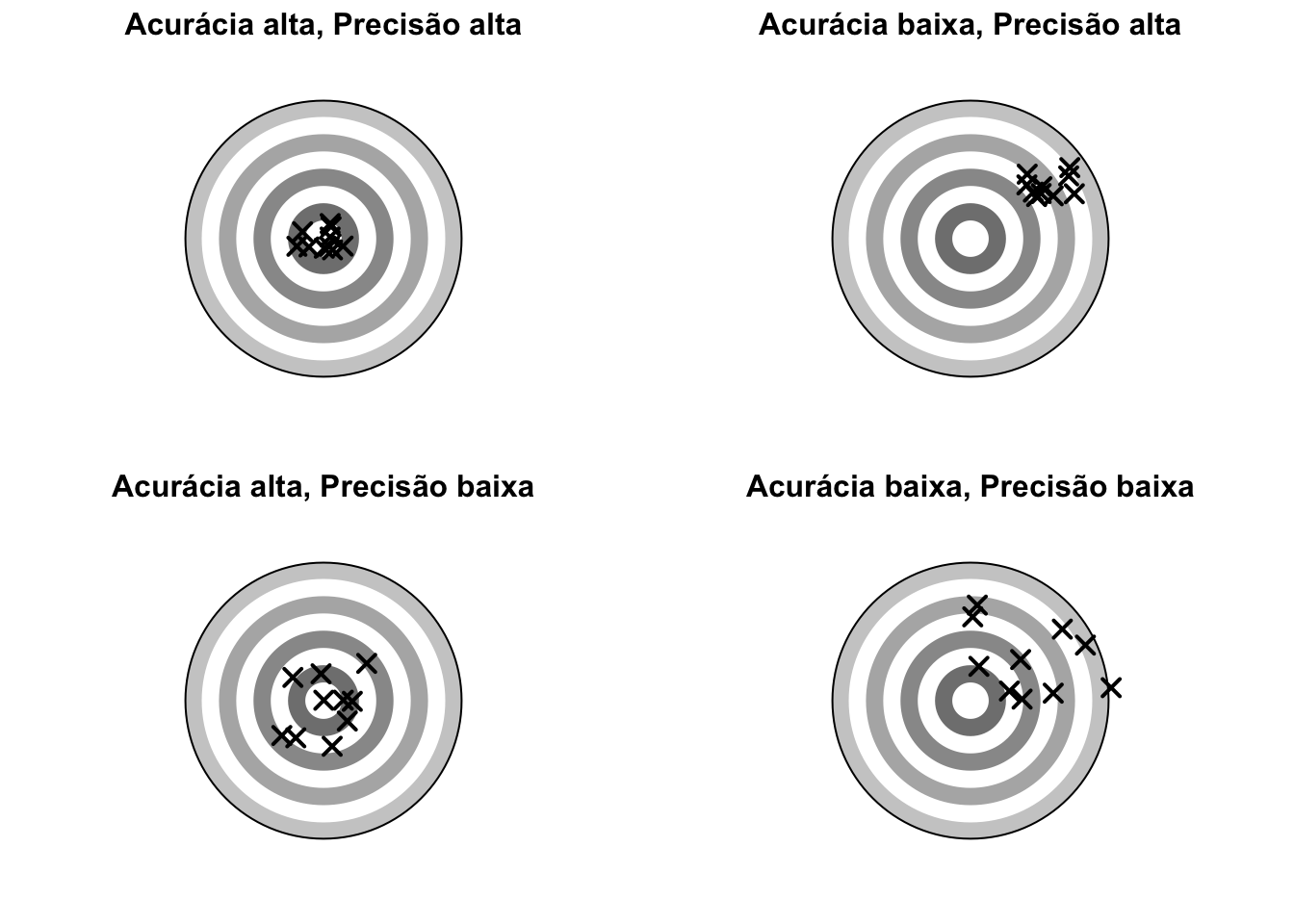
Acurácia e precisão como propriedades de uma medida.

Figura 12.3: Acurácia e precisão como propriedades de uma medida.


12.6 Viés e variabilidade


12.6.1 Qual é a relação entre viés e variabilidade?


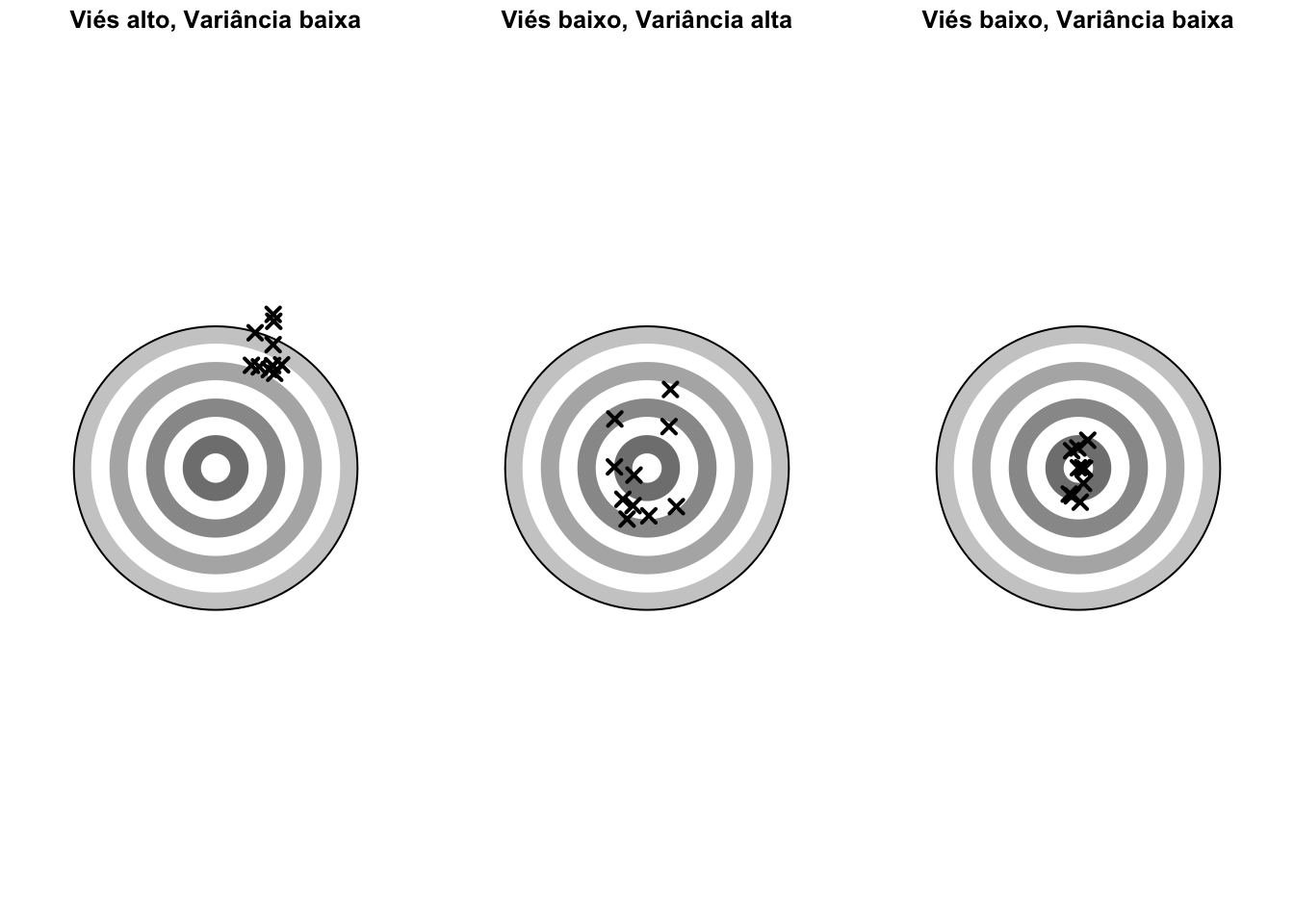
Viés e variabilidade de uma medida.

Figura 12.4: Viés e variabilidade de uma medida.



Citar como:
Ferreira, Arthur de Sá. Ciência com R: Perguntas e respostas para pesquisadores e analistas de dados. Rio de Janeiro: 1a edição,


Referências

125.
Aguinis H, Pierce CA, Culpepper SA. Scale Coarseness as a Methodological Artifact. Organizational Research Methods. 2008;12(4):623–652. doi:10.1177/1094428108318065
138.
Bryer J, Speerschneider K. likert: Analysis and Visualization Likert Items.; 2016. https://CRAN.R-project.org/package=likert.
139.
Larmarange J. ggstats: Extension to ggplot2 for Plotting Stats.; 2025. doi:10.32614/CRAN.package.ggstats
140.
Ferris TLJ. A new definition of measurement. Measurement. 2004;36(1):101–109. doi:10.1016/j.measurement.2004.03.001
141.
R Core Team. R: A Language and Environment for Statistical Computing.; 2023. https://www.R-project.org/.
142.
Healy MJR, Goldstein H. Regression to the mean. Annals of Human Biology. 1978;5(3):277–280. doi:10.1080/03014467800002891
143.
Altman DG, Bland JM. Measurement in Medicine: The Analysis of Method Comparison Studies. The Statistician. 1983;32(3):307. doi:10.2307/2987937
144.
Menditto A, Patriarca M, Magnusson B. Understanding the meaning of accuracy, trueness and precision. Accreditation and Quality Assurance. 2006;12(1):45–47. doi:10.1007/s00769-006-0191-z
145.
Streiner DL, Norman GR. “Precision” and “Accuracy”: Two Terms That Are Neither. Journal of Clinical Epidemiology. 2006;59(4):327–330. doi:10.1016/j.jclinepi.2005.09.005