Capítulo 53 Meta-análise

53.1 Características

53.1.1 O que é meta-análise?

• Meta-análise é um método estatístico que combina quantitativamente os resultados de múltiplos estudos independentes sobre uma mesma questão de pesquisa, aumentando o poder estatístico e a precisão das estimativas de efeito.⁴²⁶

• Meta-análise sintetiza evidências considerando o peso de cada estudo (geralmente inversamente proporcional à variância) e permite avaliar a consistência dos resultados, identificar fontes de heterogeneidade e estimar um efeito global.⁴²⁶

53.2 Modelos de meta-análise

53.2.1 Quais são os principais modelos de meta-análise?

• Modelo de efeitos fixos: assume que todos os estudos avaliam o mesmo efeito verdadeiro, e a variação observada é apenas devido ao erro de amostragem. É adequado quando os estudos são homogêneos e as diferenças entre eles são pequenas.⁴²⁶

• Modelo de efeitos aleatórios: assume que os estudos avaliam efeitos verdadeiros diferentes, com uma distribuição normal. É mais apropriado quando há heterogeneidade entre os estudos, pois considera a variação entre eles além do erro de amostragem.⁴²⁶

• Modelo de efeitos de rede: estende a meta-análise para comparar múltiplas intervenções simultaneamente, mesmo que não tenham sido comparadas diretamente em estudos. É útil para avaliar a eficácia relativa de várias intervenções.^REF?

O pacote metafor⁴²⁷ fornece a função forest para criar figuras tipo forest plot.

O pacote netmeta⁴²⁸ fornece a função netmeta para realizar meta-análise de rede usando método de grafo.

O pacote gemtc⁴²⁹ fornece a função mtc.model para criar modelos de meta-análise de rede.

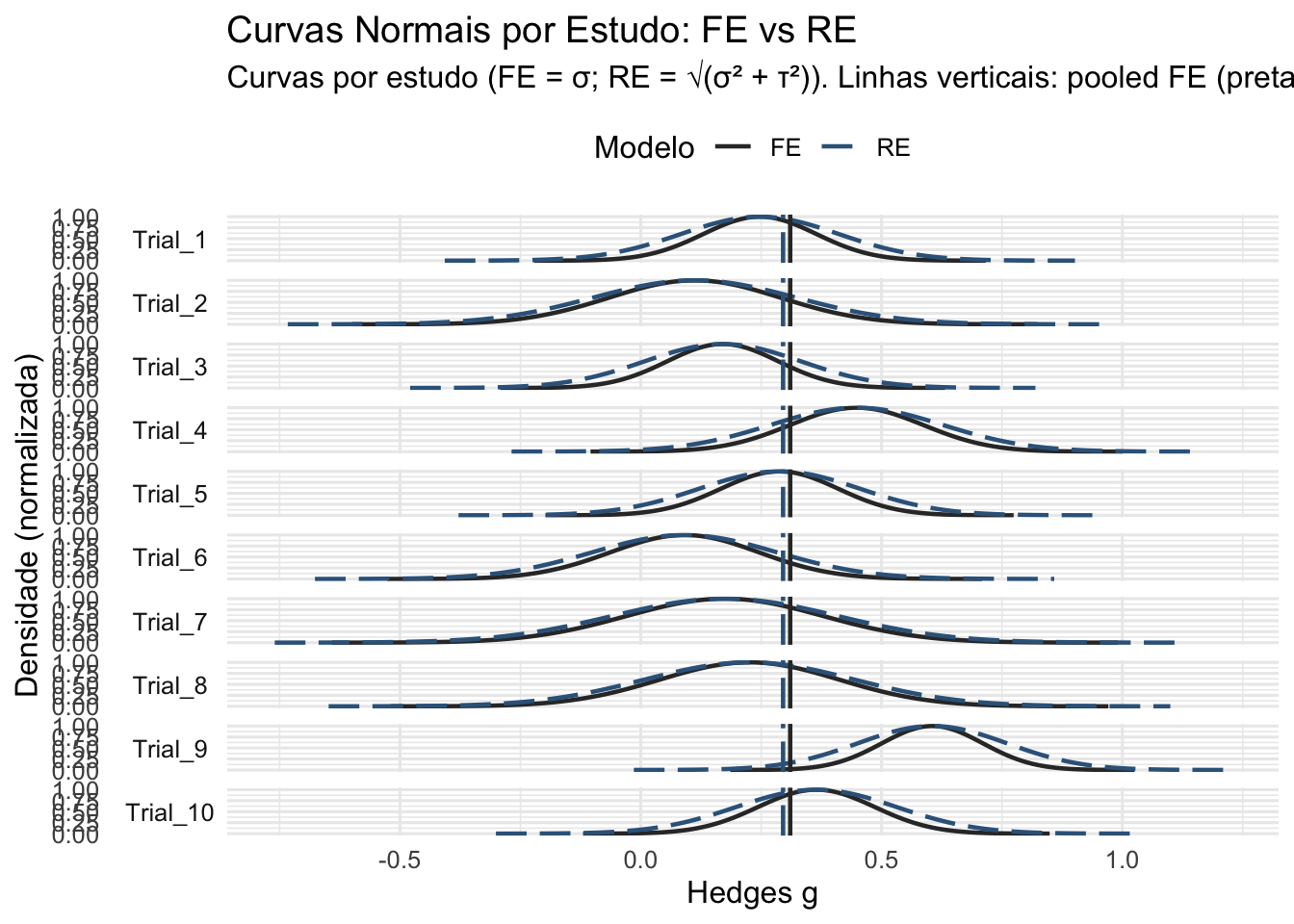
Figura 53.1: Comparação entre modelos de efeito fixo e aleatório com 10 ensaios clínicos simulados.

53.3 Conversão de Medidas em Meta-análises

53.3.1 O que fazer quando os estudos apresentam resultados com diferentes parâmetros?

• Quando os estudos reportam médias e desvios-padrão, os dados podem ser usados diretamente na metanálise.^REF?

• Quando apresentam mediana e intervalo interquartil (ou mínimo–máximo), existem métodos estatísticos para converter em média e DP.⁴³⁰

• Hozo et al. (2005) propuseram fórmulas para estimar a média e o desvio-padrão a partir da mediana, amplitude e tamanho da amostra.⁴³⁰

• Wan et al. (2014) aperfeiçoaram essas estimativas, oferecendo métodos mais precisos para converter mediana e IQR em média e DP.⁴³¹

O pacote metafor⁴²⁷ fornece a função conv.fivenum para converter mínimo/mediana/máximo ou Q1/mediana/Q2 em média e desvio-padrão.

53.4 Interpretação de efeitos em meta-análise

53.4.1 Como avaliar a variação do tamanho do efeito?

• O intervalo de predição contém informação sobre a variação do tamanho do efeito.⁴³²

• Se o intervalo de predição não contém a hipótese nula (\(H_{0}\)), podemos concluir que (a) o tratamento funciona igualmente bem em todas as populações, ou que ele funciona melhor em algumas populações do que em outras.⁴³²

• Se o intervalo de predição contém a hipótese nula (\(H_{0}\)), podemos concluir que o tratamento pode ser benéfico em algumas populações, mas prejudicial em outras, de modo que a estimativa pontual (geralmente a média) torna-se amplamente irrelevante. Nesse caso, é recomendado investigar em que populações o tratamento seria benéfico e em quais causaria danos.⁴³²

53.4.2 Como avaliar a heterogeneidade entre os estudos?

• A heterogeneidade — variação não-aleatória — no efeito do tratamento entre os estudos incluídos em uma meta-análise pode ser avaliada pelo \(I^{2}\) (53.1).^432,433

\[\begin{equation} \tag{53.1} I^{2} = \max \left( 0, \frac{Q - df}{Q} \right) \times 100\% \end{equation}\]

• \(I^{2}\) representa qual proporção da variância observada reflete a variância nos efeitos verdadeiros em vez do erro de amostragem.⁴³²

• \(I^{2}\) mede a proporção da variância total que pode ser atribuída à heterogeneidade entre os estudos incluídos.⁴³³

• \(I^{2}\) não depende da quantidade de estudos incluídos na meta-análise. Entretanto, \(I^{2}\) aumenta com a quantidade de participantes incluídos nos estudos meta-analisados.⁴³³

• A heterogeneidade entre estudos é explicada de modo mais confiável utilizando dados de pacientes individuais, uma vez que a direção verdadeira da modificação de efeito não pode ser observada a partir de dados agregados no estudo.⁴³⁴

O pacote psychmeta³⁰⁰ fornece a função ma_d para meta-analisar valores d.

O pacote psychmeta³⁰⁰ fornece a função ma_r para meta-analisar correlações.

53.5 Interpretação do forest plot

53.5.1 O que é um forest plot?

• Um forest plot é uma representação gráfica dos achados de uma meta-análise. Ele resume os resultados de estudos individuais e apresenta uma estimativa combinada do efeito, permitindo interpretação visual da magnitude, direção e significância estatística dos resultados.⁴³⁵

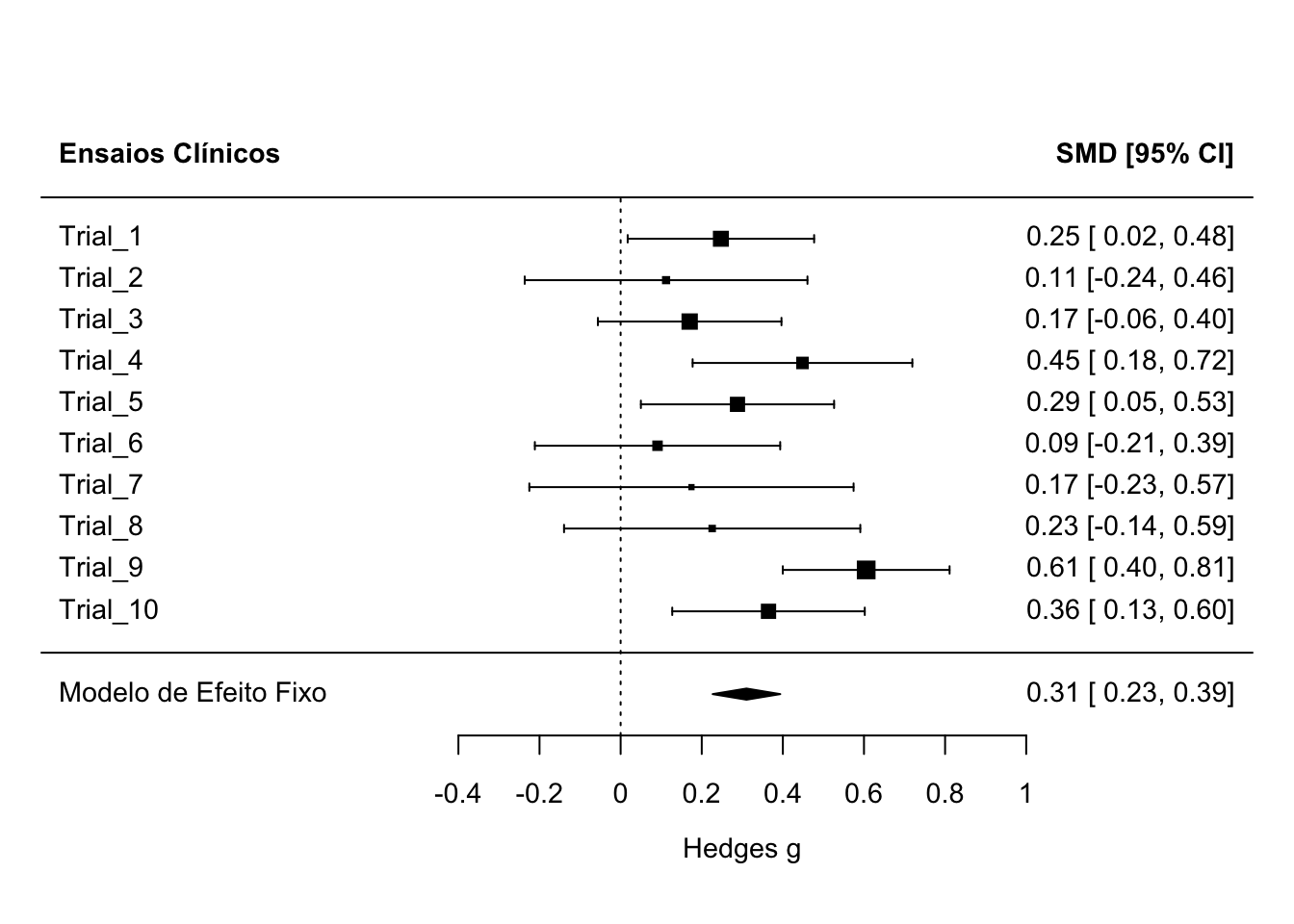
Figura 53.2: Forest plot de uma meta-análise de efeito fixo com 10 ensaios clínicos simulados.

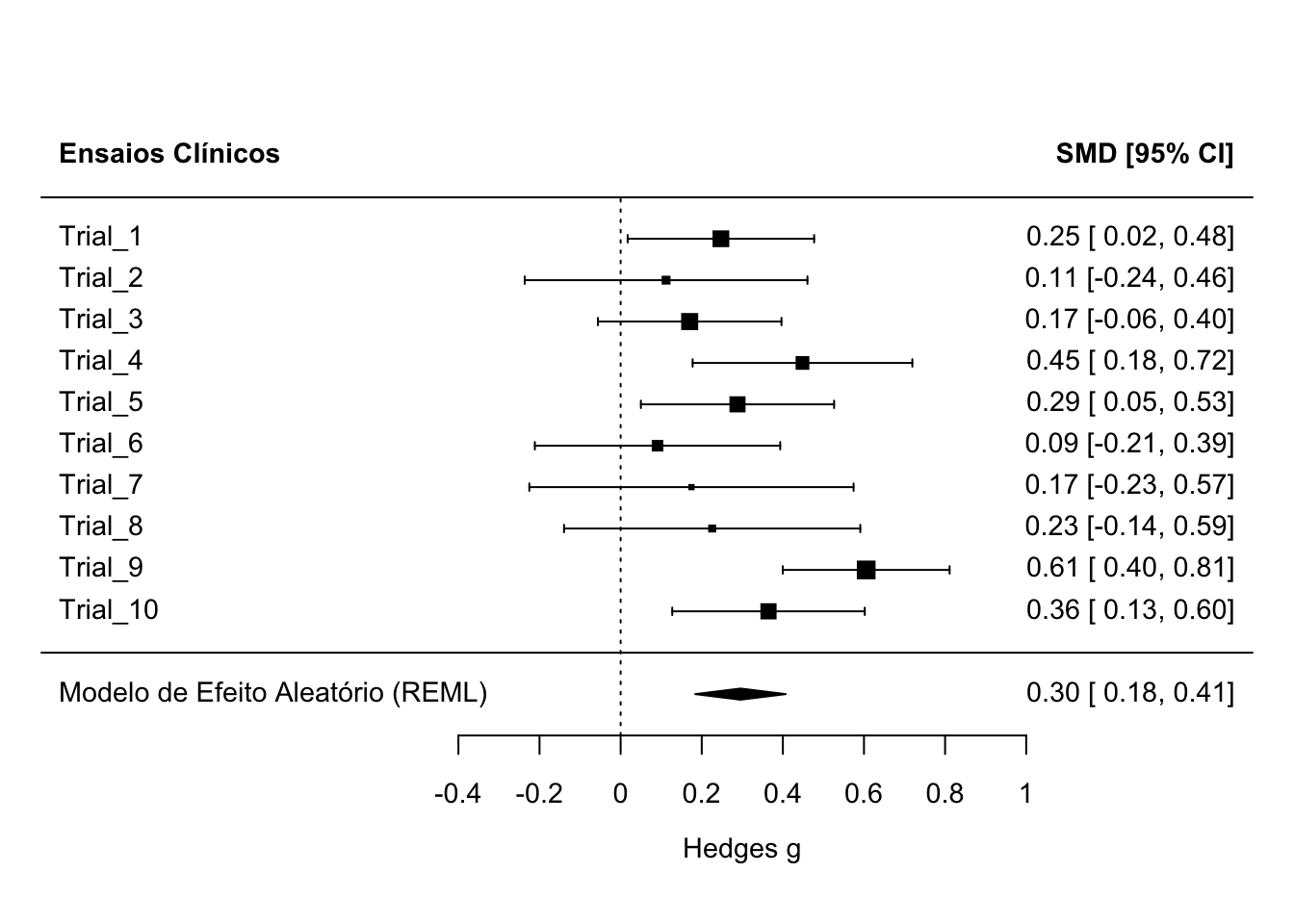
Figura 53.3: Forest plot de uma meta-análise de efeito aleatório com 10 ensaios clínicos simulados.

53.5.2 Quais são as seis colunas básicas que um forest plot geralmente apresenta?

• As seis colunas básicas incluem: estudos incluídos (e subgrupos, se analisados); dados do grupo de intervenção, dados do grupo controle; peso de cada estudo; medida numérica do efeito; representação gráfica do efeito.⁴³⁵

53.5.3 Como diferenciar um desfecho binário de um contínuo em um forest plot?

• Em desfechos binários, são mostrados número de eventos e total da amostra, sendo o efeito medido por risk ratio (\(RR\)) ou odds ratio (\(OR\)).⁴³⁵

• Em desfechos contínuos, apresentam-se médias, desvios-padrão e tamanhos amostrais, com o efeito medido pela diferença de médias.⁴³⁵

53.5.4 O que representa o ponto central da caixa e o tamanho desta no gráfico?

• O ponto central indica a estimativa pontual do efeito (melhor estmativa para o efeito real).⁴³⁵

• O tamanho da caixa é proporcional ao peso do estudo na meta-análise, geralmente maior para estudos com amostras maiores.⁴³⁵

53.5.5 Qual é o significado da linha vertical do “nenhum efeito”?

• É a linha de referência que indica efeito nulo.⁴³⁵

• Para desfechos binários, corresponde ao valor 1 (\(RR\) ou \(OR\) = 1).⁴³⁵

• Para desfechos contínuos, corresponde ao valor 0 (diferença de médias = 0).⁴³⁵

• Se o intervalo de confiança de um estudo ou do resultado combinado cruza essa linha, o resultado não é estatisticamente significativo.⁴³⁵

53.5.6 Como interpretar o diamante na parte inferior do forest plot?

• O diamante representa o efeito combinado dos estudos incluídos.⁴³⁵

• O ponto central do diamante é a estimativa global.⁴³⁵

• A largura do diamante representa o intervalo de confiança de 95% para o efeito combinado.⁴³⁵

53.5.7 Como a heterogeneidade pode ser avaliada no forest plot?

• A variabilidade nos resultados dos estudos incluídos é avaliada pela sobreposição dos intervalos de confiança dos estudos; pelo teste do qui-quadrado (\(\chi^2\)) e pelo valor de \(I^{2}\).⁴³⁵

53.5.8 Quais são as interpretações usuais para os valores de \(I^{2}\)?

• 0% a 40%: pode não ser importante; 30% a 60%: heterogeneidade moderada; 50% a 90%: heterogeneidade substancial; 75% a 100%: heterogeneidade considerável.⁴³⁵

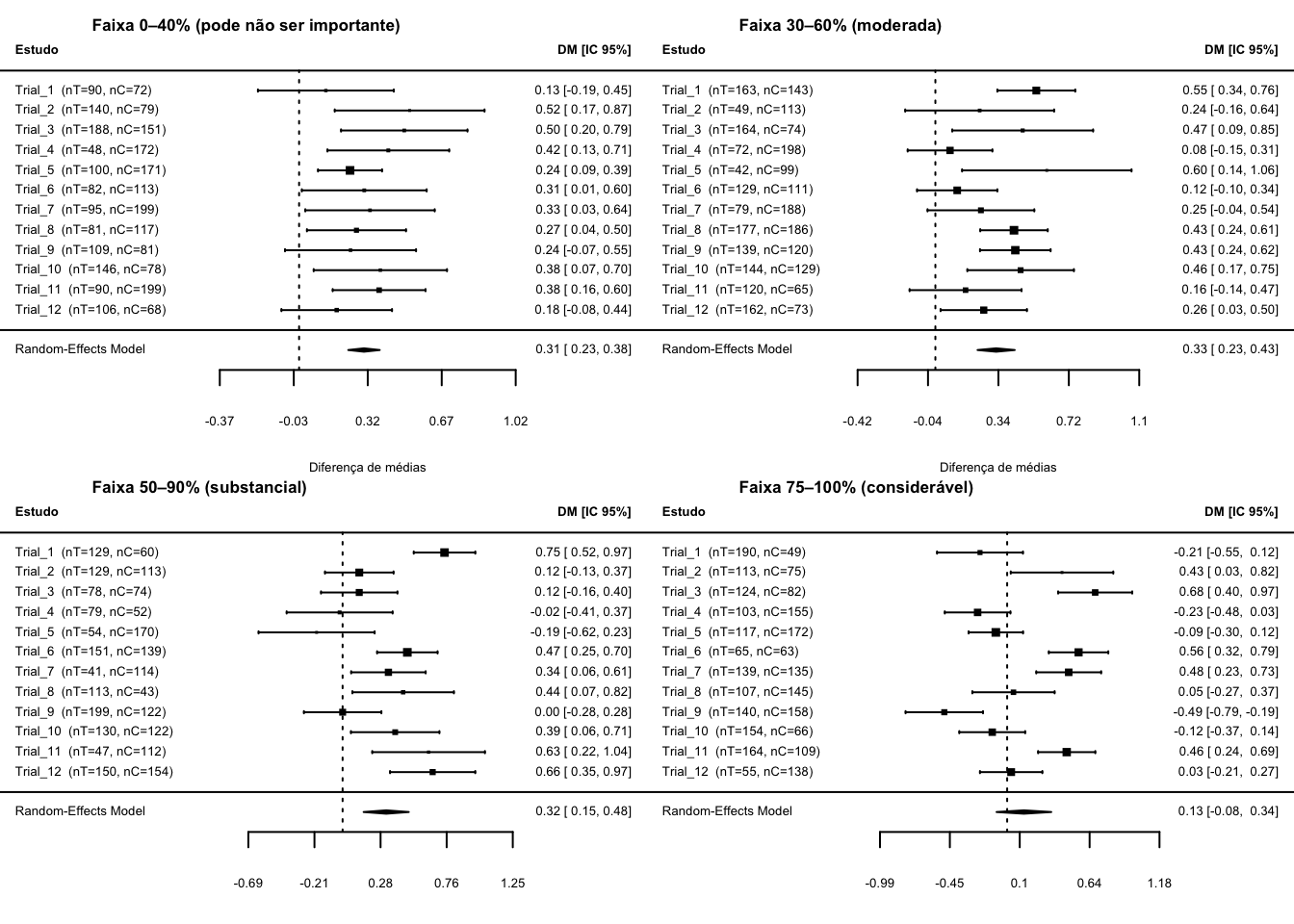
Figura 53.4: Forest plots ilustrativos para faixas usuais de \(I^2\).

53.6 Viés de publicação em meta-análises

53.6.1 O que é viés de publicação?

• O viés de publicação ocorre quando estudos com resultados não significativos ou contrários à hipótese tendem a não ser publicados, afetando a estimativa final da meta-análise e podendo levar a conclusões incorretas.⁴³⁶

53.6.2 Quais métodos podem ser usados para identificar viés de publicação?

• O método mais simples é o funnel plot, que representa a estimativa de efeito de cada estudo em função de sua precisão (\(1/SE\)).⁴³⁷

• Na ausência de viés, espera-se uma distribuição simétrica (“forma de funil”). Assimetria pode indicar viés de publicação, heterogeneidade entre estudos ou efeitos de tamanho de estudo (small-study effects).⁴³⁷

• Para odds ratios (\(OR\)), a correlação entre \(ln(OR)\) e seu erro padrão pode gerar assimetria mesmo sem viés, por isso recomenda-se, nesses casos, plotar em função do tamanho amostral.⁴³⁸

53.6.3 O que é um gráfico de funil (funnel plot)?

• É um gráfico de dispersão que relaciona a estimativa de efeito de cada estudo com uma medida de seu tamanho ou precisão (por exemplo, erro-padrão no eixo vertical, em escala invertida). Em condições ideais (ausência de viés e heterogeneidade), os estudos se distribuem de forma simétrica, formando um “funil invertido”.⁴³⁹

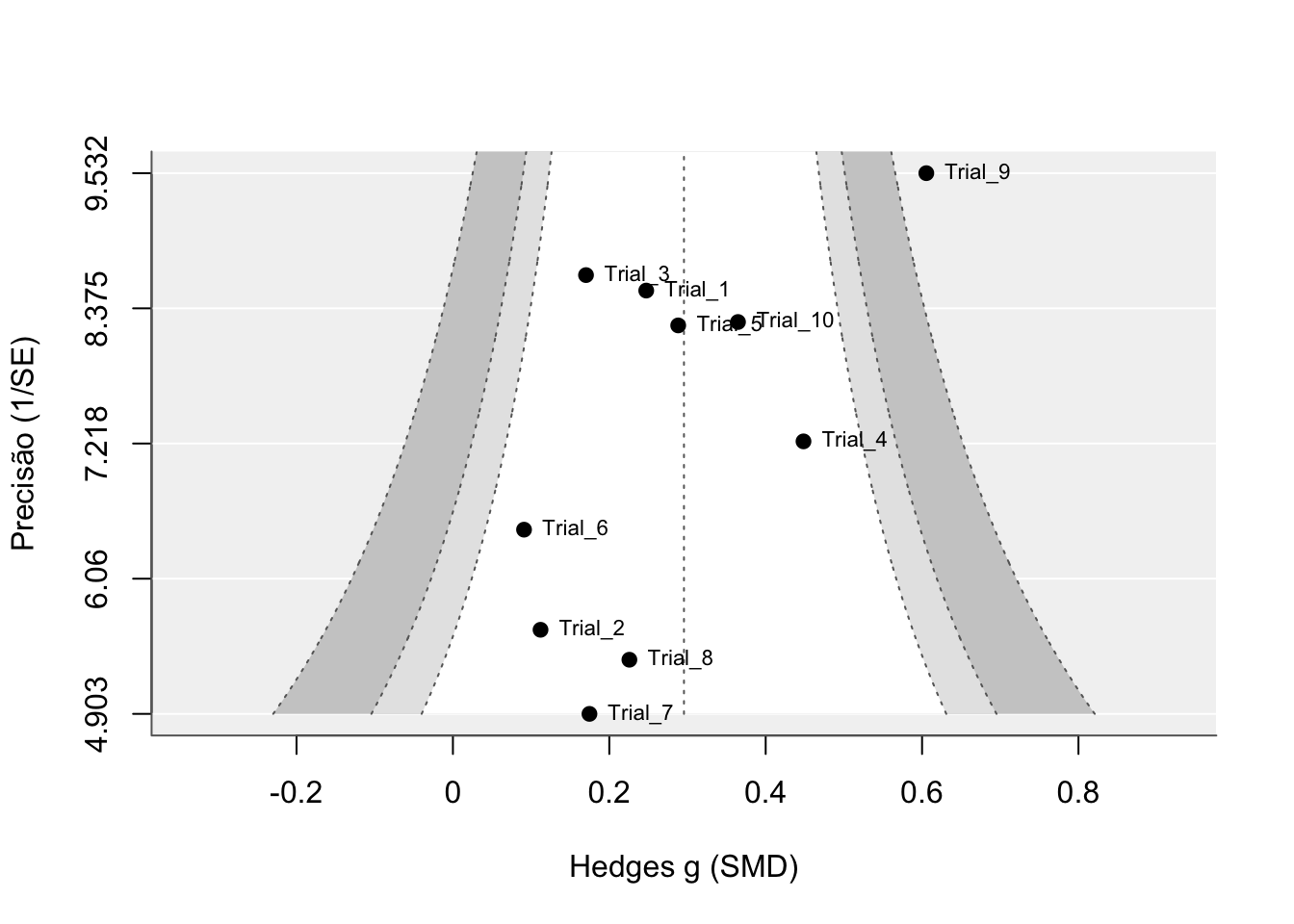
Figura 53.5: Gráficos de funil simulados com baixa e alta heterogeneidade.

53.6.4 A assimetria do funnel plot indica sempre viés de publicação?

• Viéses de relato (reporting biases), como viés de publicação, viés de linguagem ou de citação.⁴³⁹

• Diferenças metodológicas entre estudos pequenos e grandes.⁴³⁹

• Heterogeneidade verdadeira (diferença real no efeito conforme o tamanho ou o contexto do estudo).⁴³⁹

• Artefatos estatísticos ou mero acaso.⁴³⁹

53.6.5 O que é trim and fill?

• O método trim and fill “apara” (trim) os estudos que causam assimetria no funnel plot, estima o número de estudos possivelmente ausentes (não publicados) e “preenche” (fill) o gráfico com esses estudos simulados, recalculando o efeito combinado.⁴⁴⁰

• O método assume que a assimetria é causada unicamente por viés de publicação, podendo levar a conclusões equivocadas quando há outras causas, como heterogeneidade.⁴⁴⁰

53.6.6 O que é o teste de Egger?

• É um teste estatístico amplamente utilizado que avalia a relação entre o efeito padronizado (\(efeito/SE\)) e a precisão (\(1/SE\)).⁴³⁷

• No entanto, para meta-análises com \(OR\), apresenta taxas de erro tipo I excessivas, especialmente quando o efeito é grande ou há alta heterogeneidade.⁴³⁸

53.6.7 O que é o teste de Peters?

• Uma regressão linear ponderada com \(ln(OR)\) como variável dependente e o inverso do tamanho total da amostra como variável independente (modificação do teste de Macaskill).⁴³⁸

• Essa abordagem reduz a correlação entre \(ln(OR)\) e seu \(SE\), resultando em taxas de erro tipo I mais adequadas (~10%) independentemente do tamanho do efeito, número de estudos ou heterogeneidade.⁴³⁸

• O teste de Peters é preferível ao teste de Egger quando o desfecho é expresso como OR, pois mantém taxas de erro tipo I adequadas e ainda apresenta poder comparável para detectar viés em condições de baixa heterogeneidade.⁴³⁸

• Em casos de alta heterogeneidade, o teste de Egger pode apresentar maior poder, mas sua alta taxa de falsos positivos compromete a interpretação.⁴³⁸

53.6.8 Quais são as recomendações para testar a assimetria?

• Evitar testes quando há menos de 10 estudos, devido ao baixo poder estatístico.⁴³⁹

• Inspecionar visualmente o funnel plot junto com os resultados dos testes.⁴³⁹

• Para desfechos contínuos (diferença de médias), o teste de Egger pode ser usado.⁴³⁹

• Para desfechos dicotômicos expressos como odds ratio (\(OR\)) com baixa heterogeneidade (\(\tau^2 < 0,1\)), considerar os testes de Harbord, Peters ou Rücker.⁴³⁹

• Para desfechos dicotômicos expressos como odds ratio(\(OR\)) com alta heterogeneidade (\(\tau^2 > 0,1\)), o teste de Rücker com transformação \(arcsine\) é mais indicado.⁴³⁹

53.6.9 Como interpretar os resultados de testes de viés de publicação?

• Um resultado não significativo não garante ausência de viés.⁴³⁸

• Recomenda-se complementar com inspeção visual do funnel plot e considerar métodos adicionais como trim and fill.^438,440

• Quando há suspeita de viés, discutir as implicações e interpretar o efeito combinado com cautela.⁴³⁸

O pacote psychmeta³⁰⁰ fornece a função plot_funnel para criar figuras tipo funnel plot.

53.7 Diretrizes para redação

53.7.1 Quais são as diretrizes para redação de meta-análises?

• Visite a rede Enhancing the QUAlity and Transparency Of health Research (EQUATOR Network) para encontrar diretrizes específicas.

• The PRISMA 2020 statement: An updated guideline for reporting systematic reviews:⁴⁴¹ https://www.equator-network.org/reporting-guidelines/prisma/

• Transparent reporting of multivariable prediction models for individual prognosis or diagnosis: checklist for systematic reviews and meta-analyses (TRIPOD-SRMA).⁴²⁴ https://www.equator-network.org/reporting-guidelines/tripod-srma/

O pacote metagear⁴⁴² fornece a função plot_PRISMA para gerar o fluxograma de uma revisão sistemática de acordo com o Preferred Reporting Items for Systematic Reviews and Meta-Analyses⁴⁴³.

O pacote PRISMA2020⁴⁴⁴ fornece a função PRISMA_flowdiagram para elaboração do fluxograma de revisões sistemáticas no formato padrão.

Citar como:
Ferreira, Arthur de Sá. Ciência com R: Perguntas e respostas para pesquisadores e analistas de dados. Rio de Janeiro: 1a edição,

Referências

300.

Dahlke JA, Wiernik BM. psychmeta: An R Package for Psychometric Meta-Analysis. Applied Psychological Measurement. 2018;43(3):415–416. doi:10.1177/0146621618795933

424.

Snell KIE, Levis B, Damen JAA, et al. Transparent reporting of multivariable prediction models for individual prognosis or diagnosis: checklist for systematic reviews and meta-analyses (TRIPOD-SRMA). BMJ. maio 2023:e073538. doi:10.1136/bmj-2022-073538

426.

Borenstein M, Hedges LV, Higgins JPT, Rothstein HR. A basic introduction to fixed-effect and random-effects models for meta-analysis. Research Synthesis Methods. 2010;1(2):97–111. doi:10.1002/jrsm.12

427.

Viechtbauer W. Conducting meta-analyses in R with the metafor package. Vol 36.; 2010. doi:10.18637/jss.v036.i03

428.

Balduzzi S, Rücker G, Nikolakopoulou A, et al. netmeta: An R Package for Network Meta-Analysis Using Frequentist Methods. Journal of Statistical Software. 2023;106(2):1–40. doi:10.18637/jss.v106.i02

429.

Valkenhoef G van, Kuiper J. gemtc: Network Meta-Analysis Using Bayesian Methods.; 2025. doi:10.32614/CRAN.package.gemtc

430.

Hozo SP, Djulbegovic B, Hozo I. Estimating the mean and variance from the median, range, and the size of a sample. BMC Medical Research Methodology. 2005;5(1). doi:10.1186/1471-2288-5-13

431.

Wan X, Wang W, Liu J, Tong T. Estimating the sample mean and standard deviation from the sample size, median, range and/or interquartile range. BMC Medical Research Methodology. 2014;14(1). doi:10.1186/1471-2288-14-135

432.

Borenstein M. In a meta-analysis, the I-squared statistic does not tell us how much the effect size varies. Journal of Clinical Epidemiology. outubro 2022. doi:10.1016/j.jclinepi.2022.10.003

434.

Grooth HJ de, Parienti JJ. Heterogeneity between studies can be explained more reliably with individual patient data. Intensive Care Medicine. julho 2023. doi:10.1007/s00134-023-07163-z

435.

Dettori JR, Norvell DC, Chapman JR. Seeing the Forest by Looking at the Trees: How to Interpret a Meta-Analysis Forest Plot. Global Spine Journal. 2021;11(4):614–616. doi:10.1177/21925682211003889

436.

Song, Eastwood, Gilbody, Duley, Sutton. Publication and related biases. Health Technology Assessment. 2000;4(10). doi:10.3310/hta4100

437.

Egger M, Smith GD, Schneider M, Minder C. Bias in meta-analysis detected by a simple, graphical test. BMJ. 1997;315(7109):629–634. doi:10.1136/bmj.315.7109.629

438.

Peters JL. Comparison of Two Methods to Detect Publication Bias in Meta-analysis. JAMA. 2006;295(6):676. doi:10.1001/jama.295.6.676

439.

Sterne JAC, Sutton AJ, Ioannidis JPA, et al. Recommendations for examining and interpreting funnel plot asymmetry in meta-analyses of randomised controlled trials. BMJ. 2011;343(jul22 1):d4002–d4002. doi:10.1136/bmj.d4002

440.

Duval S, Tweedie R. Trim and Fill: A Simple Funnel-PlotBased Method of Testing and Adjusting for Publication Bias in Meta-Analysis. Biometrics. 2000;56(2):455–463. doi:10.1111/j.0006-341x.2000.00455.x

441.

Page MJ, McKenzie JE, Bossuyt PM, et al. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. PLOS Medicine. 2021;18(3):e1003583. doi:10.1371/journal.pmed.1003583

442.

Lajeunesse MJ. Facilitating systematic reviews, data extraction, and meta-analysis with the metagear package for R. Methods in Ecology and Evolution. 2016;7(3):323–330. doi:10.1111/2041-210X.12472

443.

Moher D, Shamseer L, Clarke M, et al. Preferred reporting items for systematic review and meta-analysis protocols (PRISMA-P) 2015 statement. Systematic Reviews. 2015;4(1). doi:10.1186/2046-4053-4-1

444.

Haddaway NR, Page MJ, Pritchard CC, McGuinness LA. PRISMA2020: An R package and Shiny app for producing PRISMA 2020-compliant flow diagrams, with interactivity for optimised digital transparency and Open Synthesis. Campbell Systematic Reviews. 2022;18:e1230. doi:10.1002/cl2.1230