Capítulo 36 Modelos

36.1 Modelos

36.1.1 O que são modelos?

Modelos são representações simplificadas de um sistema real, usados para entender, prever ou controlar fenômenos complexos.^REF?

36.1.2 O que é modelagem?

Modelagem é o processo de usar dados para selecionar um modelo matemático explícito que represente o processo gerador dos dados.²⁵⁵

36.1.3 Por que a escolha do modelo é complexa?

Há inúmeras combinações possíveis de variáveis, formas funcionais (lineares, quadráticas, transformações), interações e formas do desfecho, o que torna o espaço de possibilidades muito amplo.²⁵⁵
Todos os modelos são errados, mas alguns são úteis.³²⁵

O pacote equatiomatic³²⁶ fornece a função extract_eq para extrair a equação dos modelos em formato LaTeX para visualização.

36.1.4 O que diferencia modelos clássicos e modernos em predição?

Modelos clássicos, como a regressão logística e as árvores de decisão, contrastam com os modelos modernos, como máquinas de vetor de suporte, redes neurais e random forests , principalmente pela maior flexibilidade e capacidade destes últimos de capturar não linearidades e interações.³²⁷

36.2 Modelos estocásticos

36.2.1 O que são modelos estocásticos?

.^REF?

36.2.2 O que são cadeias de Markov?

As cadeias de Markov descrevem processos em que o estado futuro depende apenas do estado presente, e não da trajetória passada.³²⁸

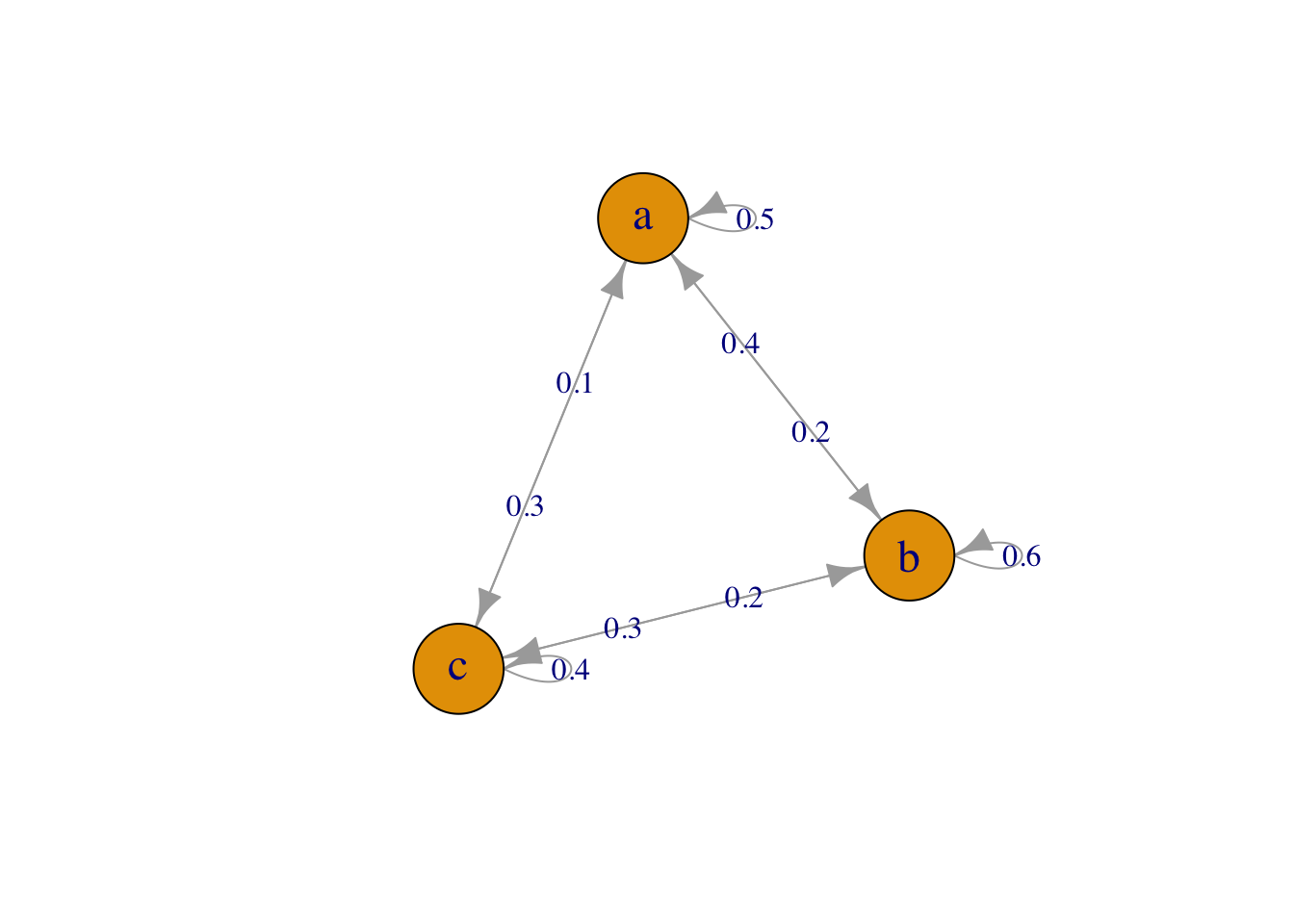
Figura 36.1: Cadeia de Markov com 3 estados (a, b, c) e suas probabilidades de transição.

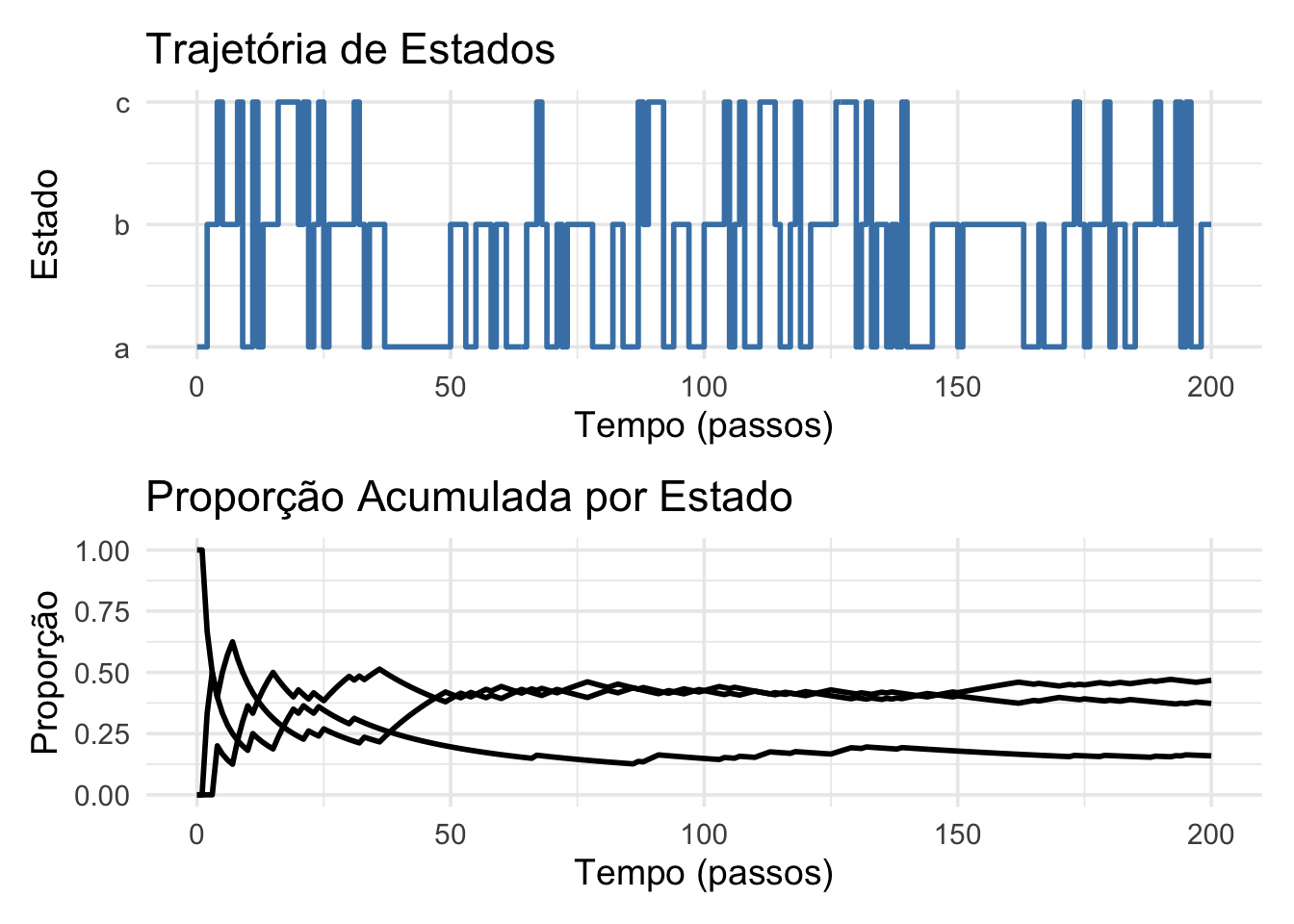
Figura 36.2: Trajetória de estados e proporção acumulada por estado em uma cadeia de Markov com 3 estados (a, b, c).

O pacote markovchain³²⁹ fornece a função markovchainFit ajusta uma cadeia com base em dados observados.

36.3 Efeito fixo

36.3.1 O que é efeito fixo?

Efeito fixo é a relação média entre variáveis assumida como igual para todos os grupos ou indivíduos, representando o comportamento populacional esperado.^REF?
Ele descreve tendências sistemáticas e reprodutíveis que não dependem de pertencer a um grupo específico.^REF?
Em modelos estatísticos, corresponde aos parâmetros estimados globalmente a partir de todos os dados.^REF?

36.4 Efeito aleatório

36.4.1 O que é efeito aleatório?

Efeito aleatório representa desvios específicos de grupos ou unidades em relação ao efeito fixo.^REF?
Ele modela a variabilidade entre grupos, assumindo que esses desvios são amostras de uma distribuição comum.^REF?
Não busca estimar cada grupo isoladamente, mas sim quantificar a variabilidade entre eles.^REF?

36.5 Efeito misto

36.5.1 O que é efeito misto?

Um modelo de efeitos mistos combina efeitos fixos e aleatórios em uma única estrutura estatística.^REF?
Ele permite estimar tendências globais ao mesmo tempo em que ajusta variações específicas por grupo.^REF?
Essa combinação possibilita inferência correta mesmo na presença de heterogeneidade, evitando armadilhas como o Paradoxo de Simpson.^REF?

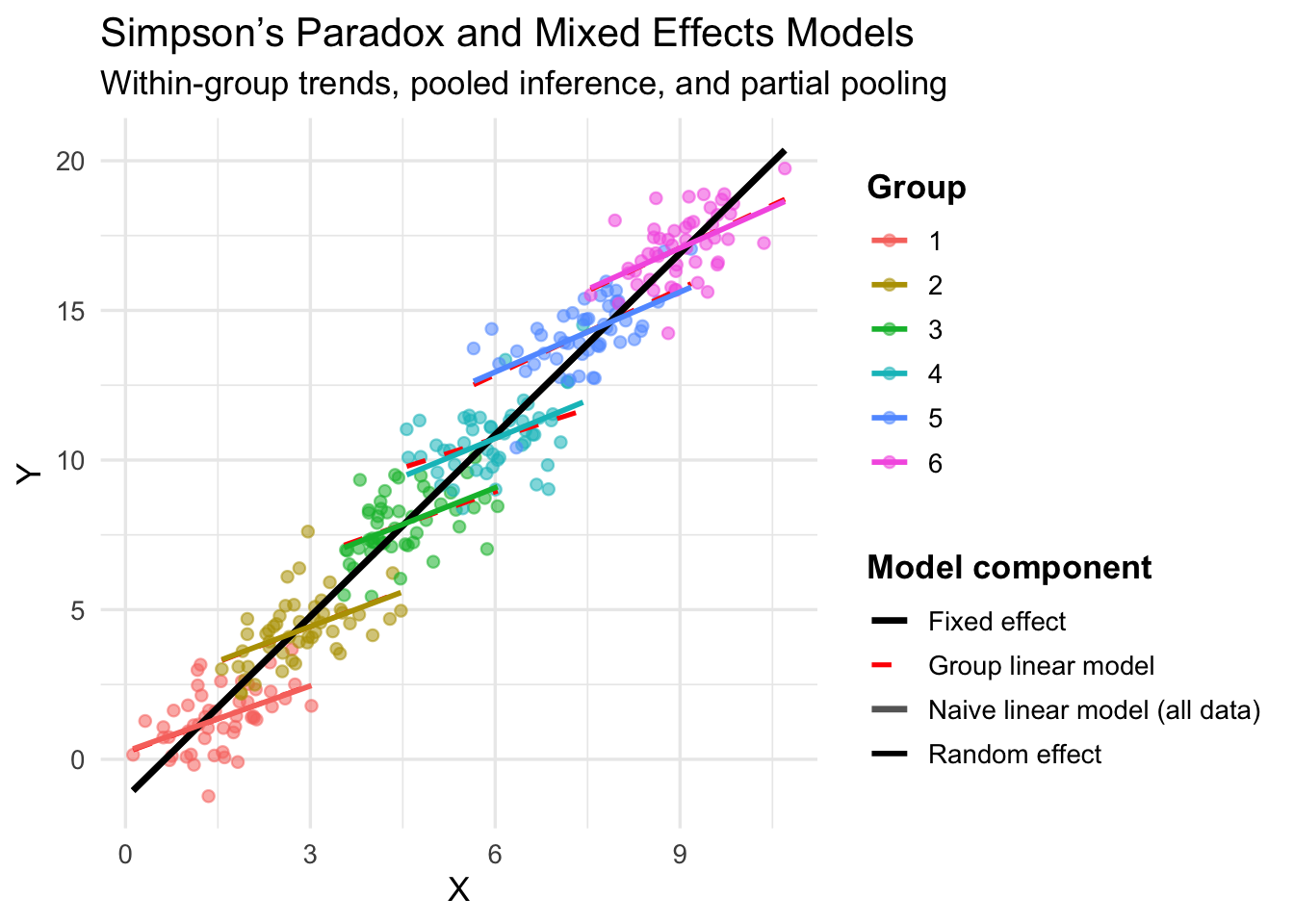
Efeitos fixos, aleatórios e mistos em dados simulados com paradoxo de Simpson. As linhas vermelhas representam os efeitos dentro dos grupos, enquanto as linhas cinza e preta representam os efeitos globais (naive e fixo, respectivamente). O modelo misto (linhas coloridas) captura os efeitos dentro dos grupos sem extrapolar além dos dados observados.

Figura 36.3: Efeitos fixos, aleatórios e mistos em dados simulados com paradoxo de Simpson. As linhas vermelhas representam os efeitos dentro dos grupos, enquanto as linhas cinza e preta representam os efeitos globais (naive e fixo, respectivamente). O modelo misto (linhas coloridas) captura os efeitos dentro dos grupos sem extrapolar além dos dados observados.

36.6 Efeito principal

36.6.1 O que é efeito principal?

.³³⁰

36.7 Efeito de interação

36.7.1 O que é efeito de interação?

A interação - representada pelo símbolo * - é o termo estatístico empregado para representar a heterogeneidade de um determinado efeito.³³¹
.³³⁰

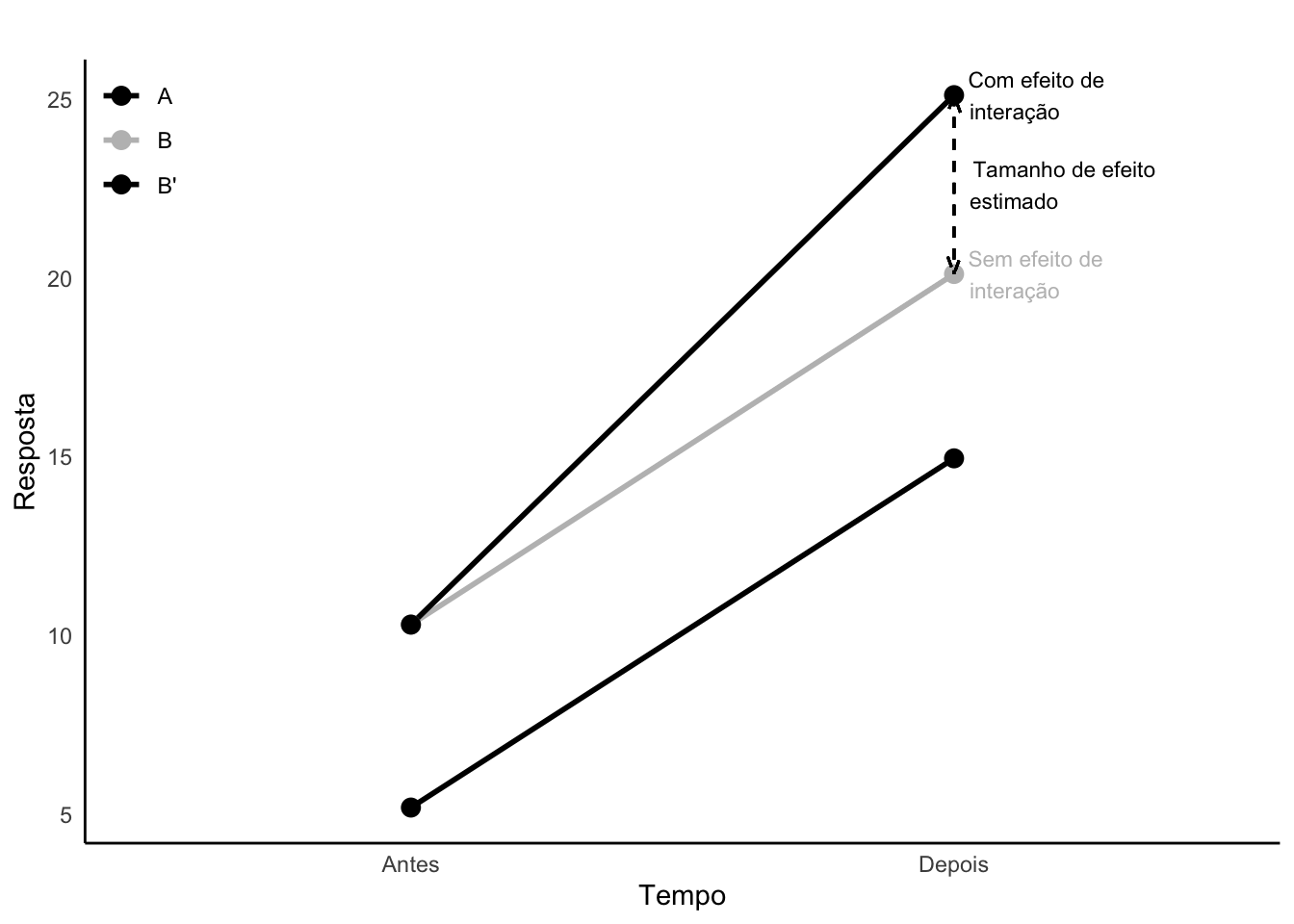
Figura 36.4: Análise de efeito de interação (direta) entre grupos e tempo. Retas paralelas sugerem ausência de efeito de interação.

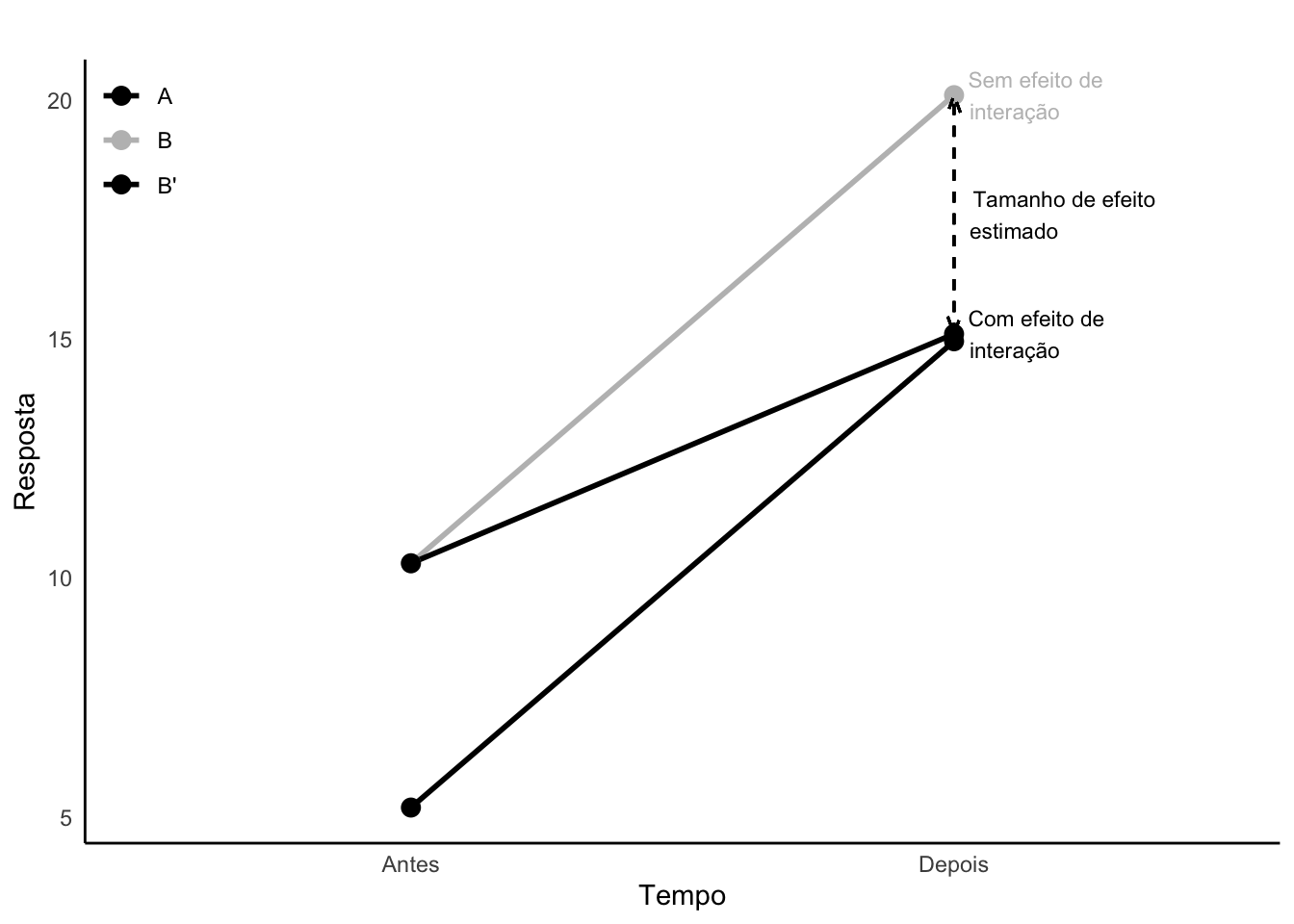
Figura 36.5: Análise de efeito de interação (inversa) entre grupos e tempo. Retas paralelas sugerem ausência de efeito de interação.

O pacote nlme³³² fornece a função nlme para ajustar um modelo de regressão misto não linear.

O pacote mmrm³³³ fornece a função mmrm para ajuste de um modelo de regressão misto linear.

O pacote emmeans³³⁴ fornece a função emmeans para calcular as médias marginais dos fatores e suas combinações de um modelo de regressão misto linear.

36.8 Efeito de mediação

36.8.1 O que é um mediador de efeito?

.³³⁵
.³³⁰

36.8.2 O que é efeito de mediação?

.³³⁵
.³³⁰

36.8.3 O que é efeito direto?

.³³⁵
.³³⁰

36.8.4 O que é efeito indireto?

.³³⁵
.³³⁰

36.8.5 O que é efeito total?

.³³⁵
.³³⁰

36.9 Efeito de modificação

36.9.1 O que é um modificador de efeito?

.³³⁰

36.9.2 O que é efeito de modificação?

.³³⁰

36.10 Preditores e desfechos

36.11 Desempenho e estabilidade de modelos

36.11.1 Como avaliar o desempenho dos modelos?

Pela área sob a curva ROC em conjunto com o otimismo (diferença entre AUC aparente e validada).³²⁷
O desempenho melhora com maior tamanho amostral, mas de forma desigual entre técnicas.³²⁷

36.11.2 Qual modelo alcança estabilidade mais rapidamente?

Regressão logística é o mais estável e menos data hungry.³²⁷
Árvore de decisão para classificação e regressão estabiliza rápido, mas em nível de desempenho baixo.³²⁷
Máquina de vetores de suporte, redes neurais e random forests apresentam instabilidade mesmo em amostras muito grandes.³²⁷

36.12 Comparação de modelos

36.12.1 Como comparar modelos estatísticos?

.^REF?

36.12.2 Como comparar modelos de aprendizagem de máquina?

.^REF?

O pacote correctR³³⁶ fornece funções para comparar o desempenho e a qualidade do ajuste de diversos modelos de aprendizagem de máquina em amostras correlacionadas.

36.13 Avaliação de modelos

36.13.1 Como avaliar a qualidade de ajuste de um modelo?

Coeficiente de determinação ($R^2$) (36.1) e $R^2$ ajustado (36.2): Medem a proporção da variabilidade dos dados explicada pelo modelo. O $R^2$ ajustado penaliza a inclusão de variáveis irrelevantes.^REF?

\[\begin{equation} \tag{36.1} R^2 = 1 - \frac{SS_{res}}{SS_{tot}} \end{equation}\]

\[\begin{equation} \tag{36.2} R^2_{ajustado} = 1 - (1 - R^2)\frac{n - 1}{n - p - 1} \end{equation}\]

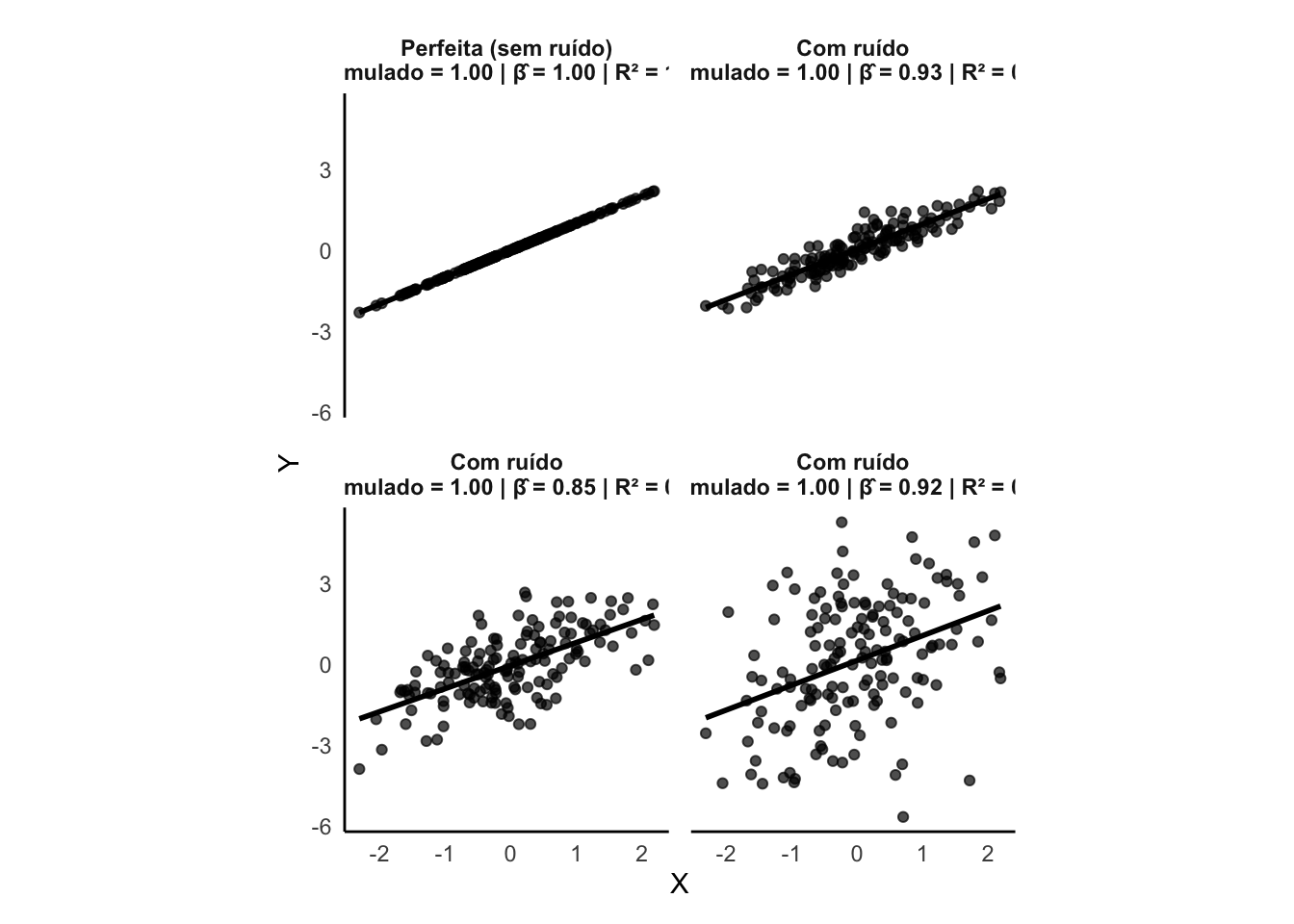
$Exemplos de ajuste de modelos de regressão linear simples ($y \sim x$) com diferentes níveis de ruído ($R^2$). Cada painel mostra a reta ajustada (cinza) e os valores observados (pontos). Os valores anotados indicam o coeficiente angular simulado ($\beta$), o coeficiente angular estimado ($\hat{\beta}$) e o $R^2$ observado.$

Figura 36.6: Exemplos de ajuste de modelos de regressão linear simples ($y \sim x$) com diferentes níveis de ruído ($R^2$). Cada painel mostra a reta ajustada (cinza) e os valores observados (pontos). Os valores anotados indicam o coeficiente angular simulado ($\beta$), o coeficiente angular estimado ($\hat{\beta}$) e o $R^2$ observado.

Erro quadrático médio ($RMSE$) (36.3): Mede a média dos erros ao quadrado entre os valores observados e os valores previstos pelo modelo, onde $y_i$ são os valores observados, $\hat{y}_i$ são os valores previstos pelo modelo, e $n$ é o número de observações. Valores menores indicam melhor ajuste.^REF?

\[\begin{equation} \tag{36.3} RMSE = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2} \end{equation}\]

Critério de Informação Akaike ($AIC$) (36.4) e Critério de Informação Bayesiano ($BIC$) (36.5): Avaliam o ajuste do modelo penalizando a complexidade (número de parâmetros), onde $k$ é o número de parâmetros do modelo, $L$ é a verossimilhança máxima do modelo, e $n$ é o tamanho da amostra. Modelos com menor AIC ou BIC são preferíveis.^REF?

\[\begin{equation} \tag{36.4} AIC = 2k - 2\ln(L) \end{equation}\]

\[\begin{equation} \tag{36.5} BIC = \ln(n)k - 2\ln(L) \end{equation}\]

Desvio residual ($\sigma$): Mede a variabilidade dos resíduos do modelo. Valores menores indicam melhor ajuste.^REF?

Tabela 36.1: Métricas de desempenho do modelo de regressão linear.
Métrica	Valor
AIC	513.017
AIC corrigido	513.267
BIC	520.833
$R^2$	0.007
$R^2$ ajustado	-0.003
Erro quadrático médio (RMSE)	3.053
Desvio residual (sigma)	3.084

O pacote performance²⁵³ fornece a função model_performance para calcular as métricas de ajuste da regressão adequadas ao modelo pré-especificado.

O pacote performance²⁵³ fornece a função compare_performance para comparar o desempenho e a qualidade do ajuste de diversos modelos de regressão pré-especificados.

36.14 Validação de modelos

36.14.1 Como validar modelos estatísticos?

.^REF?

36.15 Calibração de modelos

36.15.1 Como calibrar modelos estatísticos?

.^REF?

Citar como:
Ferreira, Arthur de Sá. Ciência com R: Perguntas e respostas para pesquisadores e analistas de dados. Rio de Janeiro: 1a edição,

Referências

253.

Lüdecke D, Ben-Shachar MS, Patil I, Waggoner P, Makowski D. performance: An R Package for Assessment, Comparison and Testing of Statistical Models. Journal of Open Source Software. 2021;6:3139. doi:10.21105/joss.03139

255.

Greenland S. Modeling and variable selection in epidemiologic analysis. American Journal of Public Health. 1989;79(3):340–349. doi:10.2105/ajph.79.3.340

325.

Box GEP. Science and Statistics. Journal of the American Statistical Association. 1976;71(356):791–799. doi:10.1080/01621459.1976.10480949

326.

Anderson D, Heiss A, Sumners J. equatiomatic: Transform Models into LaTeX Equations.; 2024. https://CRAN.R-project.org/package=equatiomatic.

327.

Ploeg T van der, Austin PC, Steyerberg EW. Modern modelling techniques are data hungry: a simulation study for predicting dichotomous endpoints. BMC Medical Research Methodology. 2014;14(1). doi:10.1186/1471-2288-14-137

329.

Spedicato GA. Discrete Time Markov Chains with R. The R Journal. 2017;9(2):84–104. doi:10.32614/RJ-2017-036

330.

Bours MJL. Using mediators to understand effect modification and interaction. Journal of Clinical Epidemiology. setembro 2023. doi:10.1016/j.jclinepi.2023.09.005

331.

Altman DG, Matthews JNS. Statistics Notes: Interaction 1: heterogeneity of effects. BMJ. 1996;313(7055):486–486. doi:10.1136/bmj.313.7055.486

332.

Pinheiro J, Bates D, R Core Team. nlme: Linear and Nonlinear Mixed Effects Models.; 2023. https://CRAN.R-project.org/package=nlme.

333.

Sabanes Bove D, Dedic J, Kelkhoff D, et al. mmrm: Mixed Models for Repeated Measures.; 2022. https://CRAN.R-project.org/package=mmrm.

334.

Lenth RV. emmeans: Estimated Marginal Means, aka Least-Squares Means.; 2023. https://CRAN.R-project.org/package=emmeans.

335.

Baron RM, Kenny DA. The moderatormediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of Personality and Social Psychology. 1986;51(6):1173–1182. doi:10.1037/0022-3514.51.6.1173

336.

Henderson T. correctR: Corrected Test Statistics for Comparing Machine Learning Models on Correlated Samples.; 2025. https://CRAN.R-project.org/package=correctR.