Capítulo 35 Redes

35.1 Análise de redes

35.1.1 O que é análise de rede?

• A análise de redes é uma abordagem estatística gráfica baseada na teoria dos grafos que permite representar, explorar e interpretar relações complexas entre múltiplas variáveis analisadas simultaneamente.³²⁰

• Nessa abordagem, as variáveis são representadas por nodos (ou nós) e as relações entre elas por arestas, formando uma estrutura relacional que evidencia padrões de associação, interdependência e organização do sistema estudado.³²⁰

• Diferentemente de métodos tradicionais, como análises univariadas ou modelos de regressão clássicos, a análise de redes não foca relações isoladas entre variáveis, mas sim o comportamento conjunto do sistema, permitindo observar fenômenos emergentes que não seriam detectáveis individualmente.³²⁰

• A análise de redes representa uma mudança conceitual importante em relação às abordagens estatísticas tradicionais, ao enfatizar sistemas, interações e complexidade.³²⁰

35.1.2 Por que a análise de redes é útil em pesquisa científica?

• Muitos fenômenos científicos, especialmente nas ciências da saúde, são multifatoriais, interdependentes e não lineares, envolvendo variáveis biológicas, comportamentais, psicológicas e sociais.³²⁰

• Análises univariadas tendem a simplificar esses fenômenos ao avaliar efeitos médios ou relações diretas entre pares de variáveis, o que pode ocultar padrões relevantes.³²⁰

• A análise de redes permite: visualizar associações simultâneas entre diversas variáveis; identificar variáveis centrais em um sistema; detectar subestruturas densas ou agrupamentos de variáveis fortemente associadas; explorar potenciais mecanismos intermediários ou mediadores.³²⁰

35.1.3 Quais são as limitações da análise de redes?

Apesar de seu potencial, a interpretação dos resultados deve ser cuidadosa, especialmente em estudos observacionais, evitando inferências causais indevidas.³²⁰

35.2 Matriz de incidência

35.2.1 O que é uma matriz de incidência?

• Uma matriz de incidência é uma representação tabular que descreve a relação entre dois conjuntos distintos de entidades, como nodos e arestas em uma rede.³²⁰

• Em uma matriz de incidência, as linhas representam um conjunto de entidades (nodos) e as colunas representam outro conjunto (arestas). A presença ou ausência de uma relação entre as entidades é indicada por valores binários (0 ou 1) ou por pesos numéricos que refletem a intensidade da relação.³²⁰

Tabela 35.1: Exemplo de dados categóricos para criação de matriz de incidência.

Sexo	Tabagismo	Atividade
F	Sim	Baixa
M	Não	Alta
F	Não	Moderada
F	Sim	Baixa
M	Não	Alta

Code

# Exemplo dados categóricos
dados_cat <- data.frame(
  Sexo      = c("F", "M", "F", "F", "M"),
  Tabagismo = c("Sim", "Não", "Não", "Sim", "Não"),
  Atividade = c("Baixa", "Alta", "Moderada", "Baixa", "Alta")
)

# Matriz de incidência (one-hot encoding)
matriz_incidencia <- model.matrix(
  ~ Sexo + Tabagismo + Atividade - 1,
  data = dados_cat
)

# Converter para data.frame
matriz_incidencia <- as.data.frame(matriz_incidencia)

# exibe a tabela de dados
knitr::kable(
  matriz_incidencia,
  align = "c",
  format = ifelse(knitr::is_html_output(), "html", "latex"),
  booktabs = TRUE,
  linesep = "",
  escape = FALSE
) %>%
  kableExtra::kable_styling(
    latex_options = c("basic"),
    bootstrap_options = c("basic", "hover", "condensed", "responsive"),
    full_width = ifelse(knitr::is_html_output(), T, T),
    position = "center"
  ) %>%
  kableExtra::row_spec(0, bold = TRUE, extra_css = "border-top: 1px solid; border-bottom: 1px solid") %>%
  kableExtra::column_spec(1, bold = TRUE) %>%
  kableExtra::row_spec(dim(matriz_incidencia)[1], extra_css = "border-bottom: 1px solid")

Tabela 35.2: Matriz de incidência criada a partir de dados categóricos.

SexoF	SexoM	TabagismoSim	AtividadeBaixa	AtividadeModerada
1	0	1	1	0
0	1	0	0	0
1	0	0	0	1
1	0	1	1	0
0	1	0	0	0

O pacote stats¹³⁴ fornece a função model.matrix para criar uma matrix de incidência por expansão de variáveis indicadoras.

35.3 Elementos da rede

35.3.1 Quais são os principais elementos de uma rede?

• Nodos (nós): representam as variáveis do estudo, como sintomas, doenças, características clínicas, sociais ou psicológicas.³²⁰

• Arestas: representam as relações entre os nodos. Podem indicar correlação, associação parcial, dependência condicional ou outro tipo de relação estatística.³²⁰

• Peso das arestas: em redes ponderadas, a espessura da aresta indica a magnitude da relação; relações mais fortes são representadas por conexões mais espessas.³²⁰

• Sinal das arestas: geralmente codificado por cores, indicando associações positivas ou negativas.³²⁰

Code

# Definir arestas com peso e sinal
edges <- data.frame(
  from   = c("A", "A", "B", "C", "D"),
  to     = c("B", "C", "C", "D", "A"),
  peso   = c( 0.8, -0.5,  0.6, -0.7,  0.4)
)

g <- igraph::graph_from_data_frame(edges, directed = FALSE)

# Peso absoluto define espessura da aresta
igraph::E(g)$width <- abs(igraph::E(g)$peso) * 4

# Cor indica sinal da relação
igraph::E(g)$color <- ifelse(igraph::E(g)$peso > 0, "steelblue", "firebrick")

# Rótulo das arestas (valor do peso)
igraph::E(g)$label <- round(igraph::E(g)$peso, 2)
igraph::E(g)$label.color <- "black"
igraph::E(g)$label.cex <- 0.8

# Nós
igraph::V(g)$size <- 30
igraph::V(g)$color <- "grey85"
igraph::V(g)$frame.color <- "black"
igraph::V(g)$label.cex <- 1.1
igraph::V(g)$label.color <- "black"

set.seed(123)
layout_fr <- igraph::layout_with_fr(g)

plot(
  g,
  layout = layout_fr,
  vertex.label = igraph::V(g)$name,
  edge.label = igraph::E(g)$label
)
legend(
  "topleft",
  inset = 0.02,
  title = "Legend",
  legend = c(
    "Node (variable)",
    "Positive edge",
    "Negative edge",
    "Edge width ∝ |weight|"
  ),
  pch = c(21, NA, NA, NA),
  pt.bg = c("grey85", NA, NA, NA),
  lty = c(NA, 1, 1, 1),
  lwd = c(NA, 2, 2, 4),
  col = c("black", "steelblue", "firebrick", "black"),
  bty = "n",
  cex = 0.9
)

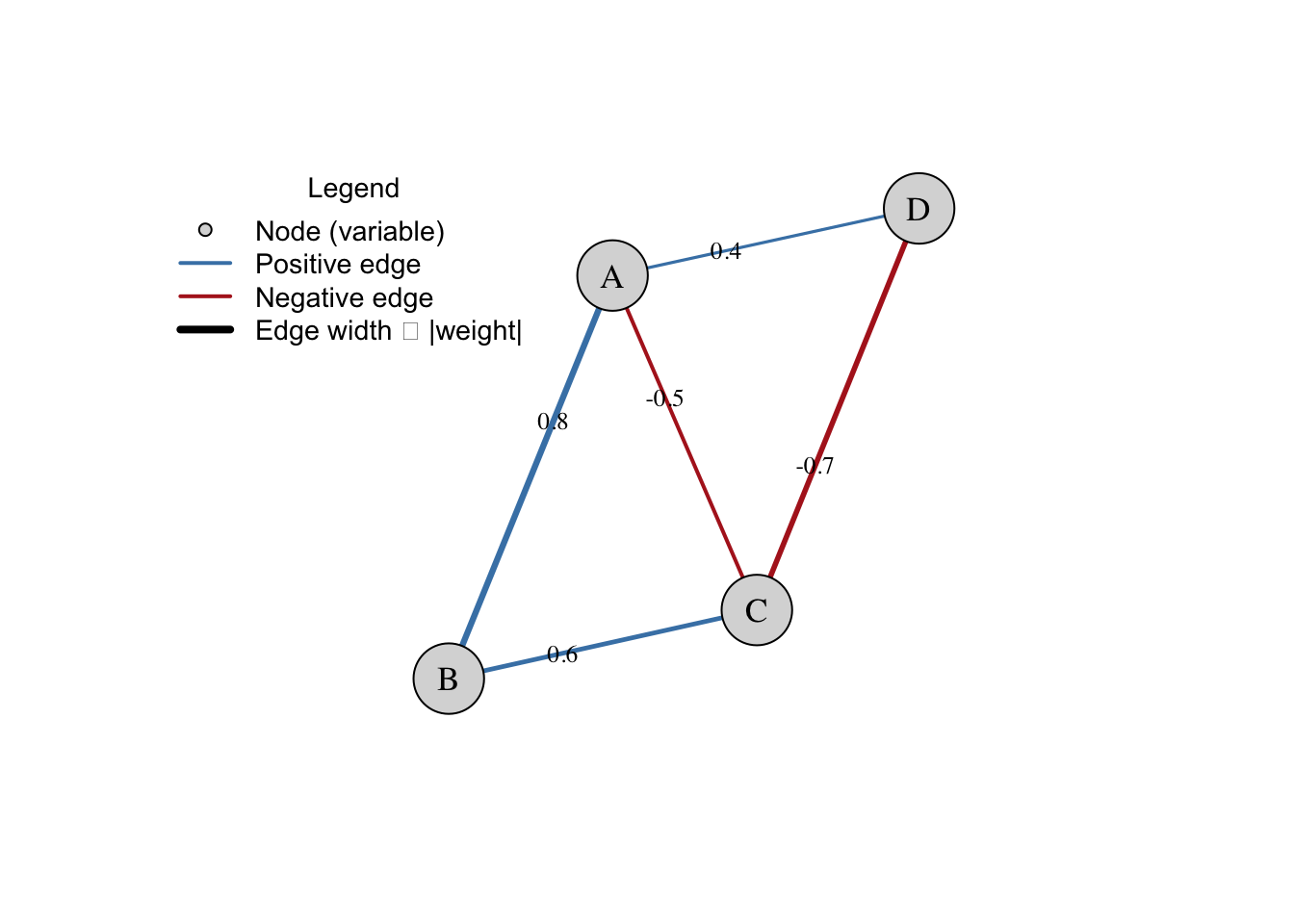
Figura 35.1: Exemplo de grafo de rede com nodos e arestas ponderadas.

35.3.2 Como as redes podem ser classificadas?

• Redes não ponderadas: indicam apenas a presença ou ausência de relação entre os nodos.³²⁰

• Redes ponderadas: representam também a intensidade da relação.³²⁰

• Redes direcionais: possuem setas nas arestas, indicando direção da relação (por exemplo, causalidade hipotética).³²⁰

• Redes não direcionais: não assumem direção causal e são mais apropriadas para estudos observacionais e transversais.³²⁰

• Em pesquisas transversais, especialmente em saúde, redes não direcionais e ponderadas são geralmente preferidas, pois evitam inferências causais indevidas quando não há informação temporal adequada.³²⁰

35.3.3 O que define a posição dos nodos em um grafo de rede?

• A posição espacial dos nodos é determinada por algoritmos de disposição (layout), que organizam a rede de modo a facilitar a interpretação visual.³²⁰

• Um dos algoritmos mais utilizados é o Fruchterman–Reingold³²¹, que simula forças de atração e repulsão entre os nodos, posicionando nodos mais fortemente associados mais próximos entre si. A proximidade entre nodos em um grafo geralmente reflete maior associação estatística.³²⁰

35.4 Tipos de redes

35.4.1 Quais são os principais tipos de redes estatísticas?

• Redes de correlação: baseadas em matrizes de correlação simples; são fáceis de interpretar, mas podem conter associações espúrias.³²⁰

• Redes de correlação parcial: representam relações entre dois nodos controlando todas as demais variáveis do sistema, reduzindo associações indiretas.³²⁰

• Modelos gráficos gaussianos: uma forma específica de rede de correlação parcial, muito utilizada em psicometria e epidemiologia.³²⁰

• Modelos gráficos mistos: permitem a análise conjunta de variáveis contínuas, ordinais e dicotômicas, comuns em dados reais de saúde.³²⁰

35.4.2 Como reduzir associações espúrias em redes?

• Em conjuntos de dados com muitas variáveis, redes podem se tornar densas e difíceis de interpretar. Para contornar esse problema, utiliza-se penalização estatística, como o método LASSO (Least Absolute Shrinkage and Selection Operator).³²⁰

• Na análise de redes, o Graphical LASSO (gLASSO) elimina associações fracas, resultando em redes mais parcimoniosas e interpretáveis.³²⁰

35.5 Métricas de rede

35.5.1 O que são medidas de centralidade?

• Medidas de centralidade quantificam a importância relativa de cada nodo no sistema.³²⁰

• Grau: número de conexões diretas de um nodo.³²⁰

• Força: soma dos pesos das conexões de um nodo, sendo uma das medidas mais utilizadas em redes ponderadas.³²⁰

• Intermediação: frequência com que um nodo atua como ponte entre outros nodos.³²⁰

• Proximidade: quão próximo um nodo está de todos os outros.³²⁰

• Agrupamento: tendência de um nodo formar grupos com seus vizinhos.³²⁰

Code

edges <- data.frame(
  from = c("A", "A", "B", "C", "D"),
  to   = c("B", "C", "C", "D", "A"),
  peso = c( 0.8, -0.5,  0.6, -0.7,  0.4)
)

g <- igraph::graph_from_data_frame(edges, directed = FALSE)

# Separar semântica
igraph::E(g)$peso      <- edges$peso
igraph::E(g)$abs_peso  <- abs(edges$peso)

# Força dos nós
forca <- igraph::strength(g, weights = igraph::E(g)$abs_peso)

# Escalar tamanho do nó pela força
igraph::V(g)$size <- 20 + 30 * (forca / max(forca))

# Cor neutra para nós
igraph::V(g)$color <- "grey85"
igraph::V(g)$frame.color <- "black"

# Arestas
igraph::E(g)$width <- igraph::E(g)$abs_peso * 4
igraph::E(g)$color <- ifelse(igraph::E(g)$peso > 0, "steelblue", "firebrick")

# Layout correto (somente pesos positivos)
set.seed(123)
layout_fr <- igraph::layout_with_fr(g, weights = igraph::E(g)$abs_peso)

plot(
  g,
  layout = layout_fr,
  vertex.label = paste0(igraph::V(g)$name),
  edge.label   = round(igraph::E(g)$peso, 2)
)

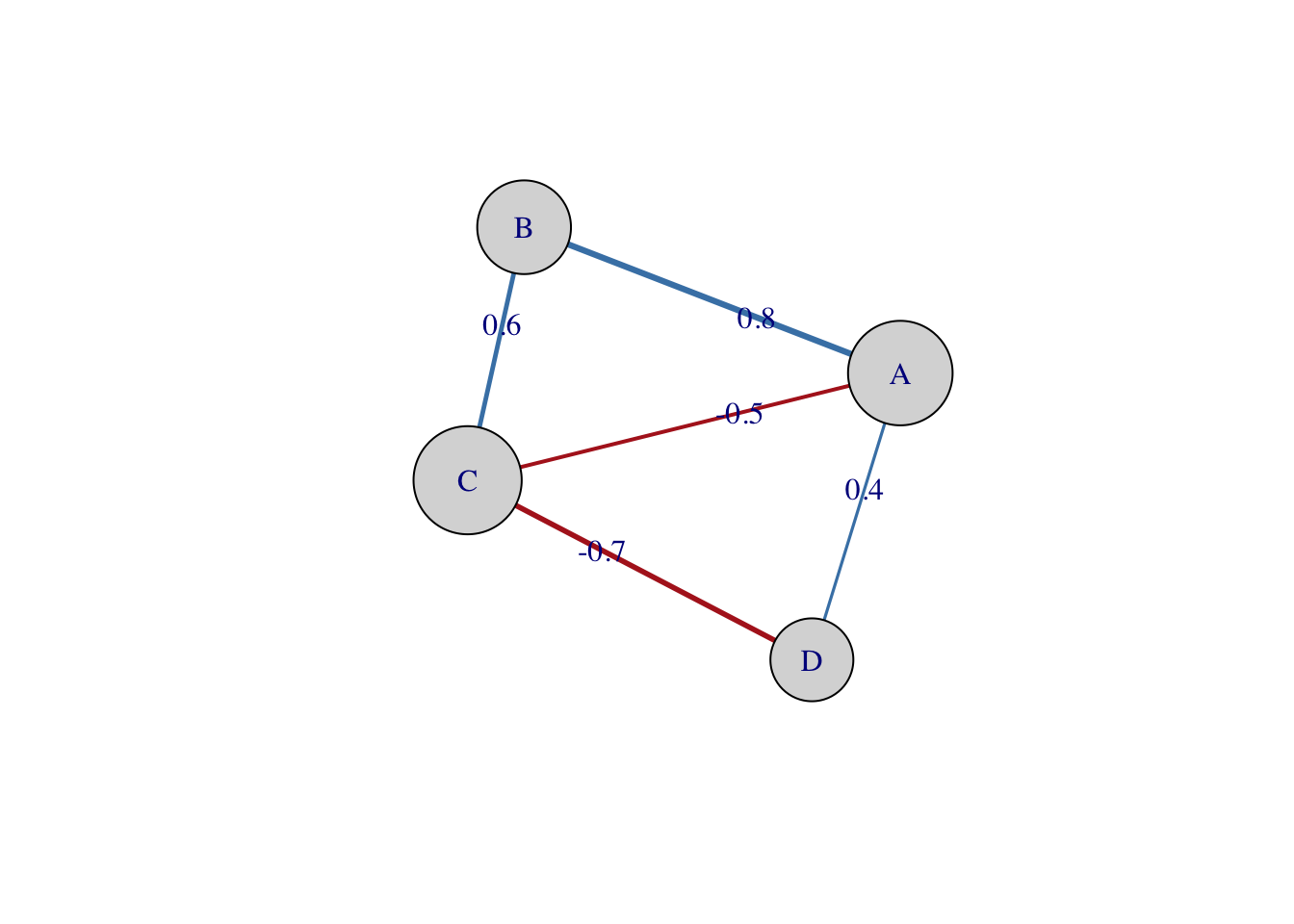
Figura 35.2: Exemplo de grafo de rede com tamanho dos nodos proporcional à força.

Code

edges <- data.frame(
  from = c("A", "A", "B", "C", "D"),
  to   = c("B", "C", "C", "D", "A"),
  peso = c( 0.8, -0.5,  0.6, -0.7,  0.4)
)

g <- igraph::graph_from_data_frame(edges, directed = FALSE)

grau <- igraph::degree(g)

forca <- igraph::strength(g, weights = igraph::E(g)$abs_peso)

intermediacao <- igraph::betweenness(
  g,
  weights = 1 / igraph::E(g)$abs_peso,
  normalized = TRUE
)

proximidade <- igraph::closeness(
  g,
  weights = 1 / igraph::E(g)$abs_peso,
  normalized = TRUE
)

agrupamento <- igraph::transitivity(
  g,
  type = "local",
  isolates = "zero"
)

# Converter para data.frame
metricas <- data.frame(
  Nó = names(grau),
  Grau = grau,
  Força = round(forca, 2),
  Intermediação = round(intermediacao, 3),
  Proximidade = round(proximidade, 3),
  Agrupamento = round(agrupamento, 3)
)

# exibe a tabela de dados
knitr::kable(
  metricas,
  align = "c",
  format = ifelse(knitr::is_html_output(), "html", "latex"),
  booktabs = TRUE,
  linesep = "",
  escape = FALSE
) %>%
  kableExtra::kable_styling(
    latex_options = c("basic"),
    bootstrap_options = c("basic", "hover", "condensed", "responsive"),
    full_width = ifelse(knitr::is_html_output(), T, T),
    position = "center"
  ) %>%
  kableExtra::row_spec(0, bold = TRUE, extra_css = "border-top: 1px solid; border-bottom: 1px solid") %>%
  kableExtra::column_spec(1, bold = TRUE) %>%
  kableExtra::row_spec(dim(metricas)[1], extra_css = "border-bottom: 1px solid")

Tabela 35.3: Tabela com principais métricas de centralidade dos nodos.

	Nó	Grau	Força	Intermediação	Proximidade	Agrupamento
A	A	3	3	0.167	1.00	0.667
B	B	2	2	0.000	0.75	1.000
C	C	3	3	0.167	1.00	0.667
D	D	2	2	0.000	0.75	1.000

O pacote igraph³²² fornece a função graph_from_incidence_matrix para criar uma rede a partir de uma matriz de incidência.

O pacote bootnet³²³ fornece a função bootnet para avaliação da estabilidade e precisão das redes por reamostragem.

O pacote mgm³²⁴ fornece a função mgm para estimação de modelos gráficos mistos.

Citar como:
Ferreira, Arthur de Sá. Ciência com R: Perguntas e respostas para pesquisadores e analistas de dados. Rio de Janeiro: 1a edição,

Referências

134.

R Core Team. R: A Language and Environment for Statistical Computing.; 2025. https://www.R-project.org/.

320.

Leme DE da C, Alves EV da C, Lemos V do CO, Fattori A. NETWORK ANALYSIS: A MULTIVARIATE STATISTICAL APPROACH FOR HEALTH SCIENCE RESEARCH. Geriatrics, Gerontology and Aging. 2020;14(1):43–51. doi:10.5327/z2447-212320201900073

321.

Fruchterman TMJ, Reingold EM. Graph drawing by force-directed placement. Software: Practice and Experience. 1991;21(11):1129–1164. doi:10.1002/spe.4380211102

322.

Csárdi G, Nepusz T. The igraph software package for complex network research. Vol Complex Systems.; 2006:1695. https://igraph.org.

323.

Epskamp S, Borsboom D, Fried EI. Estimating Psychological Networks and their Accuracy: A Tutorial Paper. Vol 50.; 2018.

324.

Haslbeck JMB, Waldorp LJ. mgm: Estimating Time-Varying Mixed Graphical Models in High-Dimensional Data. Vol 93.; 2020. doi:10.18637/jss.v093.i08