Capítulo 51 Desempenho diagnóstico

51.1 Características

51.1.1 Quais são as características de estudos de desempenho diagnóstico?

• .^REF?

51.2 Tabelas 2x2

51.2.1 O que é uma tabela de confusão 2x2?

• Tabela de confusão é uma matriz de 2 linhas por 2 colunas que permite analisar o desempenho de classificação de uma variável dicotômica (padrão-ouro ou referência) versus outra variável dicotômica (novo teste).³⁹⁸

51.2.2 Como analisar o desempenho diagnóstico em tabelas 2x2?

• Verdadeiro-positivo (\(VP\)): caso com a condição presente e corretamente identificado como tal.³⁹⁹

• Falso-negativo (\(FN\)): caso com a condição presente e erroneamente identificado como ausente.³⁹⁹

• Verdadeiro-negativo (\(VN\)): controle sem a condição presente e corretamente identificados como tal.³⁹⁹

• Falso-positivo (\(FP\)): controle sem a condição presente e erroneamente identificado como presente.³⁹⁹

Tabela 51.1: Tabela de confusão 2x2 para análise de desempenho diagnóstico de testes e variáveis dicotômicas.

	Condição presente	Condição ausente	Total
Teste positivo	\(VP\)	\(FP\)	\(VP+FP\)
Teste negativo	\(FN\)	\(VN\)	\(FN+VN\)
Total	\(VP+FN\)	\(FP+VN\)	\(N=VP+VN+FP+FN\)

• Tabelas de confusão também podem ser visualizadas em formato de árvores de frequência.³⁹⁸

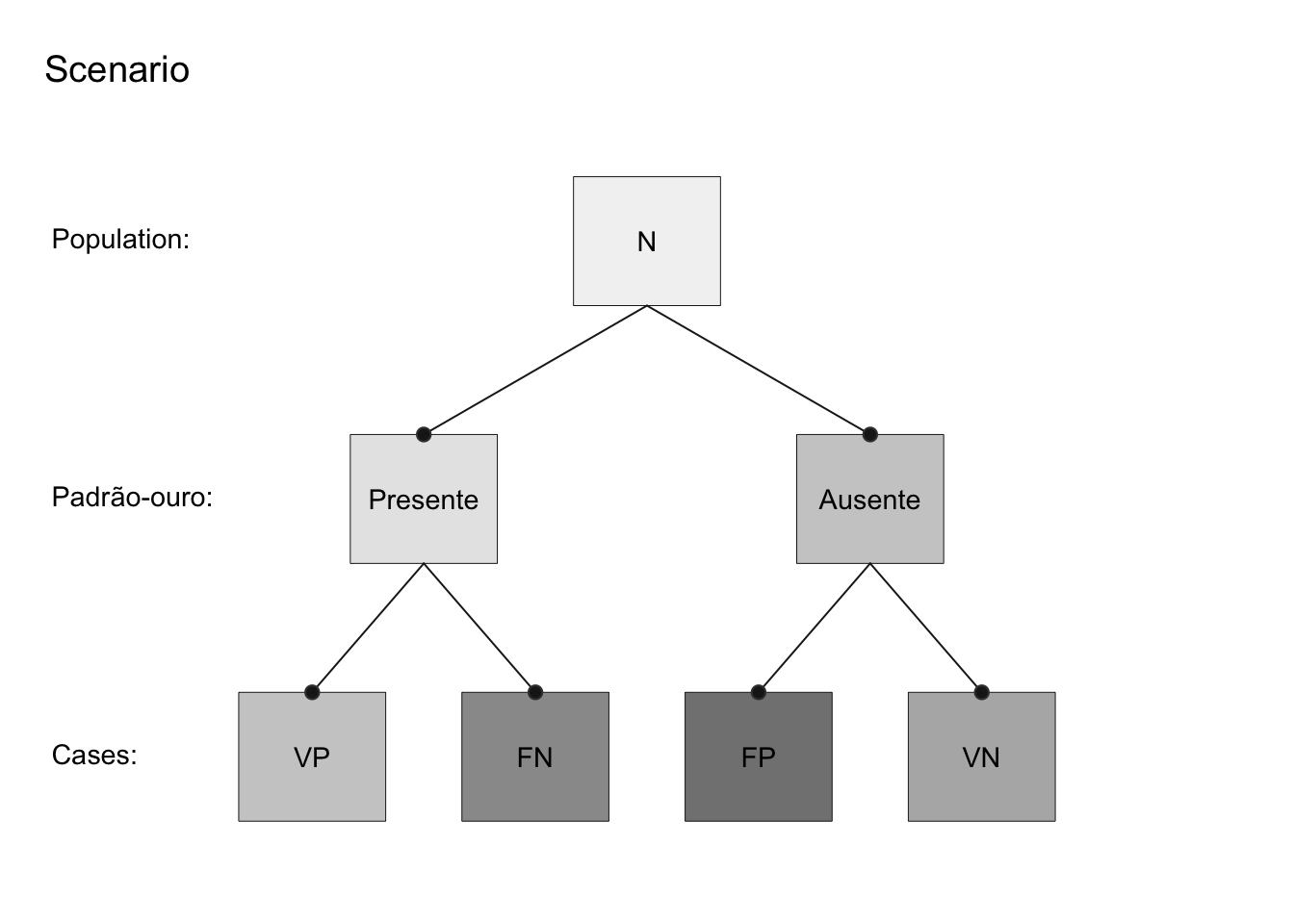
Figura 51.1: Árvore de frequência do desempenho diagnóstico de uma tabela de confusão 2x2 representando um método novo (dicotômico) comparado ao método padrão-ouro ou referência (dicotômico).

O pacote riskyr⁴⁰⁰ fornece a função plot_prism para construir árvores de frequência a partir de diferentes cenários.

51.2.3 Quais probabilidades caracterizam o desempenho diagnóstico de um teste em tabelas 2x2?

• Sensibilidade (\(SEN\)) (51.1): Proporção de verdadeiro-positivos dentre aqueles com a condição.³⁹⁹

\[\begin{equation} \tag{51.1} SEN = \dfrac{VP}{VP+FN} \end{equation}\]

• Especificidade (\(ESP\)) (51.2): Proporção de verdadeiro-negativos dentre aqueles sem a condição.³⁹⁹

\[\begin{equation} \tag{51.2} ESP = \dfrac{VN}{VN+FP} \end{equation}\]

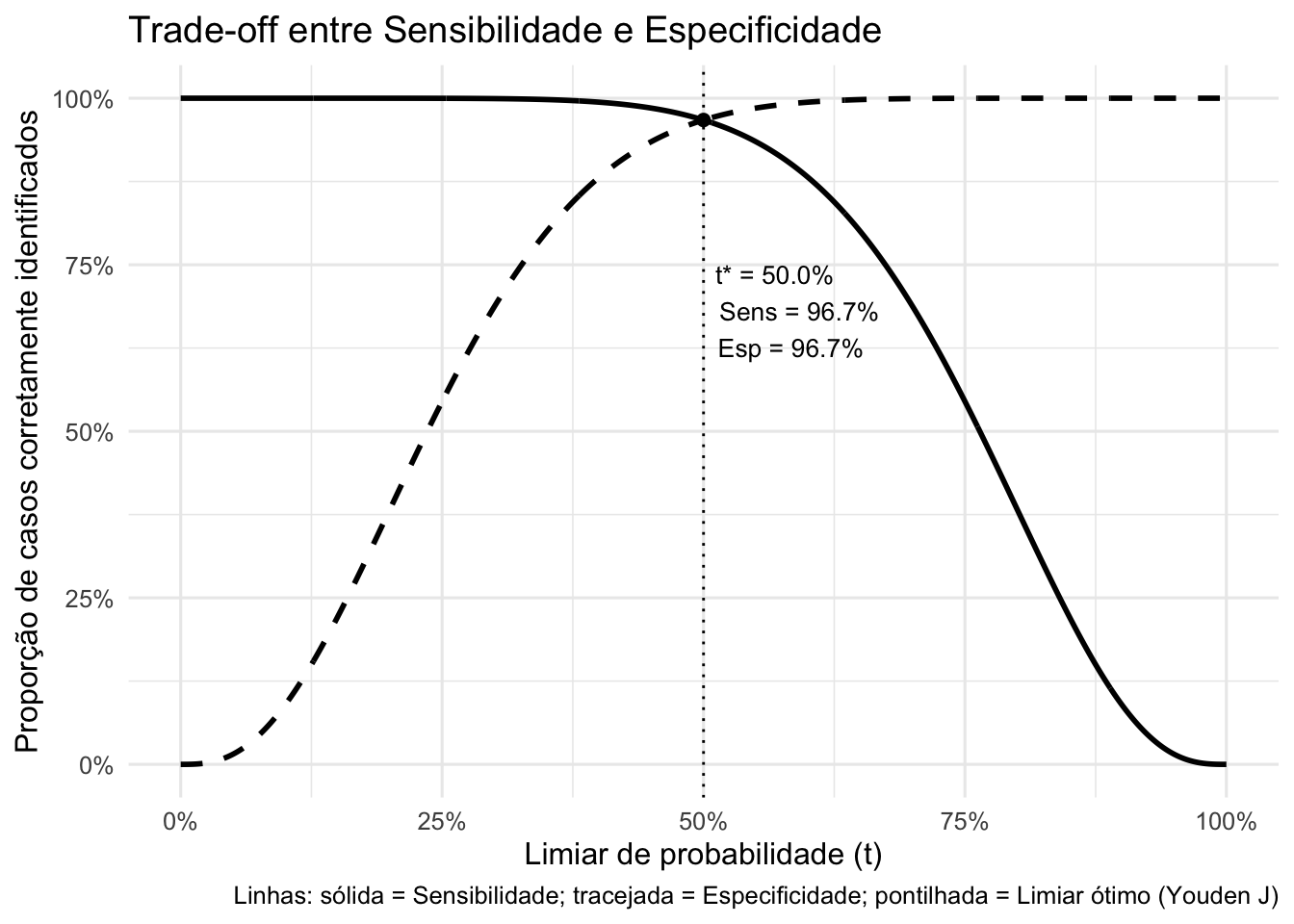
Figura 51.2: Trade-off entre sensibilidade e especificidade em função do limiar de probabilidade (t) para um modelo de classificação.

• Valor preditivo positivo (\(VPP\)) (51.3): Proporção de casos corretamente identificados como verdadeiro-positivos.³⁹⁹

\[\begin{equation} \tag{51.3} VPP = \dfrac{VP}{VP+FP} \end{equation}\]

• Valor preditivo negativo (\(VPN\)) (51.4): Proporção de controles corretamente identificados como verdadeiro-negativos.³⁹⁹

\[\begin{equation} \tag{51.4} VPN = \dfrac{VN}{VN+FN} \end{equation}\]

• Razão de verossimilhança positiva (\(LR+\)) (51.5): Quantifica o quanto a probabilidade de a condição estar presente aumenta quando o teste é positivo.^REF?

\[\begin{equation} \tag{51.5} LR+ = \dfrac{SEN}{1 - ESP} = \dfrac{VP/(VP+FN)}{FP/(FP+VN)} \end{equation}\]

• Razão de verossimilhança negativa (\(LR-\)) (51.6): Quantifica o quanto a probabilidade de a condição estar presente diminui quando o teste é negativo.^REF?

\[\begin{equation} \tag{51.6} LR- = \dfrac{1 - SEN}{ESP} = \dfrac{FN/(VP+FN)}{VN/(FP+VN)} \end{equation}\]

• Acurácia (\(ACU\)), (51.7): Proporção de casos e controles corretamente identificados.³⁹⁹

\[\begin{equation} \tag{51.7} ACU = \dfrac{VP+VN}{VP+VN+FP+FN} \end{equation}\]

• Razão de chances diagnóstica (\(DOR\)) (51.8), (51.9) e (51.10): Razão entre a chance de um teste ser positivo quando a condição está presente e a chance de um teste ser positivo quando a condição está ausente.⁴⁰¹

\[\begin{equation} \tag{51.8} DOR = \dfrac{VP}{FN} \div \dfrac{FP}{VN} = \dfrac{VP \cdot VN}{FP \cdot FN} \end{equation}\]

\[\begin{equation} \tag{51.9} DOR = \dfrac{SEN/(1-SEN)}{(1-ESP)/ESP} = \dfrac{SEN \cdot ESP}{(1-SEN) \cdot (1-ESP)} \end{equation}\]

\[\begin{equation} \tag{51.10} DOR = \dfrac{LR+}{LR-} \end{equation}\]

Tabela 51.2: Probabilidades calculados a partir da tabela de confusão 2x2 para análise de desempenho diagnóstico de testes e variáveis dicotômicas.

	Condição presente	Condição ausente	Total	Probabilidades
Teste positivo	\(VP\)	\(FP\)	\(VP+FP\)	\(VPP = \frac{VP}{VP+FP}\)
Teste negativo	\(FN\)	\(VN\)	\(FN+VN\)	\(VPN = \frac{VN}{VN+FN}\)
Total	\(VP+FN\)	\(FP+VN\)	\(N=VP+VN+FP+FN\)
Probabilidades	\(SEN = \frac{VP}{VP+FN}\)	\(ESP = \frac{VN}{VN+FP}\)		\(ACU = \frac{VP+VN}{VP+VN+FP+FN}\)  \(DOR = \frac{VP \cdot VN}{FP \cdot FN}\)

O pacote riskyr⁴⁰⁰ fornece a função comp_prob para estimar 13 probabilidades relacionadas ao desempenho diagnóstico em tabelas 2x2.

O pacote caret⁴⁰² fornece a função confusionMatrix para estimar 11 probabilidades relacionadas ao desempenho diagnóstico em tabelas 2x2.

51.3 Tabelas 2x3

51.3.1 O que é uma tabela de confusão 2x3?

• É a extensão da tabela 2×2 que inclui uma terceira decisão (deferimento/boundary) além de aceitar (positivo) e rejeitar (negativo).⁴⁰³

• As colunas** representam as decisões** (\(POS\), \(BND\), \(NEG\)) e as linhas representam a verdade de referência (condição presente vs ausente).⁴⁰³

• Essa formulação vem do arcabouço de Three-Way Decisions (3WD), que particiona o universo em três regiões por dois limiares \(\alpha\) e \(\beta\).⁴⁰³

51.3.2 Como as regiões POS, BND e NEG são definidas?

• Dado um escore ou probabilidade condicional \(Pr(C\mid[x])\) para a classe \(C\), classifica-se como \(POS\) (aceitar) quando \(Pr(C\mid[x]) \ge \alpha\), como \(BND\) (deferir) quando \(\beta < Pr(C\mid[x]) < \alpha\) e como \(NEG\) (rejeitar) quando \(Pr(C\mid[x]) \le \beta\), sendo que os limiares \((\alpha,\beta)\) determinam simultaneamente as três regiões e os trade-offs entre acurácia e comprometimento.⁴⁰³

51.3.3 Qual é o formato de uma tabela 2×3?

• Estrutura geral (linhas = condição real; colunas = decisão):

Tabela 51.3: Tabela de confusão 3-vias (2×3) com totais: referência vs decisão (3WD).

	POS (aceitar)	BND (deferir)	NEG (rejeitar)	Total
Condição presente (C)	\(|POS\cap C|\)	\(|BND\cap C|\)	\(|NEG\cap C|\)	\(|POS\cap C|+|BND\cap C|+|NEG\cap C|\)
Condição ausente (\(C^c\))	\(|POS\cap C^c|\)	\(|BND\cap C^c|\)	\(|NEG\cap C^c|\)	\(|POS\cap C^c|+|BND\cap C^c|+|NEG\cap C^c|\)
Total	\(|POS\cap C|+|POS\cap C^c|\)	\(|BND\cap C|+|BND\cap C^c|\)	\(|NEG\cap C|+|NEG\cap C^c|\)	\(N\)

51.3.4 Quais são as medidas básicas na 2×3?

• Acurácia em POS (\(M_{PT}\)), equação (51.11): Proporção de positivos corretamente identificados na região POS.⁴⁰³

\[\begin{equation} \tag{51.11} M_{PT} = \dfrac{|POS \cap C|}{|POS|} \end{equation}\]

• Erro em POS (\(M_{PF}\)), equação (51.12): Proporção de negativos incorretamente classificados na região POS.⁴⁰³

\[\begin{equation} \tag{51.12} M_{PF} = \dfrac{|POS \cap C^{c}|}{|POS|} \end{equation}\]

• Acurácia em NEG (\(M_{NF}\)), equação (51.13): Proporção de negativos corretamente identificados na região NEG.⁴⁰³

\[\begin{equation} \tag{51.13} M_{NF} = \dfrac{|NEG \cap C^{c}|}{|NEG|} \end{equation}\]

• Erro em NEG (\(M_{NT}\)), equação (51.14): Proporção de positivos incorretamente classificados na região NEG.⁴⁰³

\[\begin{equation} \tag{51.14} M_{NT} = \dfrac{|NEG \cap C|}{|NEG|} \end{equation}\]

• Frações em BND (\(M_{BT}\) e \(M_{BF}\)), equações (51.15) e (51.16): Proporção de deferimentos verdadeiros e falsos.⁴⁰³

\[\begin{equation} \tag{51.15} M_{BT} = \dfrac{|BND \cap C|}{|BND|} \end{equation}\] \[\begin{equation} \tag{51.16} M_{BF} = \dfrac{|BND \cap C^{c}|}{|BND|} \end{equation}\]

51.3.5 Como escolher os limiares \(\alpha\) e \(\beta\)?

• Os limiares \((\alpha,\beta)\) controlam o tamanho das regiões \(POS\), \(NEG\) e \(BND\) e, portanto, os trade-offs entre “acertar mais” (acurácia nas regiões) e “decidir mais” (comprometimento; menos deferimentos).⁴⁰³

51.3.6 Quando preferir 3-vias em vez de 2×2?

• Quando o custo de erro é assimétrico e/ou há incerteza relevante.⁴⁰³

• O deferimento (\(BND\)) evita decisões precipitadas e permite avaliação adicional, equilibrando acurácia e cobertura.⁴⁰³

• É particularmente útil em triagens diagnósticas com etapas confirmatórias.⁴⁰³

51.4 Curvas ROC

51.4.1 O que representa a curva ROC?

• A relação entre sensibilidade (\(SEN\)) no eixo vertical e \(1 - ESP\) no eixo horizontal.⁴⁰⁴

• Cada ponto na curva corresponde a um ponto de corte possível do teste.⁴⁰⁴

51.4.2 Quais são os tipos de curva ROC?

• Curva empírica: conecta diretamente os pontos obtidos a partir dos diferentes pontos de corte observados.⁴⁰⁵

• Curva suavizada (paramétrica): assume uma distribuição binormal e gera uma curva ajustada por máxima verossimilhança.⁴⁰⁵

51.4.3 Como definir o melhor ponto de corte?

• O ponto de corte em uma curva ROC representa um balanço entre sensibilidade e especificidade, ou seja, a taxa de verdadeiros positivos e a taxa de falsos positivos.^404,405

• O método de Youden (equação (51.17) maximiza a diferença entre a taxa de verdadeiros positivos e a taxa de falsos positivos. O ponto de corte ideal será aquele com maior valor de \(Y\).¹²⁹

\[\begin{equation} \tag{51.17} Y = SEN + ESP - 1 \end{equation}\]

• O método da distância Euclidiana ((51.18) minimiza a distância entre um ponto da curva ROC e o ponto (0,1), que representa sensibilidade perfeita (\(SEN = 100%\)) e especificidade perfeita (\(ESP = 100%\)). O ponto de corte ideal será aquele com menor valor de \(D\).⁴⁰⁶

\[\begin{equation} \tag{51.18} D = \sqrt{(1 - SEN)^2 + (1 - ESP)^2} \end{equation}\]

51.4.4 O que é a área sob a curva (AUROC)?

• A área sob a curva ROC (AUC ou AUROC) quantifica o poder de discriminação ou desempenho diagnóstico na classificação de uma variável dicotômica.⁴⁰⁷

• A área sob a curva (\(AUC\)) resume o desempenho global e representa a probabilidade de o teste classificar corretamente um caso positivo selecionado aleatoriamente em relação a um caso negativo selecionado aleatoriamente.⁴⁰⁴

51.4.5 Como calcular a AUC?

• Método não paramétrico: soma das áreas trapezoidais sob a curva empírica (51.19). Pode subestimar AUC quando os dados são discretos.⁴⁰⁵

\[\begin{equation} \tag{51.19} AUC = \sum_{i=1}^{n-1} (x_{i+1} - x_i) \cdot \dfrac{y_i + y_{i+1}}{2} \end{equation}\]

• Método paramétrico (binormal): mais robusto para dados em escala ordinal, com viés reduzido (51.20), onde\(\Phi\) é a função de distribuição acumulada da Normal padrão, \(\mu_1\) e \(\mu_0\) são as médias dos escores para os grupos positivo e negativo, respectivamente, e \(\sigma_1^2\) e \(\sigma_0^2\) são as variâncias dos escores para os grupos positivo e negativo, respectivamente.⁴⁰⁵

\[\begin{equation} \tag{51.20} AUC = \Phi\left(\dfrac{\mu_1 - \mu_0}{\sqrt{\sigma_1^2 + \sigma_0^2}}\right) \end{equation}\]

• AUC deve sempre vir acompanhada de intervalo de confiança (IC95%).⁴⁰⁵

O pacote proc⁴⁰⁸ fornece a função plot.roc para criar uma curva ROC.

51.4.6 Como interpretar a área sob a curva (ROC)?

• A área sob a curva AUC varia no intervalo \([0.5; 1]\), com valores mais elevados indicando melhor discriminação ou desempenho do modelo de classificação.⁴⁰⁷

• As interpretações qualitativas (isto é: pobre/fraca/baixa, moderada/razoável/aceitável, boa ou muito boa/alta/excelente) dos valores de área sob a curva são arbitrários e não devem ser considerados isoladamente.⁴⁰⁷

• Modelos de classificação com valores altos de área sob a curva podem ser enganosos se os valores preditos por esses modelos não estiverem adequadamente calibrados.⁴⁰⁷

• Diferenças pequenas entre AUCs podem não ser estatisticamente significativas.⁴⁰⁴

• A interpretação clínica pode ser equivocada se não houver teste estatístico adequado.⁴⁰⁴

• Se as curvas vêm do mesmo conjunto de pacientes, aplique o teste de DeLong.⁴⁰⁴

• Se as curvas vêm de amostras independentes, use métodos como Dorfman-Alf.⁴⁰⁴

51.4.7 Por que uma AUC menor que 0.5 está errada?

• Porque indica desempenho pior que o acaso.⁴⁰⁴

• Geralmente decorre de seleção incorreta da direção do teste ou da variável de estado.⁴⁰⁴

• Verifique se o software está configurado para maiores valores indicam presença do evento ou o inverso.⁴⁰⁴

• Ajuste a direção do teste para que \(AUC \geq 0.5\).⁴⁰⁴

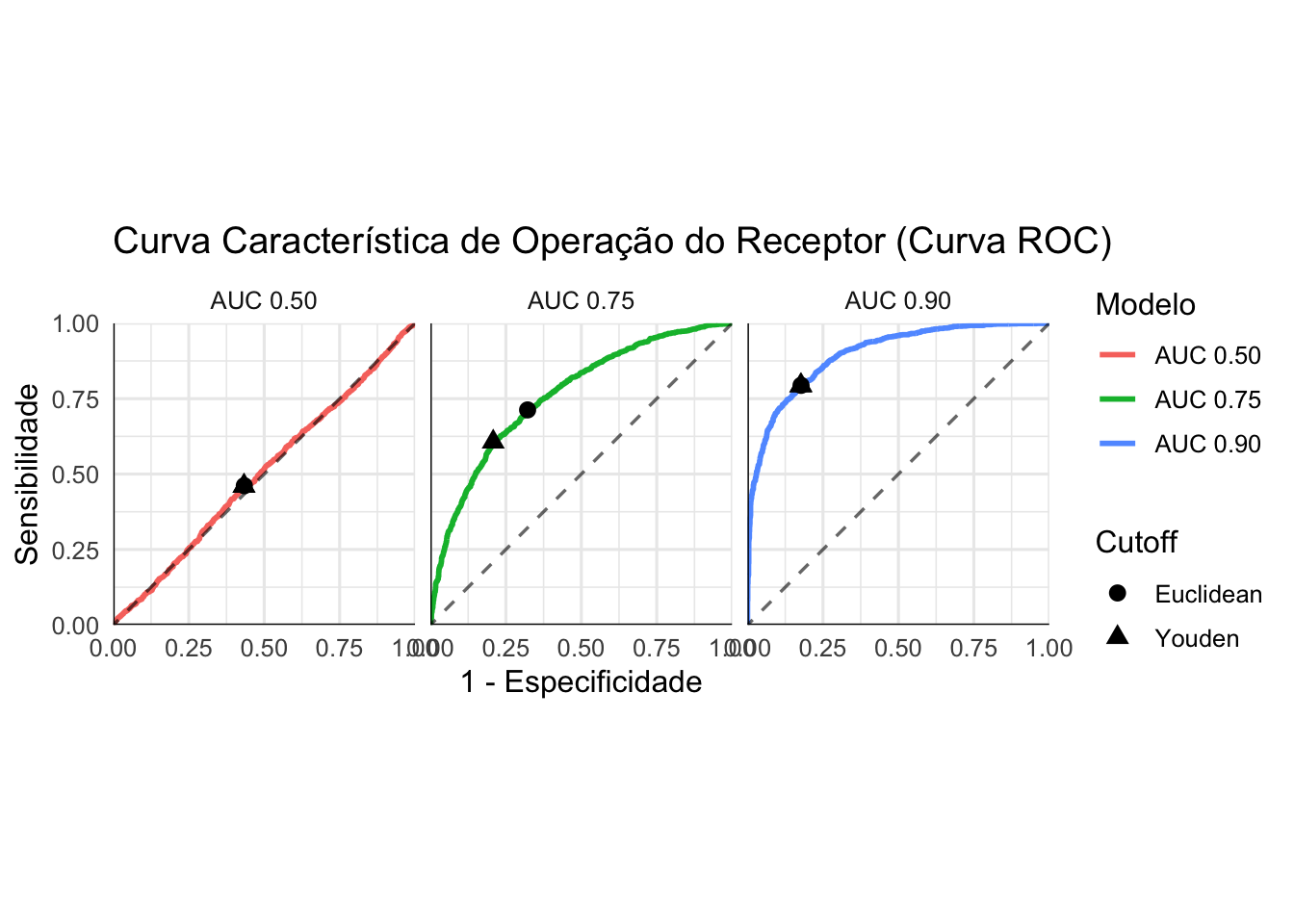
Figura 51.3: Curva ROC (Receiver Operating Characteristic) para um modelos de classificação com diferentes desempenhos diagnósticos.

51.4.8 Como analisar o desempenho diagnóstico em desfechos com distribuição trimodal na população?

• Limiares duplos podem ser utilizados para análise de desempenho diagnóstico de testes com distribuição trimodal.⁴⁰⁹

51.5 Gráficos de cruzes

51.5.1 O que um gráfico de cruzes (crosshair)?

• .⁴¹⁰

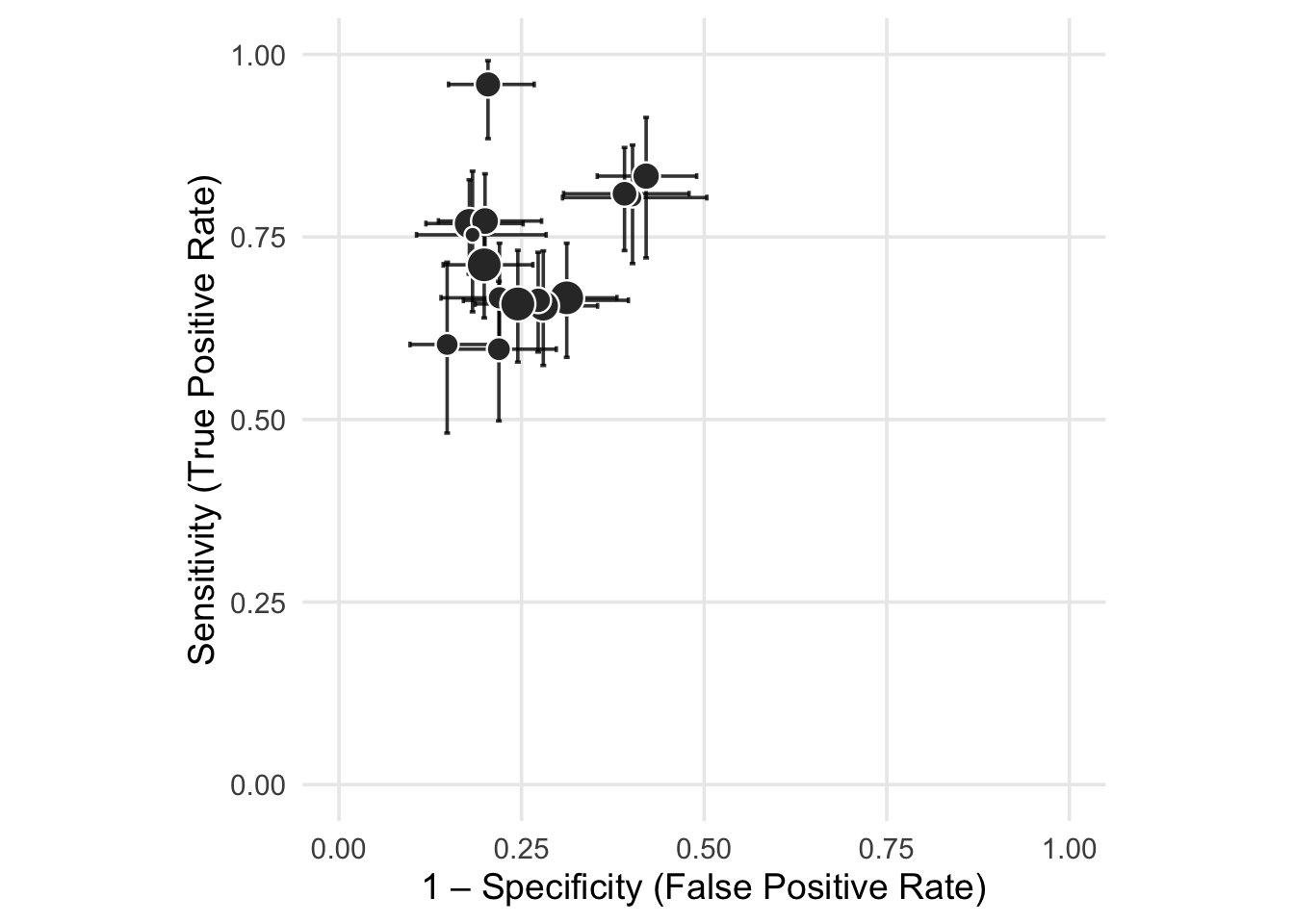
Figura 51.4: Gráfico de cruzes (crosshair) em espaço ROC (Receiver Operating Characteristic) para 15 estudos simulados de desempenho diagnóstico.

O pacote mada⁴¹¹ fornece a função crosshair para criar um gráfico crosshair⁴¹⁰ a partir de dados de verdadeiro-positivo, falso-positivo, verdadeiro-negativo e verdadeiro-positivo de tabelas de confusão 2x2.

51.6 Interpretação da validade de um teste

51.6.1 Que itens devem ser verificados na interpretação de um estudo de validade?

• O novo teste foi comparado junto ao método padrão-ouro.³⁹⁹

• As probabilidades pontuais estimadas que caracterizam o desempenho diagnóstico do novo teste são altas e adequadas para sua aplicação clínica.³⁹⁹

• Os intervalos de confiança estimados para as probabilidades do novo teste são estreitos e adequadas para sua aplicação clínica.³⁹⁹

• O novo teste possui adequada confiabilidade intra/inter examinadores.³⁹⁹

• O estudo de validação incluiu um espectro adequado da amostra.³⁹⁹

• Todos os participantes realizaram ambos o novo teste e o padrão-ouro no estudo de validação.³⁹⁹

• Os examinadores do novo teste estavam cegados para o resultado do teste padrão-ouro.³⁹⁹

51.7 Diretrizes para redação

51.7.1 Quais são as diretrizes para redação de estudos diagnósticos?

• Visite a rede Enhancing the QUAlity and Transparency Of health Research (EQUATOR Network) para encontrar diretrizes específicas.

• STARD 2015: An Updated List of Essential Items for Reporting Diagnostic Accuracy Studies:⁴¹² https://www.equator-network.org/reporting-guidelines/stard/

Citar como:
Ferreira, Arthur de Sá. Ciência com R: Perguntas e respostas para pesquisadores e analistas de dados. Rio de Janeiro: 1a edição,

Referências

129.

Youden WJ. Index for rating diagnostic tests. Cancer. 1950;3(1):32–35. doi:10.1002/1097-0142(1950)3:1<32::aid-cncr2820030106>3.0.co;2-3

398.

Steckelberg A, Balgenorth A, Berger J, Mühlhauser I. Explaining computation of predictive values: 2 × 2 table versus frequency tree. A randomized controlled trial [ISRCTN74278823]. BMC Medical Education. 2004;4(1). doi:10.1186/1472-6920-4-13

399.

Greenhalgh T. How to read a paper: Papers that report diagnostic or screening tests. BMJ. 1997;315(7107):540–543. doi:10.1136/bmj.315.7107.540

400.

Neth H, Gaisbauer F, Gradwohl N, Gaissmaier W. riskyr: Rendering Risk Literacy more Transparent.; 2022. https://CRAN.R-project.org/package=riskyr.

401.

Glas AS, Lijmer JG, Prins MH, Bonsel GJ, Bossuyt PMM. The diagnostic odds ratio: a single indicator of test performance. Journal of Clinical Epidemiology. 2003;56(11):1129–1135. doi:10.1016/s0895-4356(03)00177-x

402.

Kuhn, Max. Building Predictive Models in R Using the caret Package. Journal of Statistical Software. 2008;28(5):1–26. doi:10.18637/jss.v028.i05

403.

Xu J, Zhang Y, Miao D. Three-way confusion matrix for classification: A measure driven view. Information Sciences. 2020;507:772–794. doi:10.1016/j.ins.2019.06.064

404.

He Z, Zhang Q, Song M, Tan X, Wang W. Four overlooked errors in ROC analysis: how to prevent and avoid. BMJ Evidence-Based Medicine. 2024;30(3):208–211. doi:10.1136/bmjebm-2024-113078

405.

Park SH, Goo JM, Jo CH. Receiver Operating Characteristic (ROC) Curve: Practical Review for Radiologists. Korean Journal of Radiology. 2004;5(1):11. doi:10.3348/kjr.2004.5.1.11

406.

Park SH, Goo JM, Jo CH. UniODA vs ROC Analysis: Computing the “optimal” cut-point. Optimal Data Analysis. 2014;3(14):117–120. https://odajournal.com/wp-content/uploads/2019/01/v3a29.pdf.

407.

Hond AAH de, Steyerberg EW, Calster B van. Interpreting area under the receiver operating characteristic curve. The Lancet Digital Health. 2022;4(12):e853–e855. doi:10.1016/s2589-7500(22)00188-1

408.

Robin X, Turck N, Hainard A, et al. pROC: an open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinformatics. 2011;12:77. doi:10.1186/1471-2105-12-77

409.

Ferreira ADS, Meziat-Filho N, Ferreira APA. Double threshold receiver operating characteristic plot for three-modal continuous predictors. Computational Statistics. 2021;36(3):2231–2245. doi:10.1007/s00180-021-01080-9

410.

Phillips B, Stewart LA, Sutton AJ. ‘Cross hairs’ plots for diagnostic meta-analysis. Research Synthesis Methods. 2010;1(3-4):308–315. doi:10.1002/jrsm.26

411.

Sousa-Pinto PD with contributions from B. mada: Meta-Analysis of Diagnostic Accuracy.; 2022. https://CRAN.R-project.org/package=mada.

412.

Bossuyt PM, Reitsma JB, Bruns DE, et al. STARD 2015: an updated list of essential items for reporting diagnostic accuracy studies. BMJ. outubro 2015:h5527. doi:10.1136/bmj.h5527