Capítulo 30 Regressão

30.1 Análise de regressão

30.1.1 O que é regressão?

• Regressão refere-se a uma equação matemática que permite que uma ou mais variável(is) de desfecho (dependentes) seja(m) prevista(s) a partir de uma ou mais variável(is) independente(s). A regressão implica em uma direção de efeito, mas não garante causalidade.²⁵¹

• Para estimar os efeitos imparciais de um fator de exposição primária sobre uma variável de desfecho, frequentemente constroem-se modelos estatísticos de regressão.¹⁹⁹

O pacote modelsummary²⁸⁵ fornece as funções modelsummary e modelplot para gerar tabelas e gráficos de coeficientes de regressão.

O pacote gtsummary¹⁹² fornece a função tbl_regression para construção da ‘Tabela 2’ com dados do modelo de regressão.

30.1.2 Quais são os algoritmos de regressão?

• Linear: Simples, Múltipla, Polinomial.^REF?

• Linear generalizado: Binomial (logística), Multinomial, Ordinal, Poisson, Binomial negativa, Gama.^REF?

• Não-linear (nos parâmetros).^REF?

• Aditivo generalizado.^REF?

• Efeitos mistos: Linear, Generalizado.^REF?

• Sobrevida: Cox, Weibull, Exponencial, Log-normal, Log-logístico.^REF?

• Regularização: Ridge, Lasso.^REF?

30.2 Estruturas de análise de regressão

30.2.1 O que são análises de regressão simples?

• A análise de regressão simples consiste em modelos estatísticos com 1 variável dependente (desfecho) e 1 variável independente (preditor).²⁸⁶

• A equação de regressão simples é expressa como (30.1), onde \(Y\) é a variável dependente, \(X\) é a variável independente, \(\beta_0\) é o intercepto (constante), \(\beta_1\) é o coeficiente de regressão da variável independente e \(\epsilon\) representa o erro aleatório do modelo.²⁸⁶

\[\begin{equation} \tag{30.1} Y = \beta_0 + \beta_1 X + \epsilon \end{equation}\]

30.2.2 O que são análises de regressão multivariável?

• A análise multivariável (ou múltiplo) consiste em modelos estatísticos com 1 variável dependente (desfecho) e duas ou mais variáveis independentes.²⁸⁶

• A equação de regressão multivariável é expressa como (30.2), onde \(Y\) é a variável dependente, \(X_1, X_2, ..., X_n\) são as variáveis independentes, \(\beta_0\) é o intercepto (constante), \(\beta_1, \beta_2, ..., \beta_n\) são os coeficientes de regressão das variáveis independentes e \(\epsilon\) representa o erro aleatório do modelo.²⁸⁶

\[\begin{equation} \tag{30.2} Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + ... + \beta_n X_n + \epsilon \end{equation}\]

30.2.3 O que são análises de regressão multivariada?

• A análise multivariada consiste em modelos estatísticos com 2 ou mais variáveis dependente (desfechos) e duas ou mais variáveis independentes.²⁸⁶

• A equação de regressão multivariada é expressa como (30.3), onde \(Y_1, Y_2, ..., Y_m\) são as variáveis dependentes, \(X_1, X_2, ..., X_n\) são as variáveis independentes, \(\beta_{0j}\) é o intercepto (constante) da variável dependente \(Y_j\), \(\beta_{ij}\) são os coeficientes de regressão das variáveis independentes para a variável dependente \(Y_j\) e \(\epsilon_j\) representa o erro aleatório do modelo para a variável dependente \(Y_j\).²⁸⁶

\[\begin{align} \tag{30.3} Y_1 &= \beta_{01} + \beta_{11} X_1 + \beta_{12} X_2 + \dots + \beta_{1n} X_n + \epsilon_1 \\ Y_2 &= \beta_{02} + \beta_{21} X_1 + \beta_{22} X_2 + \dots + \beta_{2n} X_n + \epsilon_2 \\ &\vdots \\ Y_m &= \beta_{0m} + \beta_{m1} X_1 + \beta_{m2} X_2 + \dots + \beta_{mn} X_n + \epsilon_m \end{align}\]

30.3 Tipos e famílias de modelos de regressão

30.3.1 O que são modelos de regressão linear?

• Modelos lineares (equação (30.4)) descrevem uma relação linear nos parâmetros entre um desfecho contínuo \(Y\) e um ou mais preditores \(X\).^REF?

• Assumem erros independentes, de média zero e variância constante (homocedasticidade).^REF?

• A normalidade dos resíduos é uma hipótese comum para inferência estatística, mas não obrigatória para estimação dos coeficientes.^REF?

\[\begin{equation} \tag{30.4} Y = \beta_0 + \sum_{i=1}^{n} \beta_i X_i + \epsilon \end{equation}\]

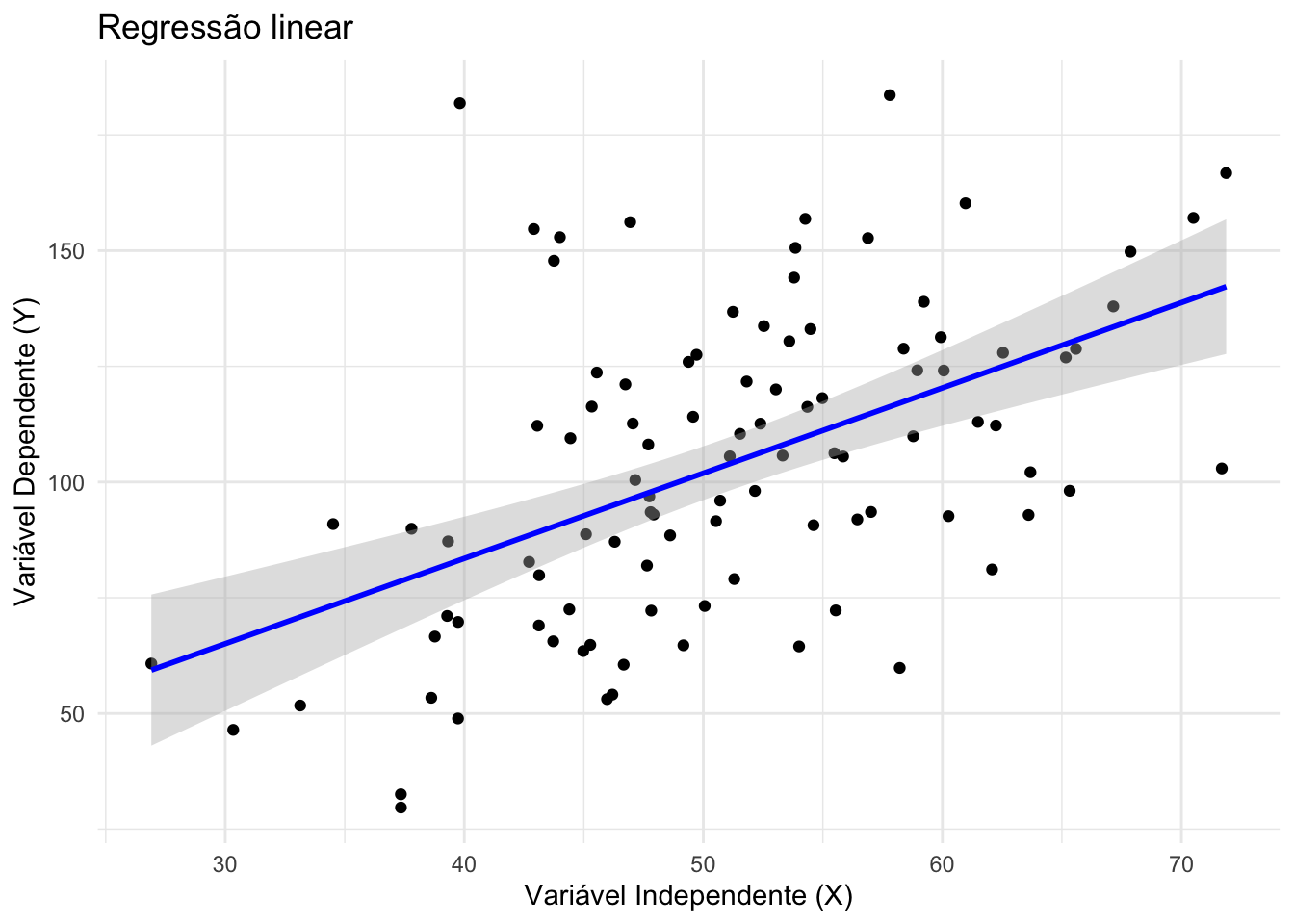
Figura 30.1: Regressão linear.

30.3.2 O que são modelos de regressão polinomial?

• São extensões da regressão linear em que se incluem termos elevados a potências das variáveis independentes (ex.: \(X^2\), \(X^3\)), permitindo capturar relações curvas.^REF?

• Modelos de regressão polinomial continuam sendo lineares nos parâmetros, por isso ainda se enquadram como um caso particular da regressão linear.^REF?

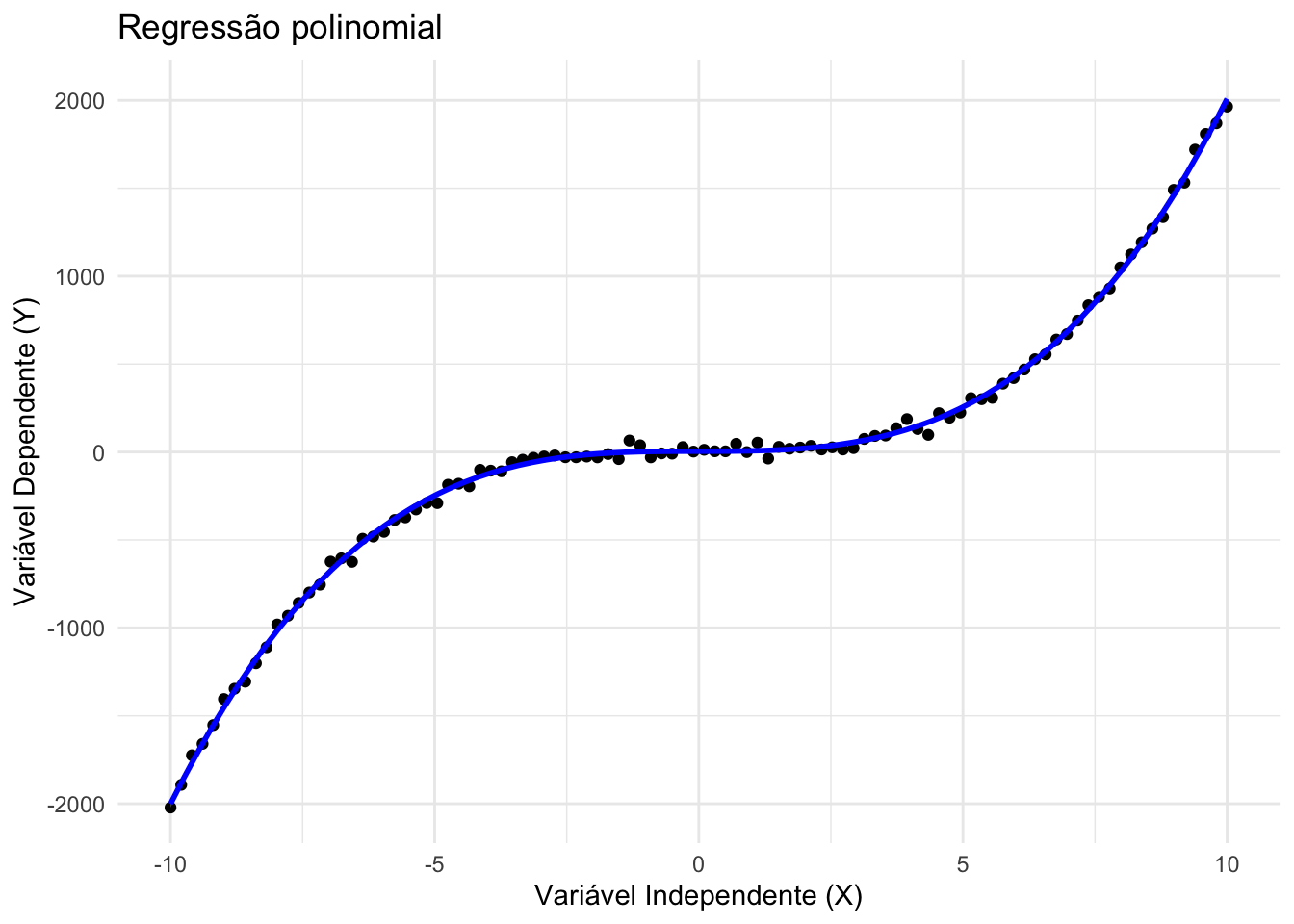
Figura 30.2: Regressão polinomial.

30.3.3 O que são modelos de regressão não-linear?

• São modelos em que a relação entre os parâmetros e a variável resposta não é linear.

• Podem assumir formas funcionais mais complexas (ex.: exponencial, logarítmica, logística).^REF?

• Importante diferenciar “não-linear na variável” (ex.: polinomial) de “não-linear no parâmetro” (ex.: modelos logísticos de crescimento).^REF?

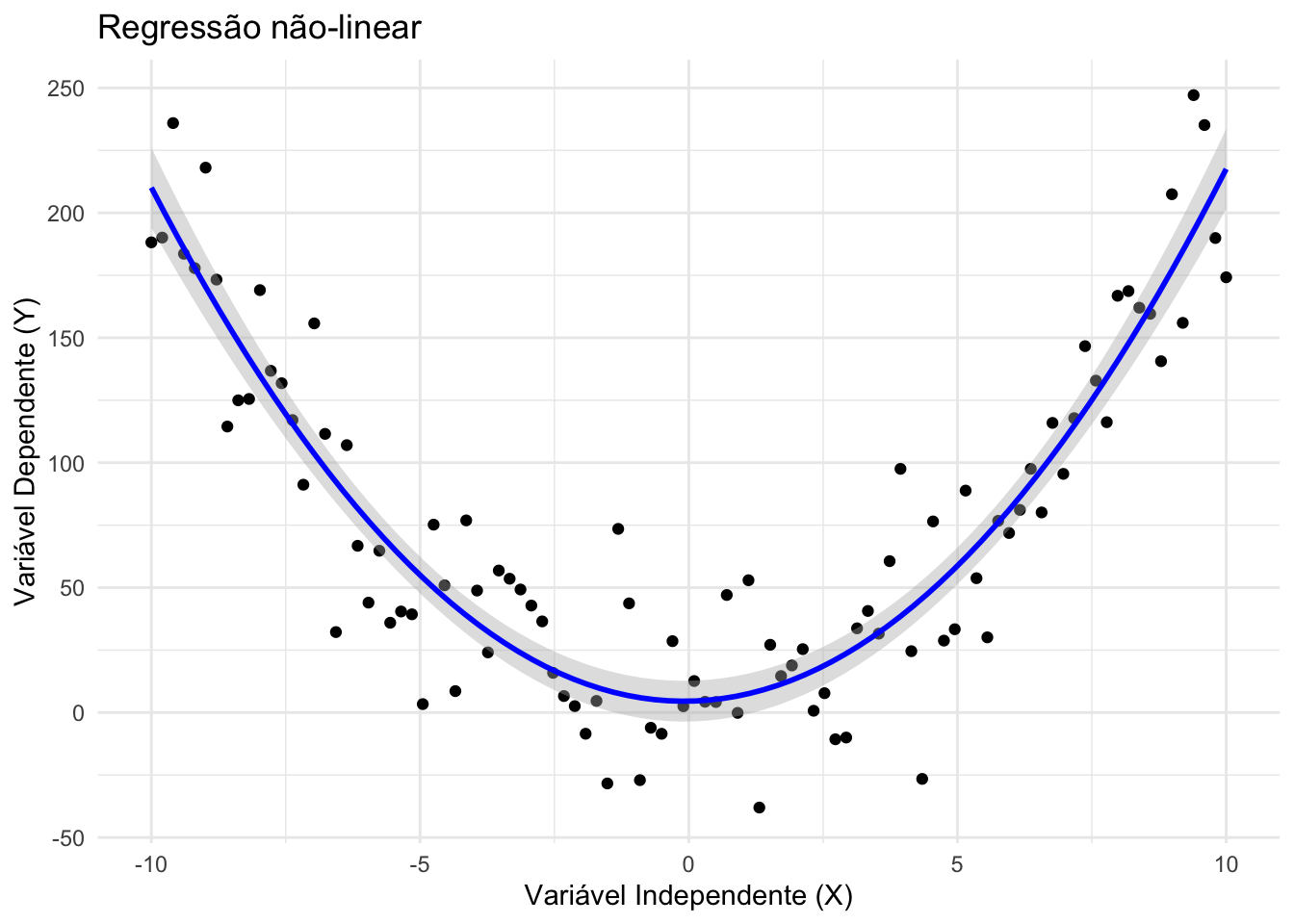
Figura 30.3: Regressão não-linear.

30.3.4 O que são modelos de regressão logística?

• Modelos logísticos são casos de regressão linear generalizada em que a resposta \(Y\) é binária.^REF?

• A equação (30.5) modela a razão de chances (odds) em função dos preditores.^REF?

• A ligação (link) usada é o logit.^REF?

\[\begin{equation} \tag{30.5} \log\left(\frac{p}{1-p}\right) = \beta_0 + \beta_1 X + ... + \beta_n X_n \end{equation}\]

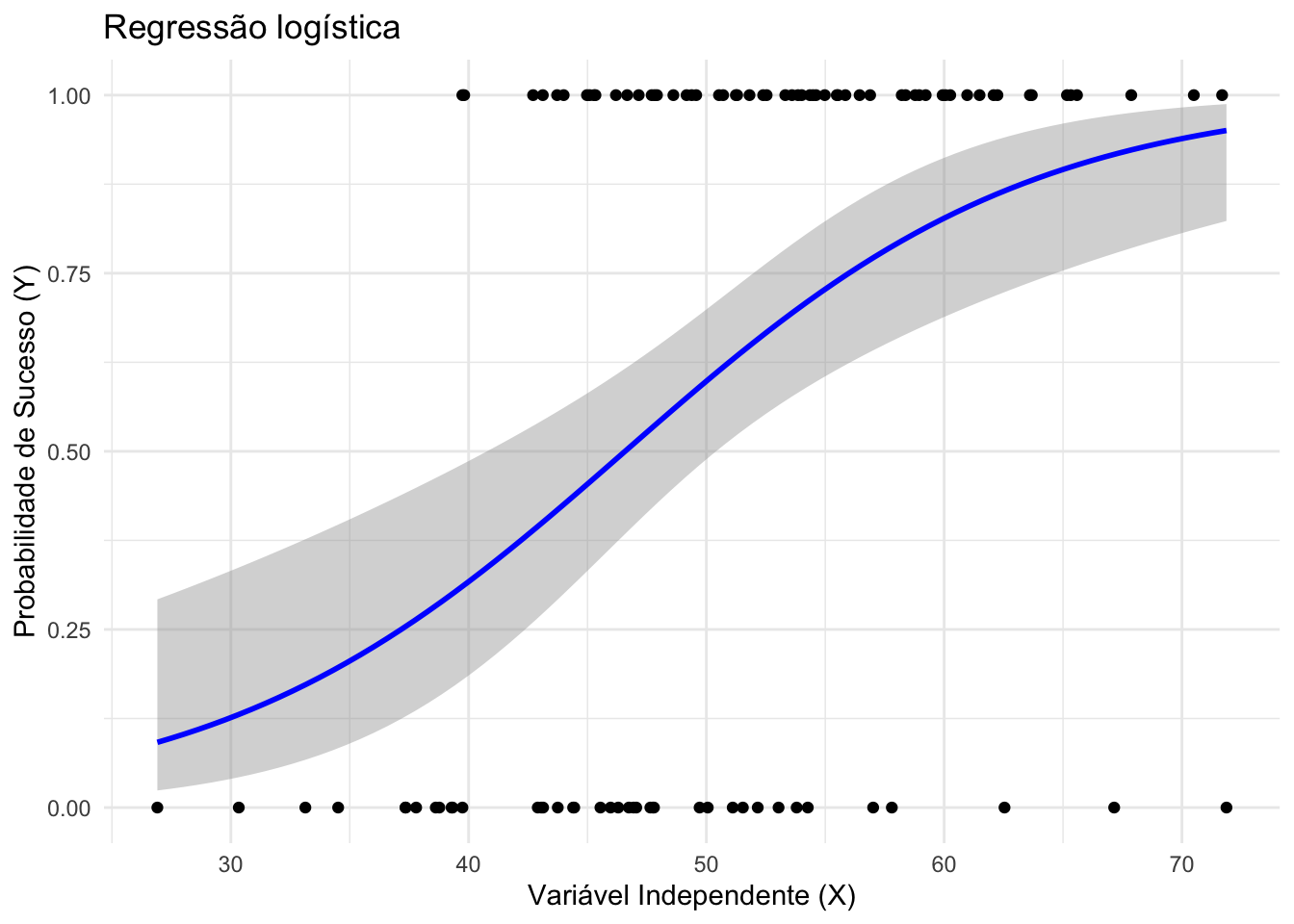
Figura 30.4: Regressão logística.

30.3.5 O que são modelos de regressão multinomial?

• Modelos de regressão multinomial são usados quando a variável resposta é categórica com mais de dois níveis não ordenados.^REF?

• Estendem a regressão logística binária, modelando as razões de chances (odds ratios) de cada categoria em relação a uma categoria de referência.^REF?

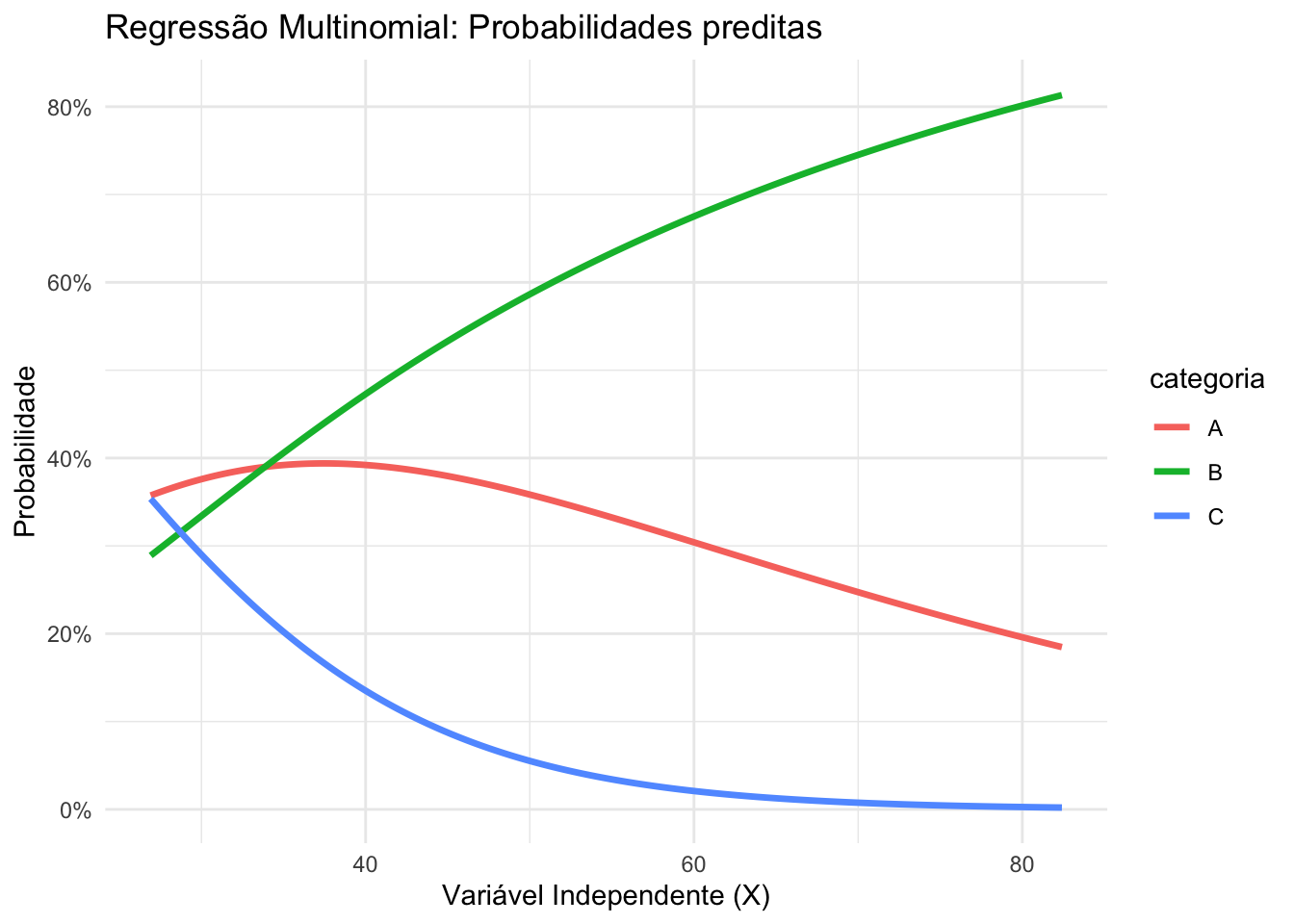
Figura 30.5: Regressão multinomial

30.3.6 O que são modelos de regressão ordinal?

• Modelos de regressão ordinal são usados quando a variável resposta é categórica com mais de dois níveis ordenados.^REF?

• Modelam a probabilidade acumulada de estar em ou abaixo de cada categoria, usando uma função de ligação logit, probit ou log-log.^REF?

• Assumem a proporcionalidade dos coeficientes entre as categorias (proportional odds).^REF?

30.3.7 O que são modelos de regressão de Poisson?

• Modelos de regressão de Poisson são usados quando a variável resposta é uma contagem de eventos não negativos.^REF?

• Assumem que \(Y \sim Poisson(\mu)\), com \(\mu = E[Y|X]\) relacionado aos preditores via função de ligação log.^REF?

• A sobre-dispersão (variância maior que a média) pode exigir modelos alternativos como a regressão binomial negativa.^REF?

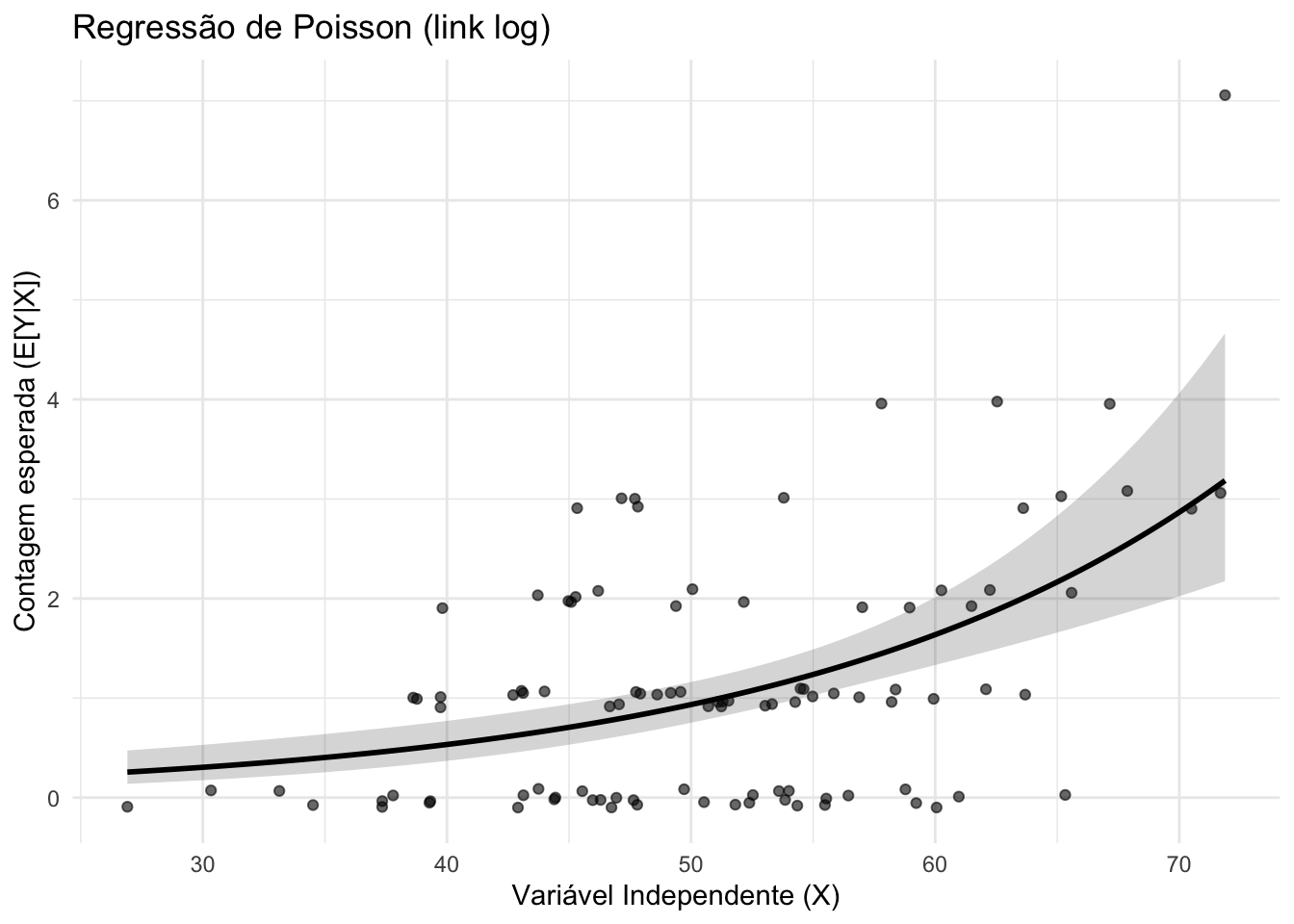
Figura 30.6: Regressão de Poisson.

30.3.8 O que são modelos de regressão binomial negativa?

• Modelos de regressão binomial negativa são usados para contagens superdispersas, onde a variância excede a média.^REF?

• Introduzem um parâmetro de dispersão adicional para modelar a variabilidade extra.^REF?

• A função de ligação log é comumente usada, semelhante à regressão de Poisson.^REF?

30.3.9 O que são modelos de regressão Gama?

• Modelos de regressão Gama são usados para variáveis resposta contínuas e positivas, frequentemente com distribuição assimétrica.^REF?

• A função de ligação log é comumente usada para garantir predições positivas.^REF?

30.3.10 O que são modelos de regressão com efeitos mistos?

• Modelos de efeitos mistos incorporam efeitos fixos (coeficientes comuns a todos os indivíduos) e efeitos aleatórios (variações específicas de grupos ou indivíduos).^REF?

• Usados para dados hierárquicos ou longitudinais, onde observações estão agrupadas (ex.: pacientes dentro de hospitais).^REF?

• Permitem modelar correlações intra-grupo e variabilidade entre grupos.^REF?

30.3.11 O que são modelos de regressão com efeitos mistos generalizados?

• Modelos de efeitos mistos generalizados (GLMM) estendem os modelos de efeitos mistos para variáveis resposta que seguem distribuições da família exponencial (ex.: binomial, Poisson).^REF?

• Combinam a flexibilidade dos modelos lineares generalizados com a capacidade de modelar correlações e variabilidade entre grupos.^REF?

• Usados para dados hierárquicos ou longitudinais com desfechos não normais.^REF?

30.3.12 O que são modelos de regressão ridge?

• Regressão ridge é um modelo linear regularizado que adiciona uma penalização L2 à soma dos quadrados dos coeficientes.^REF?

• Ajuda a reduzir multicolinearidade e overfitting, encolhendo os coeficientes em direção a zero, mas nunca os tornando exatamente nulos.^REF?

• O hiperparâmetro de regularização é \(\lambda\), controlando a intensidade da penalização. Valores maiores de \(\lambda\) resultam em maior encolhimento dos coeficientes.^REF?

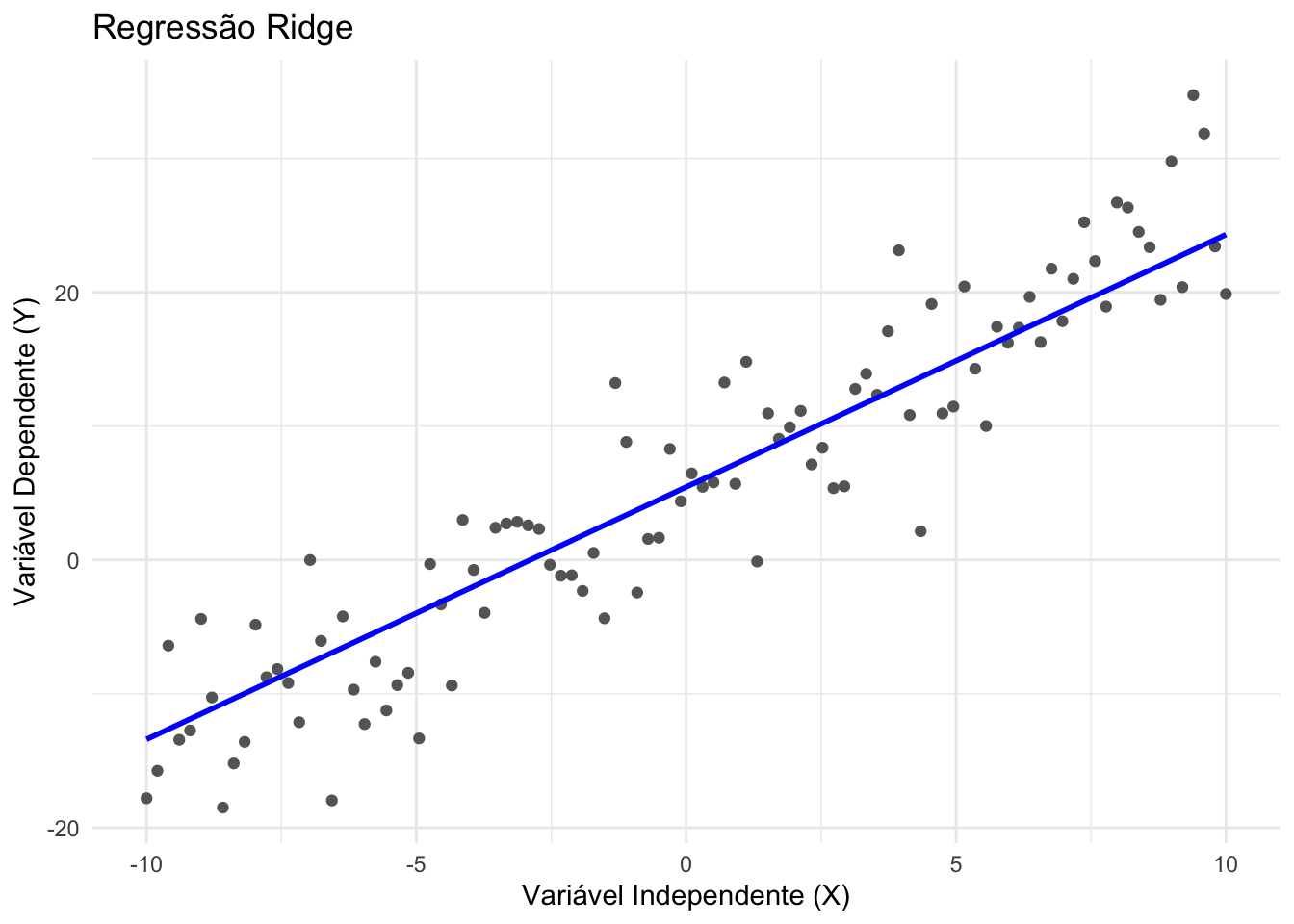
Figura 30.7: Regressão ridge.

30.3.13 O que são modelos de regressão lasso?

• Regressão lasso (Least Absolute Shrinkage and Selection Operator) utiliza penalização L1, que pode zerar coeficientes.^REF?

• Além de reduzir overfitting, também realiza seleção automática de variáveis.^REF?

• Enquanto a regressão ridge mantém todos os preditores, a lasso pode excluir variáveis irrelevantes.^REF?

30.4 Preparação de variáveis

30.4.1 Como preparar as variáveis categóricas para análise de regressão?

• Variáveis fictícias (dummy) compreendem variáveis criadas para introduzir, nos modelos de regressão, informações contidas em outras variáveis que não podem ser medidas em escala numérica.²⁸⁷

• Variáveis categóricas nominais, com 2 ou mais níveis, devem ser subdivididas em variáveis fictícias dicotômicas para ser usada em modelos de regressão.²⁸⁸

• Cada nível da variável categórica nominal será convertido em uma nova variável fictícias dicotômica, tal que a nova variável dicotômica assume valor 1 para a presença do nível correspondente e 0 em qualquer outro caso.²⁸⁸

O pacote fastDummies²⁸⁹ fornece a função dummy_cols para preparar as variáveis categóricas fictícias para análise de regressão.

30.4.2 Por que é comum escolher a categoria mais frequente como referência em modelos epidemiológicos?

• Maior estabilidade estatística: a categoria mais frequente costuma gerar estimativas mais estáveis, com menor erro padrão nos coeficientes das demais categorias.^REF?

• A escolha da referência não altera o ajuste nem o valor predito pelo modelo — apenas muda o ponto de comparação.^REF?

30.5 Multicolinearidade

30.5.1 O que é multicolinearidade?

• Multicolinearidade representa a intercorrelação entre as variáveis independentes (explanatórias) de um modelo.²⁸³

30.5.2 Como diagnosticar multicolinearidade de forma quantitativa?

• Verifique a existência de multicolinearidade entre as variáveis candidatas.²⁹⁰

• O Coeficiente de determinação (\(R^2\)) é uma medida de quão bem as variáveis independentes explicam a variabilidade da variável dependente. Valores próximos a 1 indicam que as variáveis independentes estão fortemente correlacionadas entre si, o que pode indicar multicolinearidade.²⁸³

• O Fator de Inflação da Variância (variance inflation factor, VIF) é uma medida que quantifica o quanto a variância de um coeficiente de regressão é inflacionada devido à multicolinearidade. Valores de VIF maiores que 10 são frequentemente considerados indicativos de multicolinearidade significativa.²⁸³

• O recíproco da VIF é chamado de Tolerância, que mede a proporção da variância de uma variável independente que não é explicada pelas outras variáveis independentes. Valores baixos de Tolerância (geralmente abaixo de 0.1) indicam multicolinearidade.²⁸³

• O número de condições (Condition Number) é uma medida que avalia a estabilidade numérica de um modelo de regressão. Valores altos (entre 10 de 30) indicam multicolinearidade, e valores maiores que 30 indicam forte multicolinearidade.²⁸³

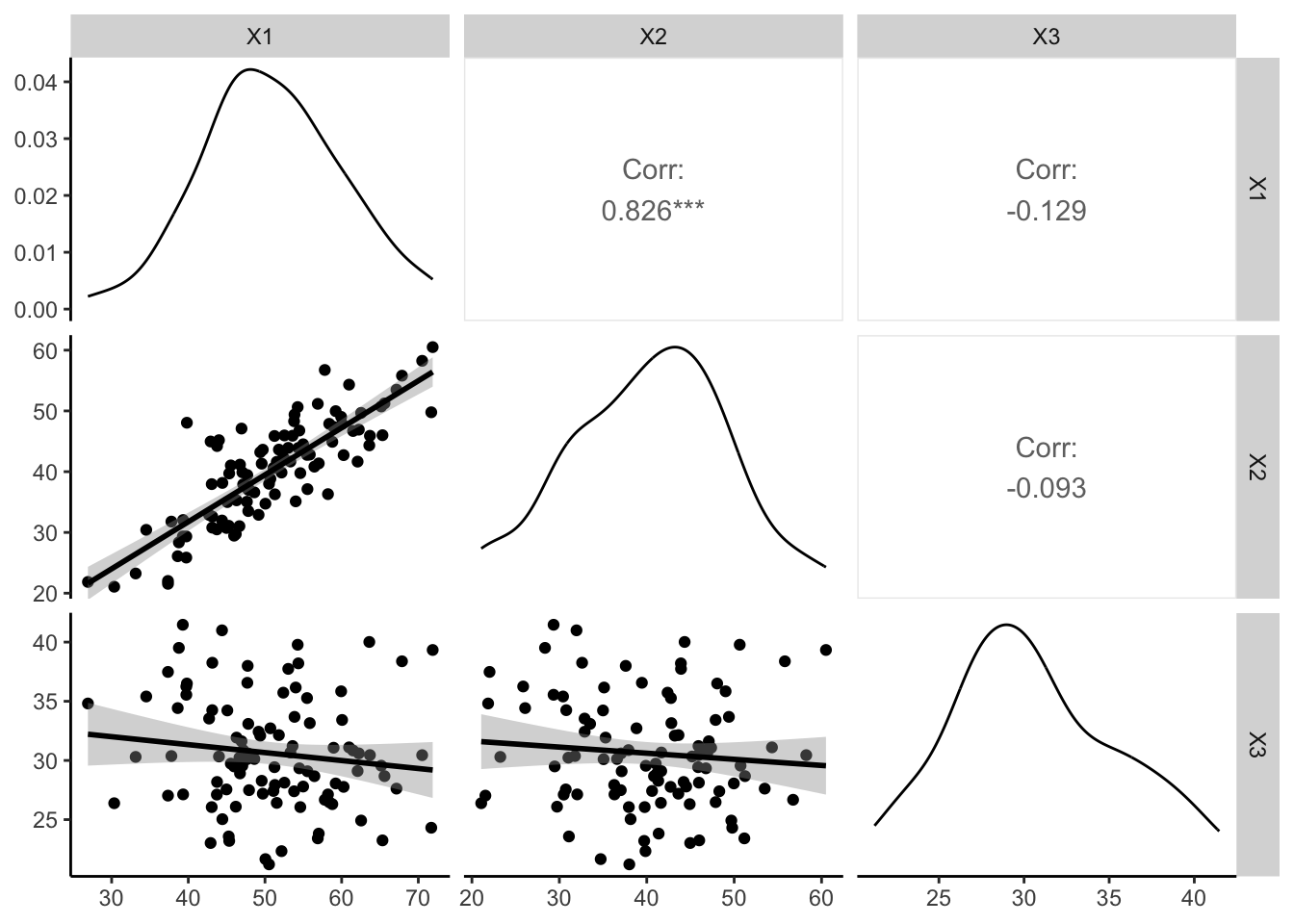
Figura 30.8: Multicolinearidade entre variáveis candidatas em modelos de regressão multivariável.

O pacote GGally²⁸⁴ fornece a função ggpairs para criar uma matriz gráfica de correlações bivariadas.

O pacote car²⁹¹ fornece a função vif para calcular o fator de inflação da variância (VIF).

30.5.3 O que fazer em caso de multicolinearidade elevada?

• Verifique a transformação (codificação) de variáveis numéricas em categóricas.²⁸³

• Aumente o tamanho da amostra, se possível, para reduzir a multicolinearidade.²⁸³

• Combine níveis de variáveis categóricas com baixa frequência de ocorrência.²⁸³

• Combine variáveis numéricas altamente correlacionadas em uma única variável composta, como a média ou soma das variáveis.²⁸³

• Considere a exclusão de variáveis altamente correlacionadas do modelo, especialmente se elas não forem essenciais para a análise.²⁸³

• Use técnicas de seleção de variáveis, como seleção passo a passo, para identificar e remover variáveis redundantes.²⁸³

• Use técnicas de regularização, como regressão ridge ou lasso, que podem lidar com multicolinearidade ao penalizar coeficientes de regressão.²⁸³

30.6 Redução de dimensionalidade

30.6.1 Correlação bivariada pode ser usada para seleção de variáveis em modelos de regressão multivariável?

• Seleção bivariada de variáveis - isto é, aplicação de testes de correlação em pares de variáveis candidatas e variável de desfecho afim de selecionar quais serão incluídas no modelo multivariável - é um dos erros mais comuns na literatura.^272,290,292

• A seleção bivariada de variáveis torna o modelo mais suscetível a otimismo no ajuste se as variáveis de confundimento não são adequadamente controladas.^290,292

30.6.2 Variáveis sem significância estatística devem ser excluídas do modelo final?

• Eliminar uma variável de um modelo significa anular o seu coeficiente de regressão (\(\beta = 0\)), mesmo que o valor estimado pelos dados seja outro. Desta forma, os resultados se afasTAM de uma solução de máxima verossimilhança (que tem fundamento teórico) e o modelo resultante é intencionalmente subótimo.²⁷²

• Os coeficientes de regressão geralmente dependem do conjunto de variáveis do modelo e, portanto, podem mudam de valor (“mudança na estimativa” positiva ou negativa) se uma (ou mais) variável(is) for(em) eliminada(s) do modelo.²⁷²

30.6.3 Por que métodos de regressão gradual não são recomendados para seleção de variáveis em modelos de regressão multivariável?

• Métodos diferentes de regressão gradual podem produzir diferentes seleções de variáveis de um mesmo banco de dados.²⁸⁸

• Nenhum método de regressão gradual garante a seleção ótima de variáveis de um banco de dados.²⁸⁸

• As regras de término da regressão baseadas em P-valor tendem a ser arbitrárias.²⁸⁸

30.6.4 O que pode ser feito para reduzir o número de variáveis candidatas em modelos de regressão multivariável?

• Em caso de uma proporção baixa entre o número de participantes e de variáveis, use o conhecimento prévio da literatura para selecionar um pequeno conjunto de variáveis candidatas.²⁹⁰

• Colapse categorias com contagem nula (células com valor igual a 0) de variáveis candidatas.²⁹⁰

• Use simulações de dados para identificar qual(is) variável(is) está(ão) causando problemas de convergência do ajuste do modelo.²⁹⁰

• A eliminação retroativa tem sido recomendada como a abordagem de regressão gradual mais confiável entre aquelas que podem ser facilmente alcançadas com programas de computador.²⁷²

30.6.5 Quando devemos forçar uma variável no modelo?

• Sempre que houver base teórica ou evidência prévia forte (por exemplo, idade em estudos de câncer), ou se for a variável de exposição principal.²⁹³

30.7 Suposições dos modelos de regressão

30.7.1 Quais suposições são feitas para regressão?

• As suposições dos modelos de regressão incluem linearidade, independência, homocedasticidade, normalidade dos resíduos e ausência de multicolinearidade.^REF?

30.7.2 Como avaliar as suposições de uma regressão?

• Usando diagnóstico de regressão (ex.: análise de resíduos, gráficos de valores observados vs. preditos) e comparação com análises estratificadas.²⁹³

Figura 30.9: Diagnóstico de regressão para avaliar suposições do modelo: linearidade, normalidade dos resíduos, homocedasticidade e alavancagem.

Citar como:
Ferreira, Arthur de Sá. Ciência com R: Perguntas e respostas para pesquisadores e analistas de dados. Rio de Janeiro: 1a edição,

Referências

192.

Sjoberg DD, Whiting K, Curry M, Lavery JA, Larmarange J. Reproducible Summary Tables with the gtsummary Package. The R Journal. 2021;13:570–580. doi:10.32614/RJ-2021-053

199.

Bandoli G, Palmsten K, Chambers CD, Jelliffe-Pawlowski LL, Baer RJ, Thompson CA. Revisiting the Table 2 fallacy: A motivating example examining preeclampsia and preterm birth. Paediatric and Perinatal Epidemiology. 2018;32(4):390–397. doi:10.1111/ppe.12474

251.

Greenhalgh T. How to read a paper: Statistics for the non-statistician. II: ̈Significanẗ relations and their pitfalls. BMJ. 1997;315(7105):422–425. doi:10.1136/bmj.315.7105.422

272.

Heinze G, Dunkler D. Five myths about variable selection. Transplant International. 2016;30(1):6–10. doi:10.1111/tri.12895

283.

Kim JH. Multicollinearity and misleading statistical results. Korean Journal of Anesthesiology. 2019;72(6):558–569. doi:10.4097/kja.19087

284.

Schloerke B, Cook D, Larmarange J, et al. GGally: Extension to ’ggplot2’.; 2024. doi:10.32614/CRAN.package.GGally

285.

Arel-Bundock V. modelsummary: Data and Model Summaries in R. Journal of Statistical Software. 2022;103. doi:10.18637/jss.v103.i01

286.

Hidalgo B, Goodman M. Multivariate or Multivariable Regression? American Journal of Public Health. 2013;103(1):39–40. doi:10.2105/ajph.2012.300897

287.

Suits DB. Use of Dummy Variables in Regression Equations. Journal of the American Statistical Association. 1957;52(280):548–551. doi:10.1080/01621459.1957.10501412

288.

Healy MJ. Statistics from the inside. 16. Multiple regression (2). Archives of Disease in Childhood. 1995;73(3):270–274. doi:10.1136/adc.73.3.270

289.

Kaplan J. fastDummies: Fast Creation of Dummy (Binary) Columns and Rows from Categorical Variables.; 2023. https://CRAN.R-project.org/package=fastDummies.

290.

Sun GW, Shook TL, Kay GL. Inappropriate use of bivariable analysis to screen risk factors for use in multivariable analysis. Journal of Clinical Epidemiology. 1996;49(8):907–916. doi:10.1016/0895-4356(96)00025-x

291.

Fox J, Weisberg S. An R Companion to Applied Regression. Sage Publications, Inc.; 2019. https://www.john-fox.ca/Companion/.

292.

DALES LG, URY HK. An Improper Use of Statistical Significance Testing in Studying Covariables. International Journal of Epidemiology. 1978;7(4):373–376. doi:10.1093/ije/7.4.373

293.

Greenland S. Modeling and variable selection in epidemiologic analysis. American Journal of Public Health. 1989;79(3):340–349. doi:10.2105/ajph.79.3.340