Capítulo 27 Correlação

27.1 Análise inferencial de correlação

27.1.1 O que é covariância?

.^REF?

27.1.2 O que é correlação?

.^REF?

27.1.3 Qual é a interpretação das medidas de correlação?

Os valores de correlação estão no intervalo \([-1; 1]\).^82,235,236
Valores de correlação positivos representam uma relação direta entre as variáveis, tal que valores maiores de uma variável estão associados a valores maiores de outra variável.^235,236
Valores de correlação negativos representam uma relação indireta (ou inversa) entre as variáveis, tal que valores maiores (menores) de uma variável estão associados a valores maiores (menores) de outra variável.^235,236
Valores de correlação próximos de \(0\) representam a inexistência de relação entre as variáveis.^235,236

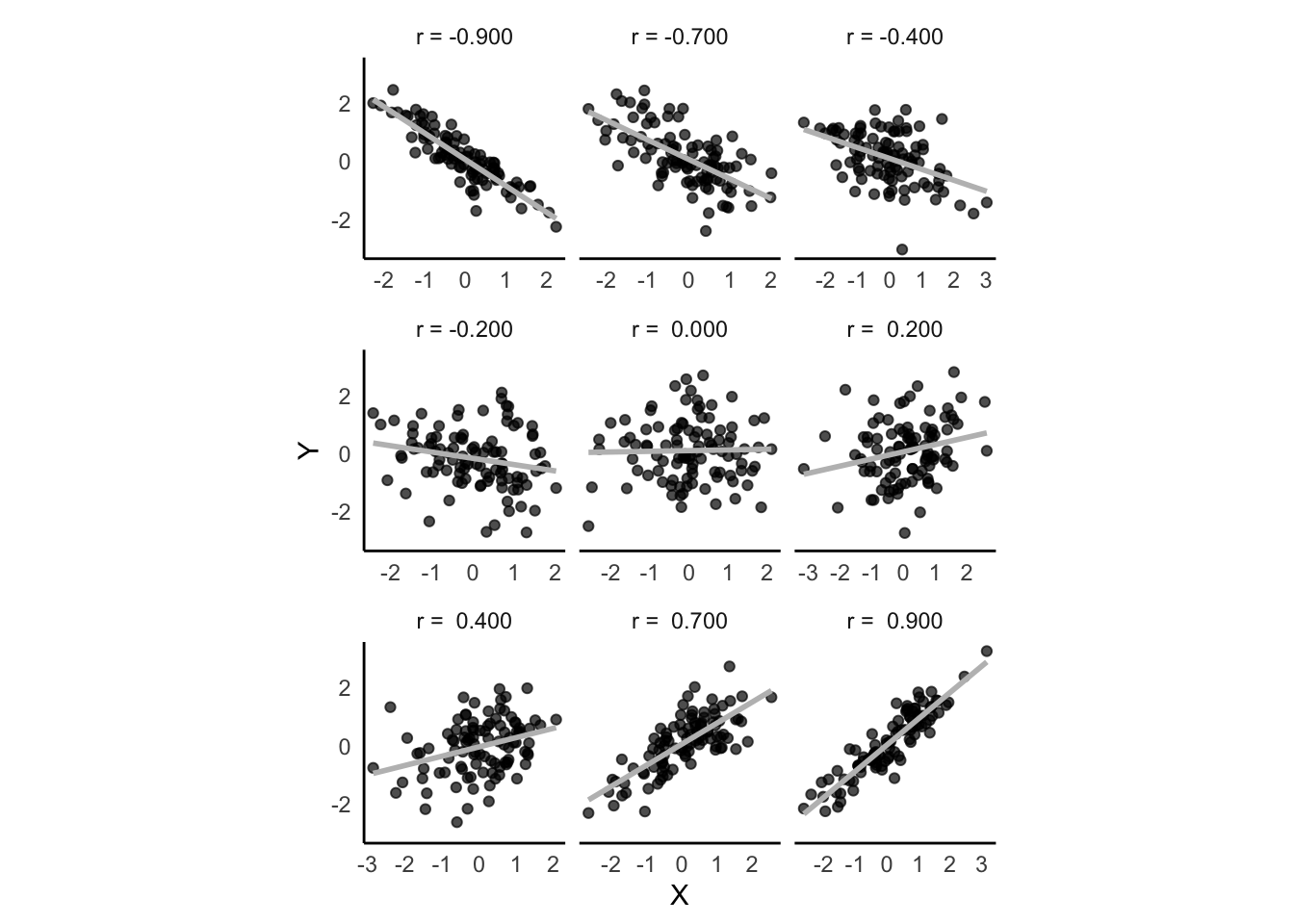
Figura 27.1: Exemplo de diferentes forças e direção de correlação entre duas variáveis X e Y.

27.1.4 Quais precauções devem ser tomadas na interpretação de medidas de correlação?

Tamanhos de efeito grande (ou qualquer outro) não representam necessariamente uma relação causa-efeito entre as variáveis.²³⁵
Tamanhos de efeito grande (ou qualquer outro) não representam necessariamente uma relação de concordância ou confiabilidade entre as variáveis.²³⁵
Uma escala de medição com representação agregada do constructo na coleta de dados pode subestimar o tamanho do efeito da correlação \(r\) em de cerca de 13% e do coeficiente de determinação \(R^2\) de cerca de 30%.⁴¹ Neste caso, a correlação desatenuada \(r_{x'y'}\) pode ser calculada pela equação (27.1), utilizando a correlação observada \(r_{xy}\) e os fatores de correção \(r_{xx'}\) e \(r_{yy'}\) para o número de intervalos nas variáveis X e Y, respectivamennte:⁴¹

\[\begin{equation} \tag{27.1} r_{x'y'} = \dfrac{r_{xy}}{r_{xx'}r_{yy'}} \end{equation}\]

O pacote psychmeta²³⁷ fornece a função correct_r_coarseness para calcular o coeficiente de correlação desatenuado (\(r_{x'y'}\)).

O pacote psychmeta²³⁷ fornece a função correct_r para calcular o coeficiente de correlação em escala restrita e/ou com erro de mensuração (\(r_{x'y'}\)).

Os coeficientes de correlação possuem suposições que, se violadas, podem levar a interpretações equivocadas. Nestes cenários, visualizar os dados e as relações entre as variáveis pode contribuir com a interpretação e utilidade dos coeficientes de correlação.²³⁸
O quarteto de Anscombe é um conjunto de quatro bancos de dados bivariados que possuem a mesma média, variância, correlação e regressão linear (até a 2a casa decimal), mas que são visualmente diferentes e, assim, demonstram a importância da análise gráfica da correlação.²³⁸

Tabela 27.1: Quarteto de Anscombe.
ID	x1	x2	x3	x4	y1	y2	y3	y4
1	10	10	10	8	8.04	9.14	7.46	6.58
2	8	8	8	8	6.95	8.14	6.77	5.76
3	13	13	13	8	7.58	8.74	12.74	7.71
4	9	9	9	8	8.81	8.77	7.11	8.84
5	11	11	11	8	8.33	9.26	7.81	8.47
6	14	14	14	8	9.96	8.10	8.84	7.04
7	6	6	6	8	7.24	6.13	6.08	5.25
8	4	4	4	19	4.26	3.10	5.39	12.50
9	12	12	12	8	10.84	9.13	8.15	5.56
10	7	7	7	8	4.82	7.26	6.42	7.91
11	5	5	5	8	5.68	4.74	5.73	6.89

Tabela 27.1: Análise descritiva do Quarteto de Anscombe demostrando os conjuntos de dados bivariados com parâmetros quase idênticos.
	X1Y1	X2Y2	X3Y3	X4Y4
Observações	11.00	11.00	11.00	11.00
Média x	9.00	9.00	9.00	9.00
Média y	7.50	7.50	7.50	7.50
Variância x	11.00	11.00	11.00	11.00
Variância y	4.13	4.13	4.12	4.12
Correlação	0.82	0.82	0.82	0.82
Coeficiente angular	0.50	0.50	0.50	0.50
Coeficiente linear	3.00	3.00	3.00	3.00
Coeficiente de determinação	0.67	0.67	0.67	0.67

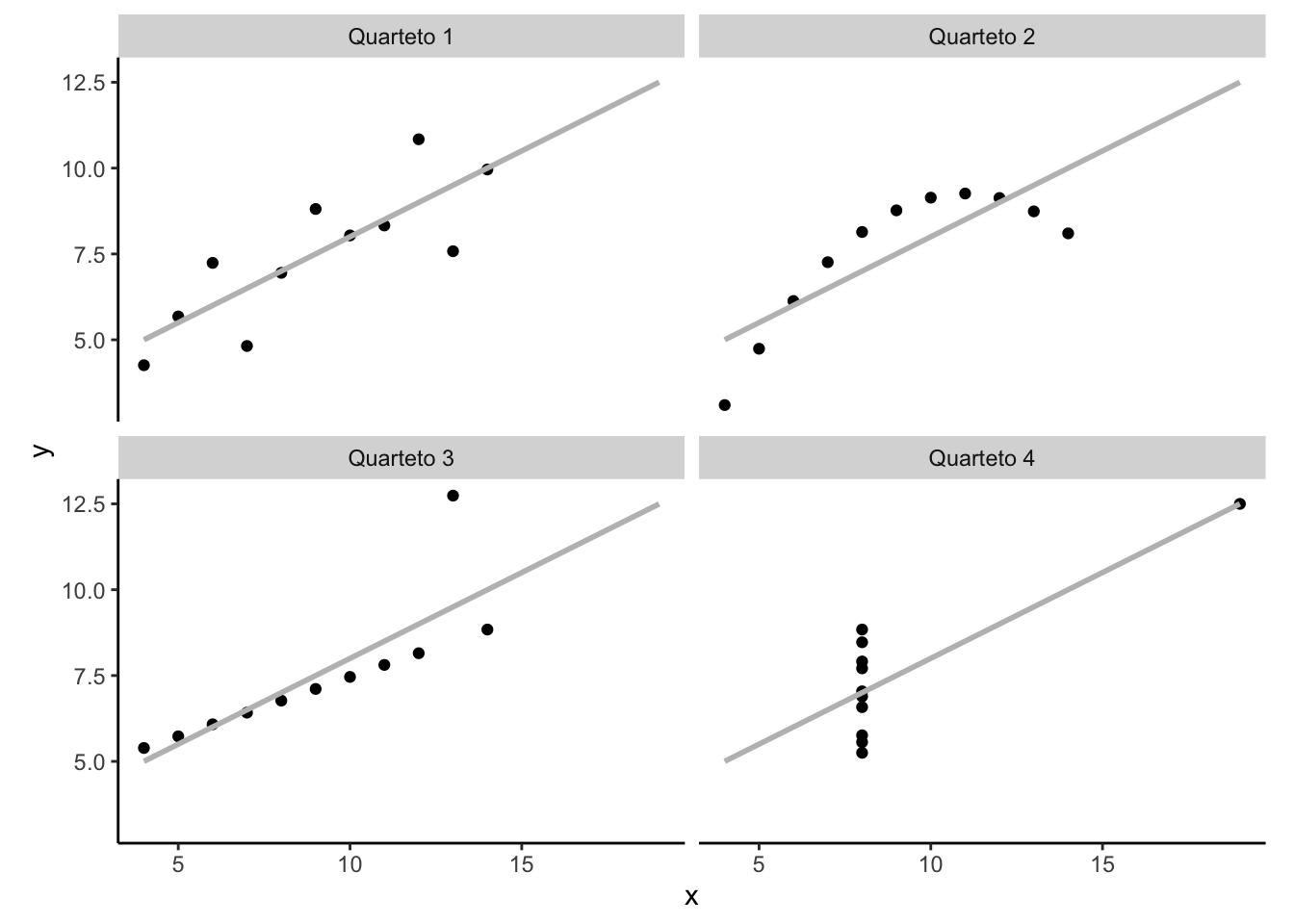
Gráfico de dispersão do Quarteto de Anscombe para representação gráfica de conjuntos de dados bivariados com parâmetros quase idênticos e relações muito distintas.

Figura 27.2: Gráfico de dispersão do Quarteto de Anscombe para representação gráfica de conjuntos de dados bivariados com parâmetros quase idênticos e relações muito distintas.

O pacote anscombiser²³⁹ fornece a função anscombise para gerar bancos de dados que compartilham os mesmos valores de parâmetros do Quarteto de Anscombe.

27.2 Coeficientes de correlação

27.2.1 Quais coeficientes podem ser usados em análises de correlação?

Coeficiente de correlação de Pearson (\(r\)).^235,236
- O coeficiente de correlação de Pearson (\(r\)) avalia a força e direção da relação linear entre duas variáveis quantitativas.^235,236
- Tipo: paramétrico.^235,236
- Hipóteses:²³⁶
  - Nula (\(H_{0}\)): \(r=0\)
  - Alternativa (\(H_{1}\)): \(r≠0\)
- Tamanho do efeito:^235,236
  - Coeficiente de correlação de Pearson (\(r\))

O pacote stats⁴⁴ fornece a função cor.test para calcular o coeficiente de correlação de Pearson (\(r\)).

O pacote correlation²⁴⁰ do projeto easystats²⁴¹ fornece a função correlation para calcular o coeficiente de correlação de Pearson (\(r\)).

Coeficiente de correlação ponto-bisserial (\(r_{s}\)).²³⁵
- O coeficiente de correlação ponto-bisserial (\(r_{s}\)) avalia a força e direção da relação linear entre uma variável quantitativa e outra dicotômica.²³⁵
- Tipo: paramétrico.²³⁵
- Hipóteses:²³⁵
  - Nula (\(H_{0}\)): \(r_{s}=0\)
  - Alternativa (\(H_{1}\)): \(r_{s}≠0\)
- Tamanho do efeito:²³⁵
  - Coeficiente de correlação ponto-bisserial (\(r_{s}\))

O pacote stats⁴⁴ fornece a função cor.test para calcular o coeficiente de correlação ponto-bisserial (\(r_{s}\)).

O pacote correlation²⁴⁰ do projeto easystats²⁴¹ fornece a função correlation para calcular o coeficiente de correlação ponto-bisserial (\(r_{s}\)).

Coeficiente de correlação de Spearman (\(\rho\)).^235,236
- O coeficiente de correlação de Spearman (\(\rho\)) avalia a força e direção da relação monotônica entre duas variáveis quantitativas.^235,236
- O coeficiente de correlação de Spearman (\(\rho\)) pode ser também definida como a correlação de Pearson (\(r\)) entre as classificações (ranks) das duas variáveis quantitativas.^235,236
- Tipo: não-paramétrico.^235,236
- Hipóteses:^235,236
  - Nula (\(H_{0}\)): \(\rho=0\)
  - Alternativa (\(H_{1}\)): \(\rho≠0\)
- Tamanho do efeito:^235,236
  - Coeficiente de correlação de Spearman (\(\rho\))

O pacote stats⁴⁴ fornece a função cor.test para calcular o coeficiente de correlação de Spearman (\(\rho\)).

O pacote correlation²⁴⁰ do projeto easystats²⁴¹ fornece a função correlation para calcular o coeficiente de correlação de Spearman (\(\rho\)).

Coeficiente de Kendall (\(\tau\)).^235,236
- O coeficiente Kendall \(\tau\) avalia a força e direção da relação monotônica entre duas variáveis quantitativas ou qualitativas.^235,236
- O coeficiente Kendall \(\tau\) é definido como a proporção de todos os pares concordantes menos a proporção de todos os pares discordantes.^235,236
- Tipo: não-paramétrico.^235,236
- Hipóteses:^235,236
  - Nula (\(H_{0}\)): \(\tau=0\)
  - Alternativa (\(H_{1}\)): \(\tau≠0\)
- Tamanho do efeito:^235,236
  - Kendall \(\tau\)

O pacote stats⁴⁴ fornece a função cor.test para calcular o coeficiente Kendall \(\tau\).

O pacote correlation²⁴⁰ do projeto easystats²⁴¹ fornece a função correlation para calcular o coeficiente coeficiente Kendall \(\tau\).

Coeficiente de Cramér (\(V\)).^REF?
- O coeficiente Cramér (\(V\)) avalia a força e direção da relação entre duas variáveis qualitativas.^REF?
- Tipo: não-paramétrico.^REF?
- Hipóteses:^REF?
  - Nula (\(H_{0}\)): \(V=0\)
  - Alternativa (\(H_{1}\)): \(V≠0\)
- Tamanho do efeito:^REF?
  - Coeficiente Cramer (\(V\))

Coeficiente de Sheperd \(\phi\).^REF?
- O coeficiente Phi (\(\phi\)) avalia a força e direção da relação entre duas variáveis dicotômicas.^REF?
- Tipo: não-paramétrico.^REF?
- Hipóteses:^REF?
  - Nula (\(H_{0}\)): \(\phi=0\)
  - Alternativa (\(H_{1}\)): \(\phi≠0\)
- Tamanho do efeito:^REF?
  - Coeficiente Phi (\(\phi\))

O pacote correlation²⁴⁰ do projeto easystats²⁴¹ fornece a função correlation para calcular o coeficiente coeficiente Sheperd \(\phi\).

O pacote corrplot¹⁵⁴ fornece a função cor.mtest para calcular os P-valores e intervalos de confiança da matriz de correlação.

O pacote corrplot¹⁵⁴ fornece a função corrplot para visualização da matriz de correlação.

Referências

41.

Aguinis H, Pierce CA, Culpepper SA. Scale Coarseness as a Methodological Artifact. Organizational Research Methods. 2008;12(4):623-652. doi:10.1177/1094428108318065

44.

R Core Team. R: A Language and Environment for Statistical Computing.; 2023. https://www.R-project.org/.

82.

Barkan H. Statistics in clinical research: Important considerations. Annals of Cardiac Anaesthesia. 2015;18(1):74. doi:10.4103/0971-9784.148325

154.

Wei T, Simko V. R package corrplot: Visualization of a correlation matrix. 2021. https://github.com/taiyun/corrplot.

235.

Khamis H. Measures of Association: How to Choose? Journal of Diagnostic Medical Sonography. 2008;24(3):155-162. doi:10.1177/8756479308317006

236.

Allison JS, Santana L, (Jaco) Visagie IJH. A primer on simple measures of association taught at undergraduate level. Teaching Statistics. 2022;44(3):96-103. doi:10.1111/test.12307

237.

Dahlke JA, Wiernik BM. Psychmeta: An r package for psychometric meta-analysis. 2019;43. doi:10.1177/0146621618795933

238.

Anscombe FJ. Graphs in Statistical Analysis. The American Statistician. 1973;27(1):17-21. doi:10.1080/00031305.1973.10478966

239.

Northrop PJ. Anscombiser: Create Datasets with Identical Summary Statistics.; 2022. https://CRAN.R-project.org/package=anscombiser.

240.

Makowski D, Wiernik BM, Patil I, Lüdecke D, Ben-Shachar MS. Correlation: Methods for Correlation Analysis.; 2022. https://CRAN.R-project.org/package=correlation.

241.

Lüdecke D, Ben-Shachar MS, Patil I, et al. Easystats: Framework for Easy Statistical Modeling, Visualization, and Reporting.; 2022. https://easystats.github.io/easystats/.