Capítulo 1 Pensamento probabilístico
1.2 Espaço amostral e eventos discretos
1.2.1 O que é espaço amostral discreto?
O espaço amostral \(S\) de um experimento aleatório é definido como o conjunto de todos os desfechos possíveis de um experimento.1
Em probabilidade discreta, o espaço amostral \(S\) pode ser enumerado e contato.1
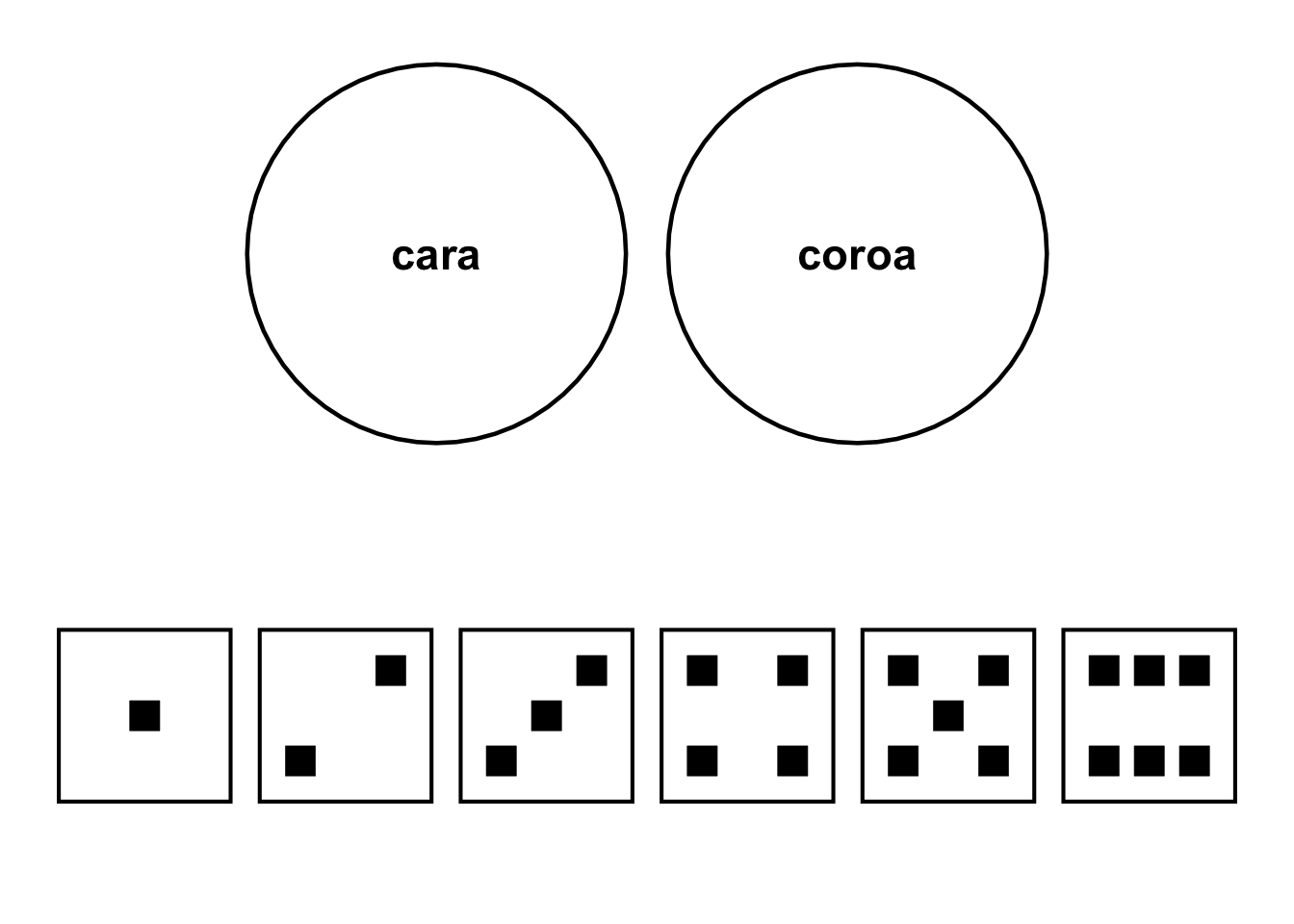
Figura 1.1: Exemplos de espaço amostral discreto. Superior: Todas as faces de uma moeda. Inferior: Todas as faces de um dado.
1.2.2 O que é evento discreto?
Um evento \(E\) é um único desfecho ou uma coleção de desfechos.1
Um evento \(E\) é um subconjunto do espaço amostral \(S\) de um experimento.1
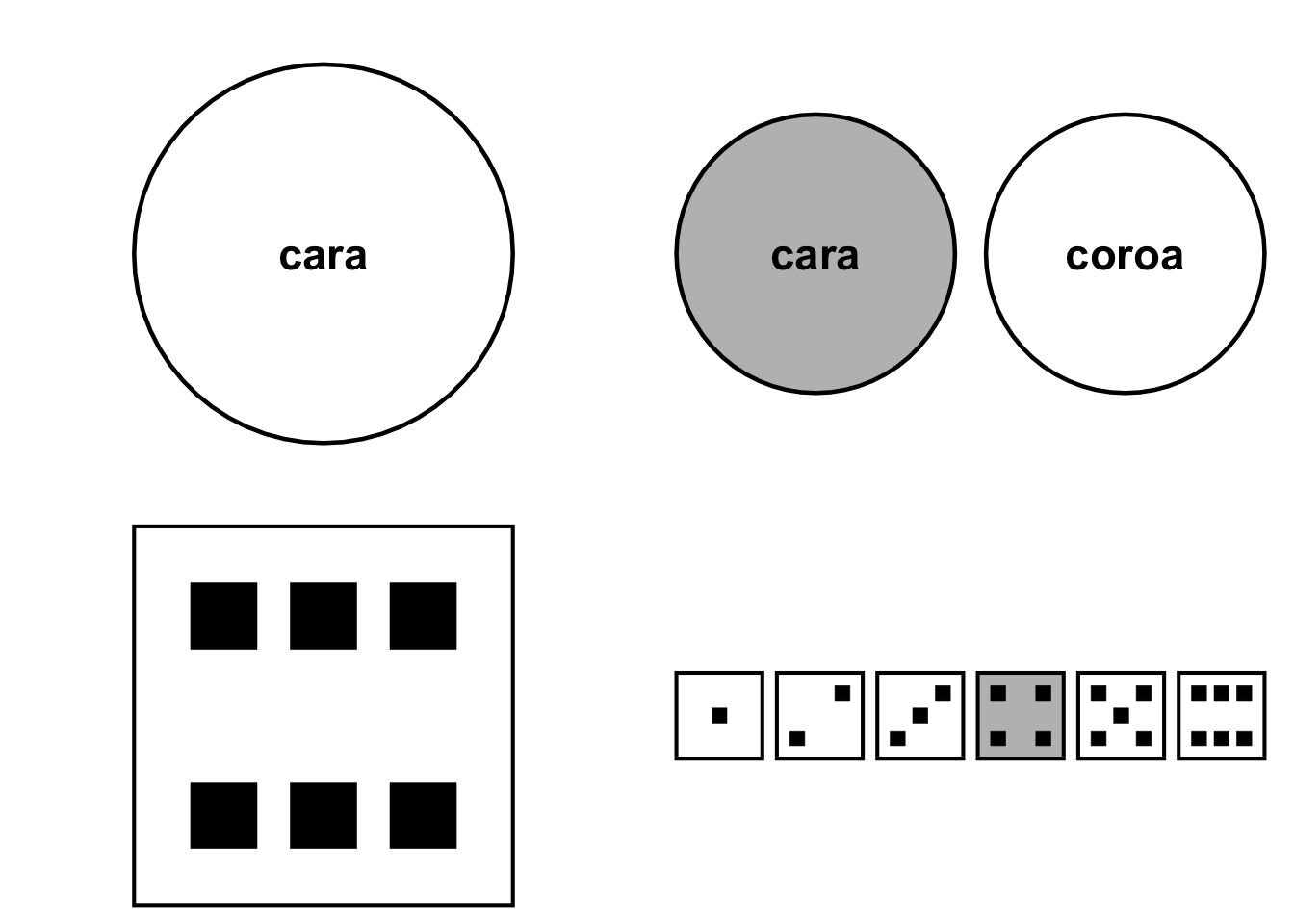
Figura 1.2: Exemplos de evento de experimento. Superior: 1 lançamento de 1 moeda. Inferior: 1 lançamento de 1 dado.
1.2.3 O que é espaço de eventos discretos?
Um espaço de eventos \(E_{s}\) também é um subconjunto do espaço amostral \(S\) de um experimento.1
A união de dois eventos \(E_{1} \cup E_{2}\) é o conjunto de todos os desfechos que estão em ambos.1
A intersecção de dois eventos \(E_{1} \cap E_{2}\), ou evento conjunto, é o conjunto de todos os desfechos que estão em ambos os eventos.1
O complemento de um evento \(E^C\) consiste em todos os desfechos que não estão incluídos no evento \(E\).1
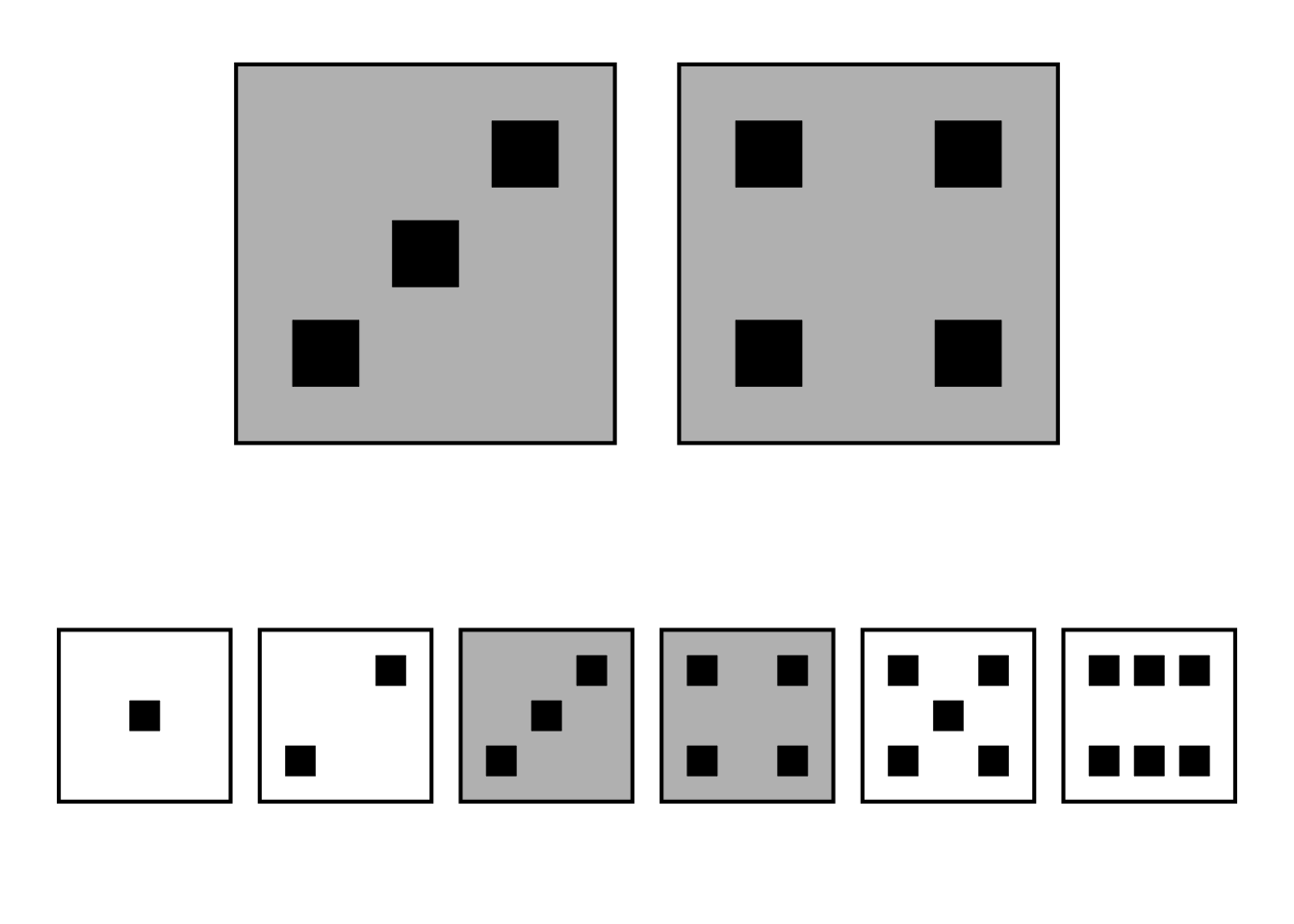
Figura 1.3: Espaço de eventos: União dos eventos face = 3 e face = 4 de um dado.
1.4 Probabilidade
1.4.1 O que é probabilidade?
Com um espaço amostral \(S\) finito e não vazio de desfechos igualmente prováveis, a probabilidade \(P\) de um evento \(E\) é a razão entre o número de desfechos no evento \(E\) e o número de desfechos no espaço amostral \(S\).1
Um evento \(E\) impossível não contém um desfecho e, portanto, nunca ocorre: \(P(E)=0\).1,2
Um evento \(E\) é certo consiste em qualquer um dos desfechos possíveis e, portanto, sempre ocorre: \(P(E)=1\).1
1.4.2 Quais são os axiomas da probabilidade?
A probabilidade de um evento é um número real que satisfaz os seguintes axiomas descritos por Andrei Nikolaevich Kolmogorov em 1950:1,2
Axioma I. Probabilidades de um evento \(E\) são números não-negativos: \(P(E) \geq 0\).
Axioma II. Probabilidade de todos os eventos do espaço amostral \(A\) ocorrerem é 100%: \(P(S)=1\).
Axioma III. A probabilidade de um conjunto k de eventos mutuamente exclusivos é igual a soma da probabilidade de cada evento: \(P(E_{1} \cup E_{2} \cup ... E_{k}) = P(E_{1}) + P(E_{2}) + ... + P(E_{k})\).
Os axiomas possuem as seguintes consequências:1
A soma da probabilidade de dois eventos que dividem o espaço amostral é 100%: \(P(E)+P(E)^C=1\).
O valor máximo de probabilidade de um evento é 100%: \(P(S)≤1\).
A probabilidade é uma função não decrescente do número de desfechos de um evento.
1.5 Independência e probabilidade
1.5.1 O que é independência em estatística?
Em experimentos aleatórios, é comum assumir que os eventos de tentativas separadas são independentes devido a independência física de eventos e experimentos.1
Se a ocorrência do evento \(E_{1}\) não tiver efeito na ocorrência do evento \(E_{2}\), os eventos \(E_{1}\) e \(E_{2}\) são considerados estatisticamente independentes.
Eventos são mutuamente exclusivos, ou disjuntos, se a ocorrência de um exclui a ocorrência dos outros.1
Se dois eventos \(E_{1}\) e \(E_{2}\) são mutuamente exclusivos, então os eventos \(E_{1}\) e \(E_{2}\) não podem ocorrer ao mesmo tempo e, portanto, são eventos dependentes.
Em experimentos independentes, o desfecho de uma tentativa é independente dos desfechos de outras tentativas, passadas e/ou futuras. Uma tentativa em um experimento aleatório é independente se a probabilidade de cada desfecho possível não mudar de tentativa para tentativa.1
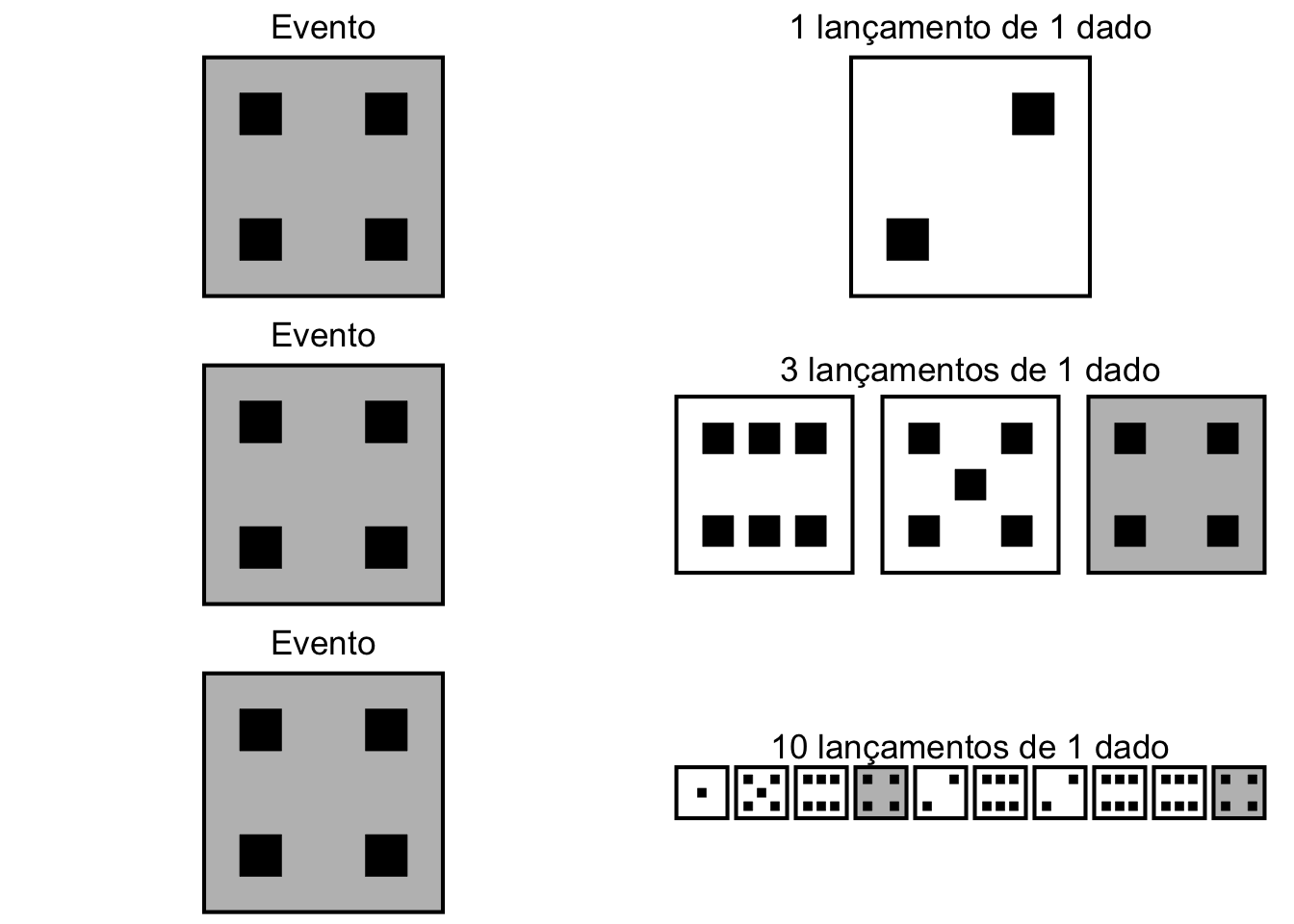
Figura 1.4: Esquerda: Evento (face = 4). Direita: Experimentos de 1 lançamento de 1 dado (superior), 3 lançamentos de 1 dado (central), 10 lançamentos de 1 dado (inferior).
1.5.2 O que é probabilidade marginal?
- Probabilidade marginal é a probabilidade de ocorrência de um evento \(E\) independentemente da(s) probabilidade(s) de outro(s) evento(s).1
1.5.3 O que é probabilidade conjunta?
Probabilidade conjunta é a probabilidade de ocorrência de dois ou mais eventos independentes \(E_{1}\), \(E_{2}\), …, \(E_{k}\), independentemente da(s) probabilidade(s) de outro(s) evento(s).1
Se a probabilidade conjunta dos eventos é nula (\(E_{1} \cup E_{2} = 0\)), esses dois eventos \(E_{1}\) e \(E_{2}\) são mutuamente exclusivos ou disjuntos.1
1.5.4 O que é probabilidade condicional?
Probabilidade condicional é a probabilidade de ocorrência do evento \(E_{2}\) quando se sabe que o evento \(E_{1}\) já ocorreu \(P(E_{2} | E_{1})\).1
A probabilidade condicional \(P(E_{2} | E_{1})\) representa que a ocorrência do evento \(E_{1}\) fornece informação sobre a ocorrência do evento \(E_{2}\).1
Se a ocorrência do evento \(E_{1}\) tiver alguma influência na ocorrência do evento \(E_{2}\), então a probabilidade condicional do evento \(E_{2}\) dado o evento \(E_{1}\) pode ser maior ou menor do que a probabilidade marginal.1
1.6 Leis dos números anômalos
1.6.1 O que é a lei dos números anômalos?
- A lei dos números anômalos - lei de Benford - é uma distribuição de probabilidade que descreve a frequência de ocorrência do primeiro dígito em muitos conjuntos de dados do mundo real.3
1.7 Leis dos pequenos números
1.7.1 O que é a lei dos pequenos números?
A crença exagerada na probabilidade de replicar com sucesso os achados de um estudo, pela tendência de se considerar uma amostra como representativa da população.4
A crença na lei dos pequenos números se refere à tendência de superestimar a estabilidade das estimativas provenientes de estudos com amostras pequenas.5
Quando se percebe um padrão, pode não ser possível identificar se tal padrão é real.6
1.8 Leis dos grandes números
1.8.1 O que é a lei dos grandes números?
A lei dos grandes números descreve que, ao realizar o mesmo experimento \(E\) um grande número de vezes (\(n\)), a média \(\mu\) dos resultados obtidos tende a se aproximar do valor esperado \(E[\bar{X}]\) à medida que mais experimentos forem realizados (\(n \to \infty\)).REF?
De acordo com a lei dos grandes números, a média amostral converge para a média populacional à medida que o tamanho da amostra aumenta.REF?
1.9 Teorema central do limite
1.9.1 O que é teorema central do limite?
- O teorema central do limite - equação (1.1) - afirma que, para uma amostra aleatória de tamanho \(n\) de uma população com valor esperado igual à média \(E[\bar{X_{i}}] = \mu\) e variância \(Var[\bar{X_{i}}]\) igual a \(\sigma^{2}\), a distribuição amostral da média de uma variável \(\bar{X}\) se aproxima de uma distribuição normal \(N\) com média \(\mu\) e variância \(\sigma^{2}/n\) à medida que \(n\) aumenta (\(n \to \infty\)):8
\[\begin{equation} \tag{1.1} \sqrt{n}(\bar{X} - \mu) \xrightarrow{n \to \infty} N(0, \sigma^2) \end{equation}\]
O teorema central do limite demonstra que se o tamanho da amostra \(n\) for suficientemente grande, a distribuição amostral das médias obtidas utilizando reamostragem com substituição será aproximadamente normal, com média \(\mu\) e variância \(\sigma^{2}/n\), independentemente da distribuição da população.8
No exemplo abaixo, uma variável aleatória numérica com distribuição uniforme no espaço amostral \(S=[18;65]\) tem média \(\mu\) = 38.53 e variância \(\sigma^{2}\) = 172.433. A distribuição amostral da média de 100 amostras de tamanho 5, 50, 500 e 5000 tomadas da população com reposição e igual probabilidade se aproxima de uma distribuição normal com média \(\mu\) = 38.493 e variância \(\sigma^{2}\) = 0.038, independentemente da distribuição da população:
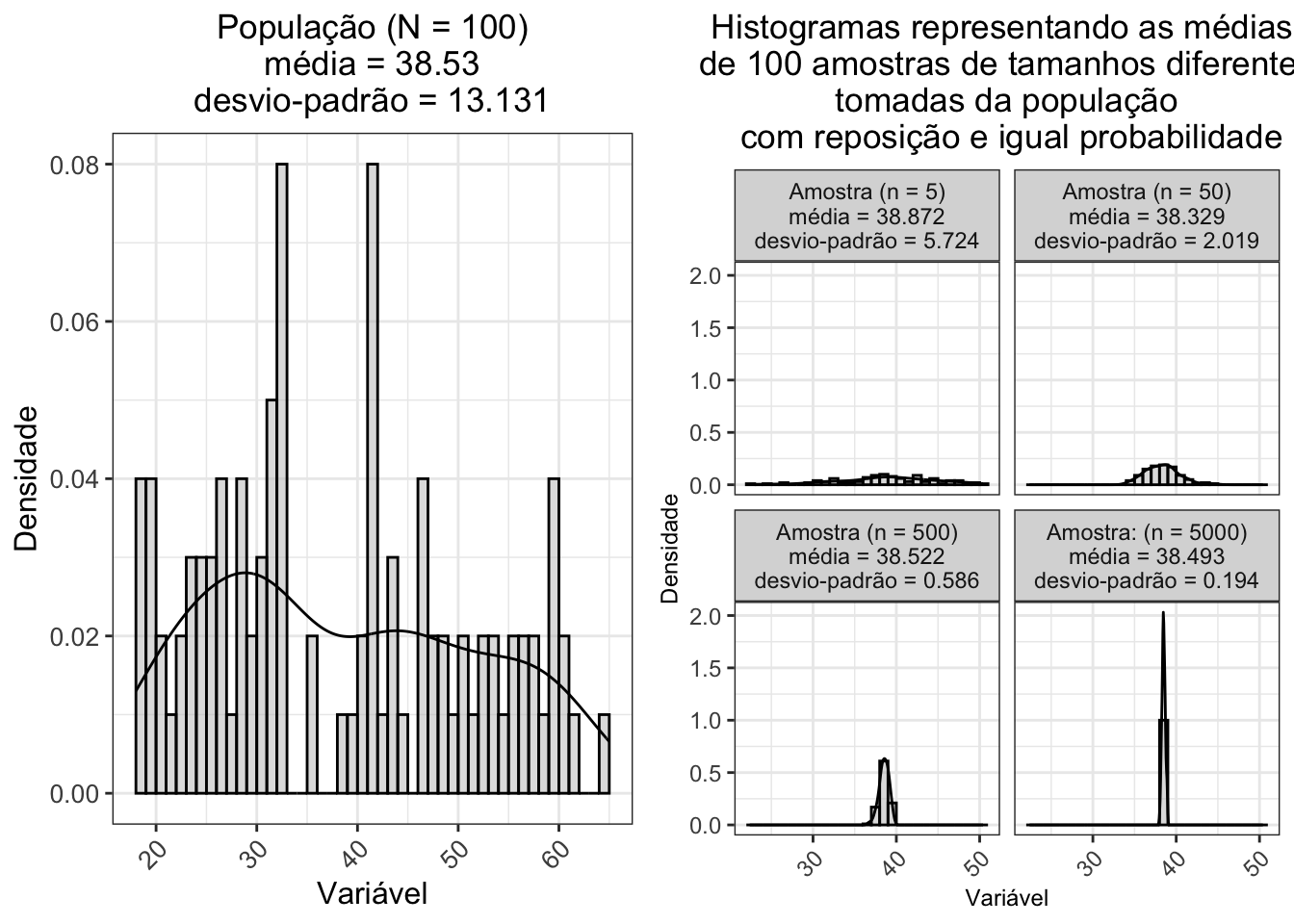
Figura 1.5: Esquerda: Histogramas de uma variável aleatória com distribuição uniforme (N = 100). Direita: Histogramas da média de 100 amostras de tamanhos 5, 50, 500 e 5000 tomadas da população com reposição e igual probabilidade.
- Em outro exemplo, o lançamento de um dado com distribuição uniforme no espaço amostral \(S=\{1,2,3,4,5,6\}\) tem média \(\mu\) = 3.77 e variância \(\sigma^{2}\) = 3.169. A distribuição amostral da média de 100 amostras de tamanho 5, 50, 500 e 5000 tomadas da população com reposição e igual probabilidade se aproxima de uma distribuição normal com média \(\mu\) = 3.767 e variância \(\sigma^{2}\) = 0.001, independentemente da distribuição da população:
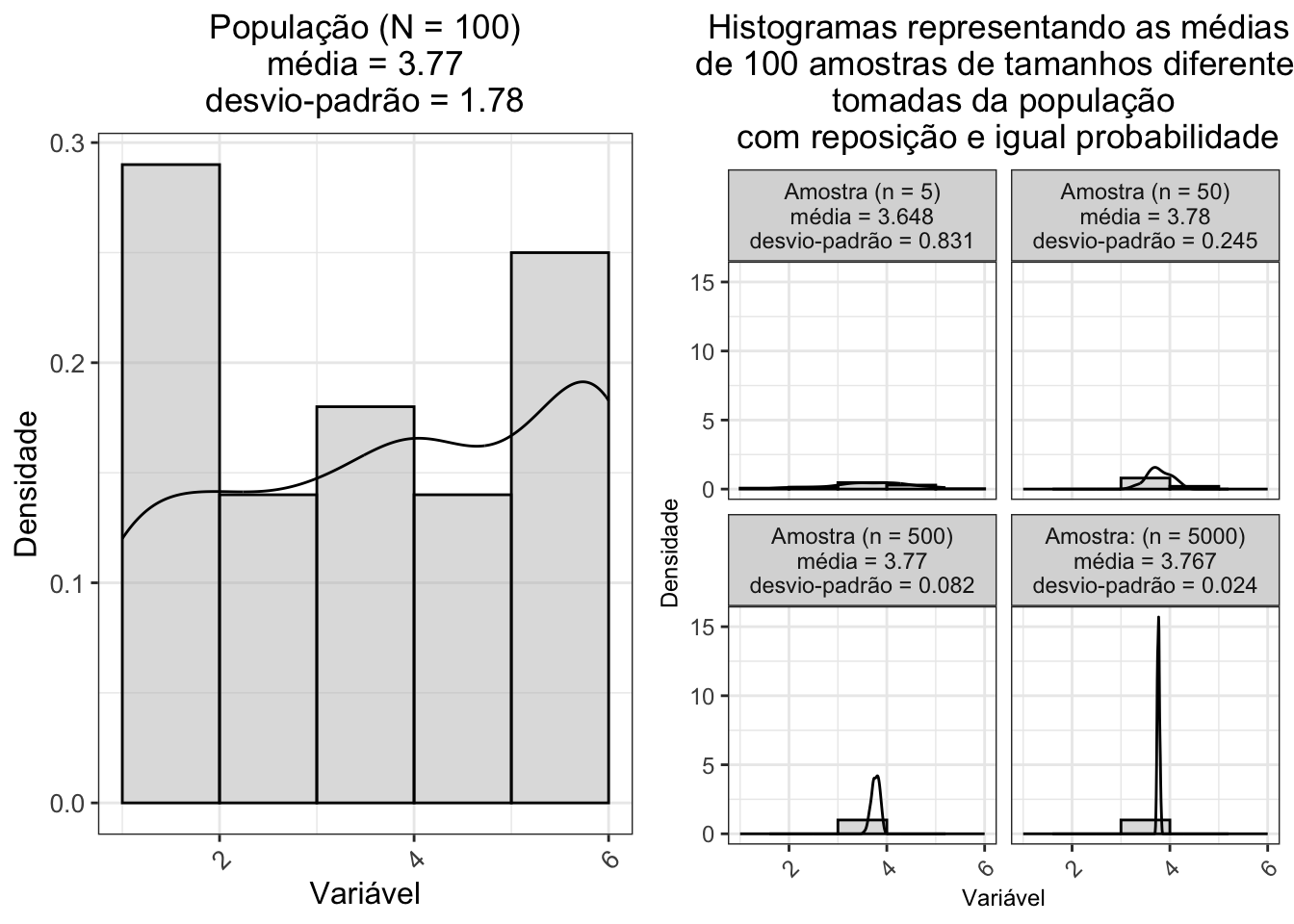
Figura 1.6: Esquerda: Histogramas de lançament de 1 dado com distribuição uniforme (N = 100). Direita: Histogramas da média de 100 amostras de tamanhos 5, 50, 500 e 5000 tomadas da população com reposição e igual probabilidade.
- Mais um exemplo, o lançamento de uma moeda com distribuição uniforme no espaço amostral \(S=\{0,1\}\) — codificado para \(sucesso = 1\) e \(insucesso = 0\) — tem média \(\mu\) = 0.5 e variância \(\sigma^{2}\) = 0.253. A distribuição amostral da média de 100 amostras de tamanho 5, 50, 500 e 5000 tomadas da população com reposição e igual probabilidade se aproxima de uma distribuição normal com média \(\mu\) = 0.501 e variância \(\sigma^{2}\) = 0, independentemente da distribuição da população:
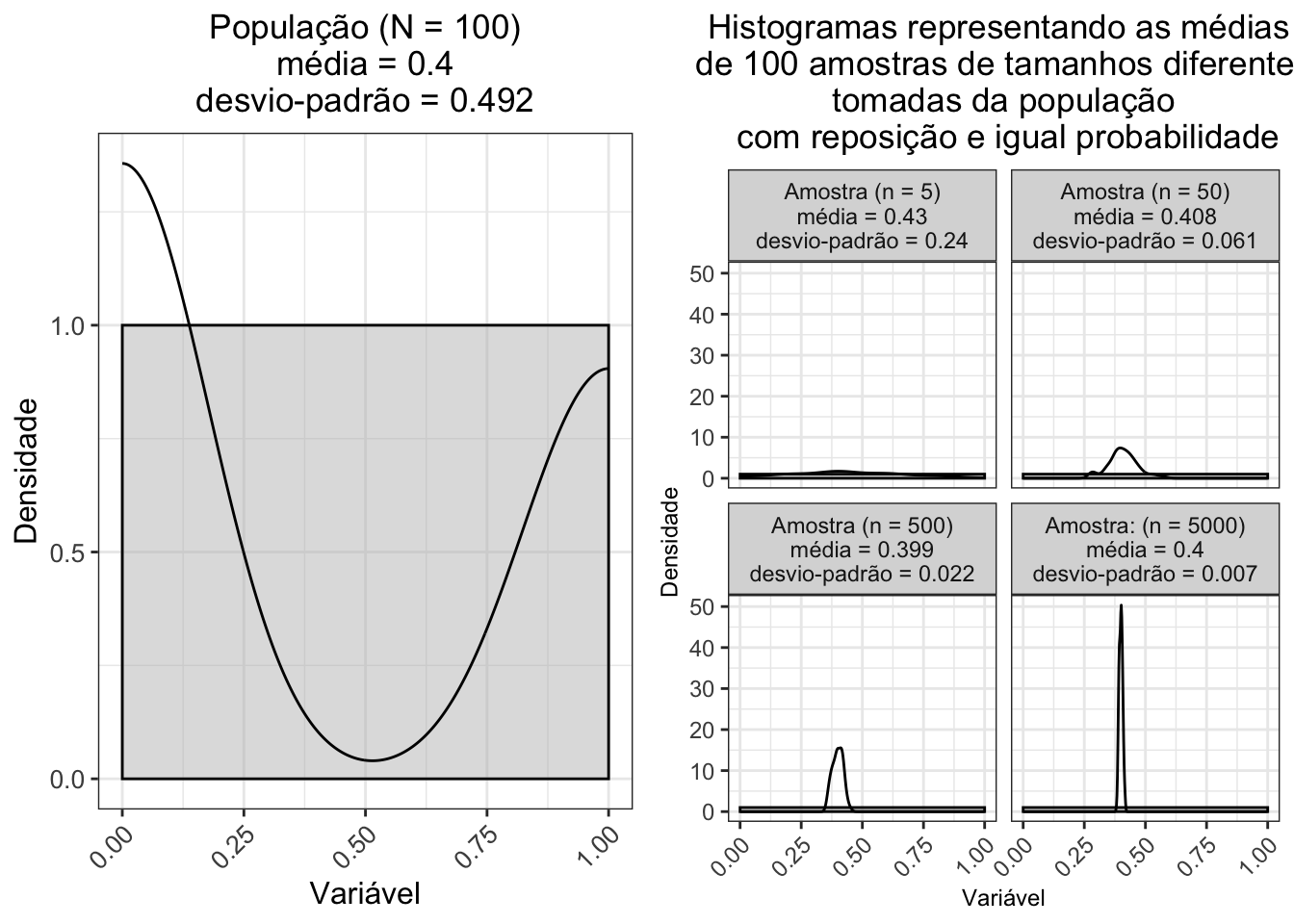
Figura 1.7: Esquerda: Histogramas de lançament de 1 moeda com distribuição uniforme (N = 100). Direita: Histogramas da média de 100 amostras de tamanhos 5, 50, 500 e 5000 tomadas da população com reposição e igual probabilidade.
1.9.2 Quais as condições de validade do teorema central do limite?
As condições de validade do teorema central do limite são:8
As variáveis aleatórias devem ser independentes e identicamente distribuídas (independent and identically distributed ou i.i.d.);
As variáveis aleatórias devem ter média \(\mu\) e variância \(\sigma^{2}\) finitas;
O tamanho da amostra deve ser suficientemente grande (geralmente, \(n \geq 30\)).
1.9.3 Qual a relação entre a lei dos grandes números e o teorema central do limite?
- A lei dos grandes números é um precursor do teorema central do limite, pois estabelece que a média da amostra se torna cada vez mais próxima da média populacional (isto é, mais representativa) à medida que o tamanho da amostra aumenta, e o teorema central do limite demonstra que o a distribuição da soma das variáveis aleatórias se aproxima de uma distribuição normal também à medida que o tamanho da amostra aumenta.REF?
1.9.4 Qual a relevância do teorema central do limite para a análise estatística?
O teorema central do limite explica porque os testes paramétricos têm maior poder estatístico do que os testes não paramétricos, os quais não requerem suposições de distribuição de probabilidade.8
O teorema central do limite implica que os métodos estatísticos que se aplicam a distibuições normais podem ser aplicados a outras distribuições quando suas suposições são satisfeitas.8
Como o teorema central do limite determina a distribuição amostral \(Z\) - equação (1.2) - das médias com tamanho amostral suficientemente grande, a média pode ser padronizada para uma distribuição normal com média 0 e variância 1, \(N(0,1)\):8
\[\begin{equation} \tag{1.2} Z = \frac{\bar{X} - \mu}{\sigma / \sqrt{n}} \end{equation}\]
- Para amostras com \(n \geq 30\), a distribuição amostral Student-t se aproxima da distribuição normal padrão \(Z\) e, portanto, as suposições sobre a distribuição populacional não são mais necessárias de acordo com o teorema central do limite. Neste cenário, a suposição de distribuição normal pode ser usada para a distribuição de probabilidade.8
1.10 Regressão para a média
1.10.1 O que é regressão para a média?
Regressão para a média9 é um fenômeno estatístico que ocorre quando uma variável aleatória \(X\) é medida na mesma unidade de análise em dois ou mais momentos diferentes, \(X_{1}\), \(X_{2}\), …, \(X_{t}\) e \(X_{t}\) é mais próximo da média populacional do que \(X_{1}\), ou seja, \(E(X_{t})\) é mais próxima de \(E(X)\) do que \(E(X_{1})\) é de \(E(X)\).10
O valor real - sem erros aleatório ou sistemático - em geral não é conhecido, mas pode ser estimado pela média de várias observações.10
Regressão para a média pode ocorrer em qualquer pesquisa cujo delineamento envolva medidas repetidas.11
Em medidas repetidas, a média de várias observações é mais próxima da média verdadeira do que qualquer observação individual, pois o erro aleatório é reduzido pela média.10
Valores extremos - em direção ao mínimo ou máximo - em uma medição inicial tendem a ser seguidos por valores mais próximos da média (valor real) na medição subsequente.10
No exemplo abaixo, a 2a medida (dado 2 = 121) é mais próxima da média (valor real = 120) do que a 1a medida (dado 1 = 118):
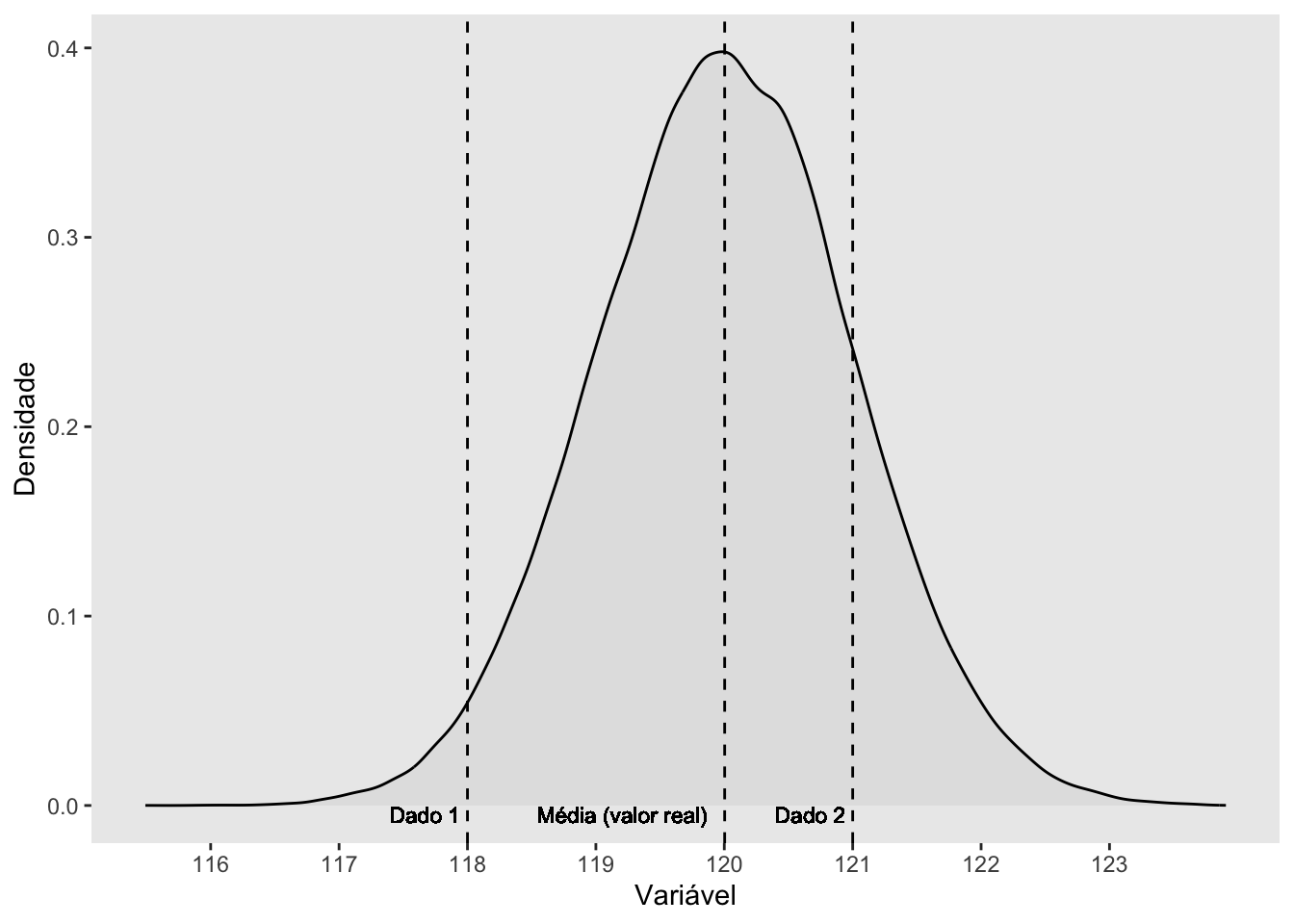
Figura 1.8: Representação gráfica da regressão para a média em medidas repetidas. A segunda medida (dado 2) é mais próxima da média (valor real) do que a primeira medida (dado 1).
1.10.2 Qual a causa da regressão para a média?
A regressão para a média pode ser atribuída ao erro aleatório, que é a variação não sistemática nos valores observados em torno de uma média verdadeira (por exemplo, erro de medição aleatório ou variações aleatórias em um participante).10
Regrssão para a média é uma consequência da observação de que dados extremos não se repetem com frequência.11
Deve-se assumir que a regressão para a média ocorreu até que os dados mostrem o contrário.10
1.10.3 Por que detectar o fenômeno de regressão para a média?
- A regressão para a média pode levar a conclusões errôneas sobre a eficácia de uma intervenção, pois a mudança observada pode ser devida ao erro aleatório e não ao tratamento.11
1.10.4 Com detectar o fenômeno de regressão para a média?
- O fenômeno de regressão para a média pode ser detectado por meio de gráfico de dispersão da diferença (estudos transversais) ou mudança (estudos longitudinais) versus os valores da 1a medida.10
O pacote regtomean12 fornece as funções cordata para calcular a correlação entre medidas tipo antes–e-depois e meechua_reg para ajustar modelos lineares de regressão.