Capítulo 12 Distribuições e parâmetros

12.1 Distribuições de probabilidade

12.1.1 O que são distribuições de probabilidade?

• Uma distribuição de probabilidade é uma função que descreve os valores possíveis ou o intervalo de valores de uma variável (eixo horizontal) e a frequência com que cada valor é observado (eixo vertical).⁴⁹

12.1.2 Como representar distribuições de probabilidade?

• Tabelas de frequência, polígonos de frequência, gráficos de barras, histogramas e boxplots são formas de representar distribuições de probabilidade.¹⁰⁰

• Tabelas de frequência mostram as categorias de medição e o número de observações em cada uma. É necessário conhecer o intervalo de valores (mínimo e máximo), que é dividido em intervalos arbitrários chamados “intervalos de classe”.¹⁰⁰

• Se houver muitos intervalos, não haverá redução significativa na quantidade de dados, e pequenas variações serão perceptíveis. Se houver poucos intervalos, a forma da distribuição não poderá ser adequadamente determinada.¹⁰⁰

• A quantidade de intervalos pode ser determinada pelo método de Sturges, que é dado pela fórmula \(k = 1 + 3.322 \times \log_{10}(n)\), onde \(k\) é o número de intervalos e \(n\) é o número de observações.¹⁰¹

• A quantidade de intervalos pode ser determinada pelo método de Scott, que é dado pela fórmula \(h = 3.5 \times \text{sd}(x) \times n^{-1/3}\), onde \(h\) é a largura do intervalo, \(\text{sd}(x)\) é o desvio padrão e \(n\) é o número de observações.¹⁰²

• A quantidade de intervalos pode ser determinada pelo método de Freedman-Diaconis, que é dado pela fórmula \(h = 2 \times \text{IQR}(x) \times n^{-1/3}\), onde \(h\) é a largura do intervalo, \(\text{IQR}(x)\) é o intervalo interquartil e \(n\) é o número de observações.¹⁰³

• A largura das classes pode ser determinada dividindo o intervalo total de observações pelo número de classes. Recomenda-se larguras iguais, mas larguras desiguais podem ser usadas quando existirem grandes lacunas nos dados ou em contextos específicos. Os intervalos devem ser mutuamente exclusivos e não sobrepostos, evitando intervalos abertos (ex.: <5, >10).¹⁰⁰

• Polígonos de frequência são gráficos de linhas que conectam os pontos médios de cada barra do histograma. Eles são úteis para comparar duas ou mais distribuições de frequência.¹⁰⁰

• Gráficos de barra verticais ou horizontais representam a distribuição de frequências de uma variável categórica. A altura de cada barra é proporcional à frequência da classe. A largura da barra é igual à largura da classe. A área de cada barra é proporcional à frequência da classe. A área total do gráfico de barras é igual ao número total de observações.¹⁰⁰

• Histogramas representam a distribuição de frequências de uma variável contínua. A altura de cada barra é proporcional à frequência da classe. A largura da barra é igual à largura da classe. A área de cada barra é proporcional à frequência da classe. A área total do histograma é igual ao número total de observações.¹⁰⁰

• Boxplots representam a distribuição de frequências de uma variável contínua. A linha central divide os dados em duas partes iguais (mediana ou Q2). A caixa inferior representa o primeiro quartil (Q1) e a caixa superior representa o terceiro quartil (Q3). A linha inferior é o mínimo e a linha superior é o máximo. Os valores atípicos são representados por pontos individuais.¹⁰⁰

O pacote grDevices¹⁰⁴ fornece a função nclass para determinar a quantidade de classes de um histograma com os métodos de Sturge¹⁰¹, Scott¹⁰² ou Freedman-Diaconis¹⁰³.

O pacote graphics¹⁰⁵ fornece a função hist para criar histogramas.

12.1.3 Quais características definem uma distribuição?

• Uma distribuição pode ser definida por modelos matemáticos e caracterizada por parâmetros de tendência central, dispersão, simetria e curtose.

12.1.4 Quais são as distribuições mais comuns?

• Distribuções discretas:

  • Uniforme: resultados (finitos) que são igualmente prováveis.^REF?

  • Binomial: número de sucessos em k tentativas.^REF?

  • Poisson: número de eventos em um intervalo de tempo fixo.^REF?

  • Bernoulli: .^REF?

  • Geométrica: número de testes até o 1o sucesso.^REF?

  • Binomial negativa: número de testes até o k-ésimo sucesso.^REF?

  • Hipergeométrica: número de indivíduos na amostra tomados sem reposição.^REF?

• Distribuições contínuas:

  • Uniforme: resultados que possuem a mesma densidade.^REF?

  • Exponencial: tempo entre eventos.^REF?

  • Normal: .^REF?

  • Normal padrão: .^REF?

  • Aproximação binomial: número de sucessos em uma grande quantidade de tentativas.^REF?

  • Aproximação Poisson: número de ocorrências em um intervalo de tempo fixo.^REF?

  • Qui-quadrado: .^REF?

  • t-Student: .^REF?

  • Weibull: .^REF?

  • Log-normal: .^REF?

  • Beta: .^REF?

  • Gama: .^REF?

  • Logística: .^REF?

  • Pareto.^REF?

12.1.5 Quais são as funções de uma distribuição?

• Função de massa de probabilidade (probability mass function, pmf).^REF?

• Função de distribuição cumulativa (cumulative distribution function, cdf).^REF?

• Função quantílicas (quantile function, qf).^REF?

• Função geradora de números aleatórios (random function, rf).^REF?

O pacote stats⁴⁴ fornece funções de distribuição de probabilidade (p), funções de densidade (d), funções quantílicas (q) e funções geradores de números aleatórios (r) para as distribuições normal, Student t, binomial, qui-quadrado, uniforme, dentre outras.

O pacote ggdist¹⁰⁶ fornece a função geom_slabinterval para criar gráficos de distribuição de probabilidade (p) e funções de densidade (d) as distribuições.

O pacote ggfortify¹⁰⁷ fornece a função ggdistribution para criar gráficos de distribuição de probabilidade (p), funções de densidade (d), funções quantílicas (q) e funções geradores de números aleatórios (r) para as distribuições.

12.1.6 O que é a distribuição normal?

• A distribuição normal (ou gaussiana) é uma distribuição com desvios simétricos positivos e negativos em torno de um valor central.⁷⁹

• Em uma distribuição normal, o intervalo de 1 desvio-padrão (±1DP) inclui cerca de 68% dos dados; de 2 desvios-padrão (±2DP) cerca de 95% dos dados; e no intervalo de 3 desvios-padrão (±3DP) cerca de 99% dos dados.⁷⁹

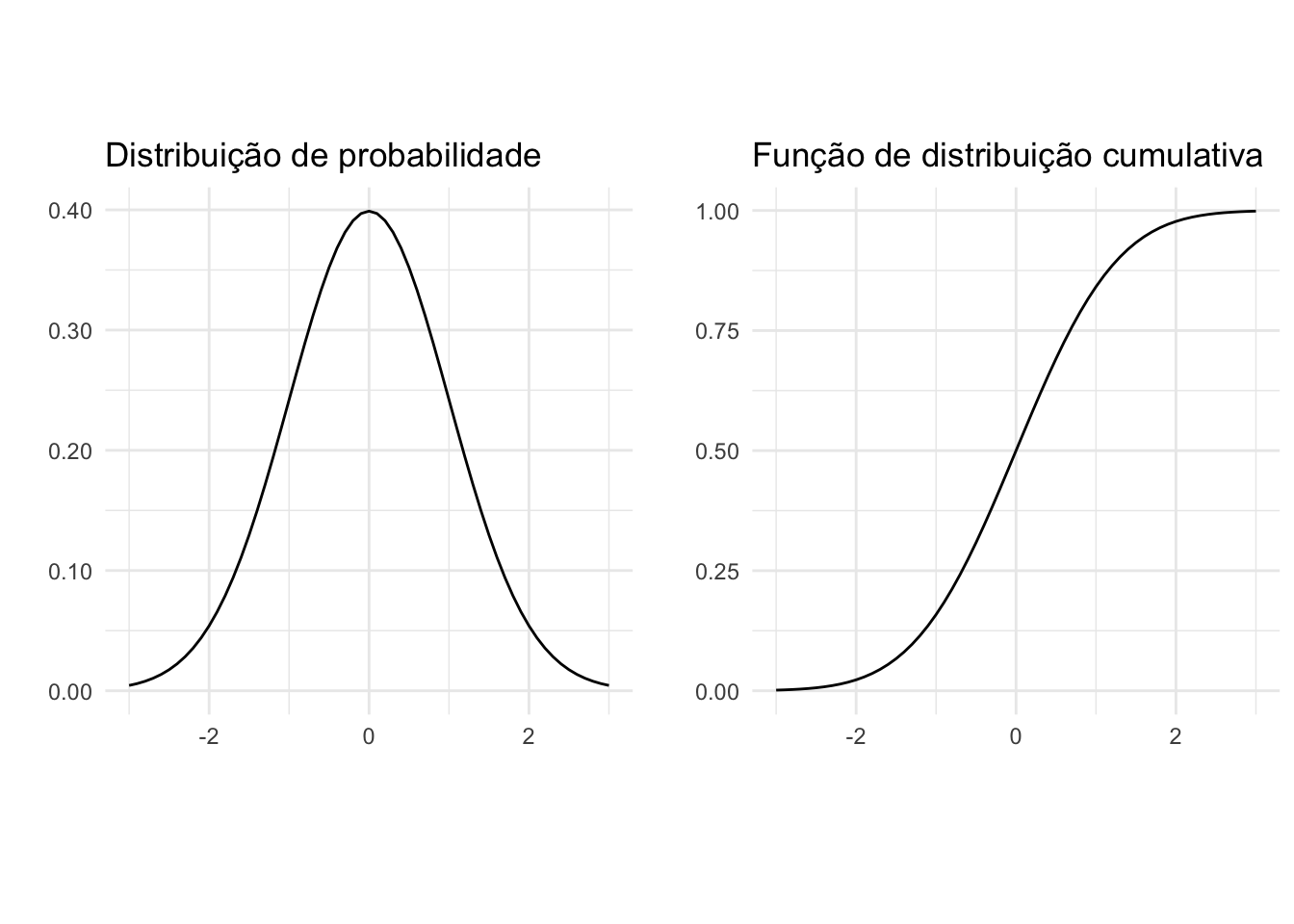
Figura 12.1: Distribuições e funções de probabilidade

12.1.7 Que métodos podem ser utilizados para identificar a normalidade da distribuição?

• Histogramas.⁴⁹

• Gráficos Q-Q.⁴⁹

• Testes de hipótese nula:⁴⁹

  • Kolmogorov-Smirnov

  • Shapiro-Wilk

  • Anderson-Darling

12.1.8 O que são distribuições não-normais?

• .^REF?

12.2 Parâmetros

12.2.1 O que são parâmetros?

• Parâmetros são informações que definem um modelo teórico, como propriedades de uma coleção de indivíduos.⁷⁸

• Parâmetros definem características de uma população inteira, tipicamente não observados por ser inviável ter acesso a todos os indivíduos que constituem tal população.⁴⁹

O pacote base⁵² fornece a função summary para calcular diversos parâmetros descritivos.

12.2.2 O que é uma análise paramétrica?

• Testes paramétricos possuem suposições sobre as características e/ou parâmetros da distribuição dos dados na população.⁴⁹

• Testes paramétricos assumem que: a variável é quantitativa numérica (contínua); os dados foram amostrados de uma população com distribuição normal; a variância da(S) amostra(s) é igual à da população; as amostras foram selecionadas de modo aleatório na população; os valores de cada amostra são independentes entre si.^49,79

• Testes paramétricos são baseados na suposição de que os dados amostrais provêm de uma população com parâmetros fixos determinando sua distribuição de probabilidade.⁸

12.2.3 O que é uma análise não paramétrica?

• Testes não-paramétricos fazem poucas suposições, ou menos rigorosas, sobre as características e/ou parâmetros da distribuição dos dados na população.^49,79

• Testes não-paramétricos são úteis quando as suposições de normalidade não podem ser sustentadas.⁷⁹

12.2.4 Devemos testar as suposições de normalidade?

• Testes preliminares de normalidade não são necessários para a maioria dos testes paramétricos de comparação, pois eles são robustos contra desvios moderados da normalidade. Normalidade da distribuição deve ser estabelecida para a população.¹⁰⁸

12.2.5 Por que as análises paramétricas são preferidas?

• Em geral, testes paramétricos são mais robustos (isto é, possuem menores erros tipo I e II) que seus testes não-paramétricos correspondentes.^49,109

• Testes não-paramétricos apresentam menor poder estatístico (maior erro tipo II) comparados aos testes paramétricos correspondentes.⁷⁹

12.2.6 Que parâmetros podem ser estimados?

• Parâmetros de tendência central.^79,110

• Parâmetros de dispersão.^79,110,111

• Parâmetros de proporção.^{79,110,112,112}

• Parâmetros de distribuição.¹¹⁰

• Parâmetros de extremos.⁷⁹

O pacote base⁵² fornece a função summary para calcular diversos parâmetros descritivos.

12.3 Tendência central

12.3.1 Que parâmetros de tendência central podem ser estimados?

• Média: aritmética, ponderada, geométrica ou harmônica.^79,110,113

• Mediana.^79,110,114

• Moda.^79,110,114

• A posição relativa das medidas de tendência central (média, mediana e moda) depende da forma da distribuição.¹¹⁴

• Em uma distribuição normal, as três medidas são idênticas.¹¹⁴

• A média é sempre puxada para os valores extremos, por isso é deslocada para a cauda em distribuições assimétricas.¹¹⁴

• A mediana fica entre a média e a moda em distribuições assimétricas.¹¹⁴

• A moda é o valor mais frequente e, portanto, se localiza no pico da distribuição assimétrica.¹¹⁴

O pacote base⁵² fornece a função summary para calcular diversos parâmetros descritivos.

12.3.2 Como escolher o parâmetro de tendência central?

• A mediana é preferida à média quando existem poucos valores extremos na distribuição, alguns valores são indeterminados, ou há uma distribuição aberta, ou os dados são medidos em uma escala ordinal.¹¹⁴

• A moda é preferida quando os dados são medidos em uma escala nominal.¹¹⁴

• A média geométrica é preferida quando os dados são medidos em uma escala logarítmica.¹¹⁴

12.4 Dispersão

12.4.1 Que parâmetros de dispersão podem ser estimados?

• Variância.^79,110

• Desvio-padrão: Informam sobre a dispersão da população e são, portanto, úteis como preditores da variação em novas amostras.^111,115,116

• Erro-padrão: Refletem a incerteza na média e sua dependência do tamanho da amostra.^111,115

• Amplitude.^79,110,116

• Intervalo interquartil.^79,110,116

• Intervalo de confiança: Captura a média populacional correspondente ao nível de significância \(\alpha\) pré-estabelecido.^{79,110,115,117}

O pacote base⁵² fornece a função summary para calcular diversos parâmetros descritivos.

O pacote stats⁴⁴ fornece a função confint para calcular o intervalo de confiança em um nível de significância \(\alpha\).

12.4.2 Como escolher o parâmetro de dispersão?

• Desvio-padrão é apropriado quando a média é utilizada como parâmetro de tendência central em distribuições simétricas.¹¹⁶

• Amplitue ou intervalo interquartil são apropriadas para variáveis ordinais ou distribuições assimétricas.¹¹⁶

12.5 Proporção

12.5.1 Que parâmetros de proporção podem ser estimados?

• Frequência absoluta.^79,110,112

• Frequência relativa.^79,110,112

• Percentil.^79,110,112

• Quantil: é o ponto de corte que define a divisão da amostra em grupos de tamanhos iguais. Portanto, não se referem aos grupos em si, mas aos valores que os dividem:¹¹²

  • Tercil: 2 valores que dividem a amostra em 3 grupos de tamanhos iguais.¹¹²

  • Quartil: 3 valores que dividem a amostra em 4 grupos de tamanhos iguais.¹¹²

  • Quintil: 4 valores que dividem a amostra em 5 grupos de tamanhos iguais.¹¹²

  • Decil: 9 valores que dividem a amostra em 10 grupos de tamanhos iguais.¹¹²

O pacote base⁵² fornece a função summary para calcular diversos parâmetros descritivos.

O pacote base⁵² fornece a função table para calcular proporções.

O pacote stats⁵² fornece a função quantile para executar análise de percentis.

12.6 Distribuição

12.6.1 Que parâmetros de distribuição podem ser estimados?

• Assimetria.¹¹⁰

• Curtose.¹¹⁰

12.7 Extremos

12.7.1 O que são extremos?

• Valores extremos podem constituir valores legítimos ou ilegítimos de uma distribuição.¹¹⁸

12.7.2 Que parâmetros extremos podem ser estimados?

• Mínimo.⁷⁹

• Máximo.⁷⁹

O pacote base⁵² fornece a função summary para calcular diversos parâmetros descritivos.

12.8 Valores discrepantes

12.8.1 O que são valores discrepantes (outliers)?

• Em termos gerais, um valor discrepante - “fora da curva” ou outlier - é uma observação que possui um valor relativamente grande ou pequeno em comparação com a maioria das observações.¹¹⁹

• Um valor discrepante é uma observação incomum que exerce influência indevida em uma análise.¹¹⁹

• Valores discrepantes são dados com valores altos de resíduos.¹¹⁸

12.8.2 Quais são os tipos de valores discrepantes?

• Valores discrepantes podem ser categorizados em três subtipos: outliers de erro, outliers interessantes e outliers aleatórios.¹¹⁸

• Os valores discrepantes de erro são observações claramente não legítimas, distantes de outros dados devido a imprecisões por erro de mensuração e/ou codificação.¹¹⁸

• Os valores discrepantes interessantes não são claramente erros, mas podem refletir um processo/mecanismo potencialmente interessante para futuras pesquisas.¹¹⁸

• Os valores discrepantes aleatórios são observações que resultam por acaso, sem qualquer padrão ou tendência conhecida.¹¹⁸

• Valores discrepantes podem ser univariados ou multivariados.¹¹⁸

12.8.3 Por que é importante avaliar valores discrepantes?

• Excluir o valor discrepante implica em reduzir inadequadamente a variância, ao remover um valor que de fato pertence à distribuição considerada.¹¹⁸

• Manter os dados inalterados (mantendo o valor discrepante) implica em aumentar inadequadamente a variância, pois a observação não pertence à distribuição que fundamenta o experimento.¹¹⁸

• Em ambos os casos, uma decisão errada pode influenciar o erro do tipo I (\(\alpha\) — rejeitar uma hipótese verdadeira) ou o erro do tipo II (\(\beta\) — não rejeitar uma hipótese falsa).¹¹⁸

12.8.4 Como detectar valores discrepantes?

• Na maioria das vezes, não há como saber de qual distribuição uma observação provém. Por isso, não é possível ter certeza se um valor é legítimo ou não dentro do contexto do experimento.¹¹⁸

• Recomenda-se seguir um procedimento em duas etapas: detectar possíveis candidatos a outliers usando ferramentas quantitativas; e gerenciar os outliers, decidindo manter, remover ou recodificar os valores, com base em informações qualitativas.¹¹⁸

• A detecção de outliers deve ser aplicada apenas uma vez no conjunto de dados; um erro comum é identificar e tratar os outliers (como remover ou recodificar) e, em seguida, reaplicar o procedimento no conjunto de dados já modificado.¹¹⁸

• A detecção ou o tratamento dos outliers não deve ser realizada após a análise dos resultados, pois isso introduz viés nos resultados.¹¹⁸

12.8.5 Quais são os métodos para detectar valores discrepantes?

• Valores univariados são comumente considerados outliers quando são mais extremos do que a média ± (desvio padrão × constante), podenso essa constante ser 3 (99,7% das observações estão dentro de 3 desvios-padrão da média) ou 3,29 (99,9% estão dentro de 3,29 desvios-padrão).¹¹⁸

• Para detectar outliers univariados, recomenda-se o uso da Mediana da Desviação Absoluta (Median Absolute Deviation, MAD), calculado a partir de um intervalo em torno da mediana, multiplicado por uma constante (valor padrão: 1,4826).^118,120

• Para detectar outliers multivariados, comumente utiliza-se a distância de Mahalanobis, que identifica valores muito distantes do centróide formado pela maioria dos dados (por exemplo, 99%).¹¹⁸

• Para detectar outliers multivariados, recomenda-se o Determinante de Mínima Covariância (Minimum Covariance Determinant, MCD), pois possui o maior ponto de quebra possível e utiliza a mediana, que é o indicador mais robusto em presença de outliers.^118,121

12.8.6 Como manejar os valores discrepantes?

• Manter outliers pode ser uma boa decisão se a maioria desses valores realmente pertence à distribuição de interesse. Manter outliers que pertencem a uma distribuição alternativa pode ser problemático, pois um teste pode se tornar significativo apenas por causa de um ou poucos outliers.¹¹⁸

• Remover outliers pode ser eficaz quando eles distorcem a estimativa dos parâmetros da distribuição. Remover outliers que pertencem legitimamente à distribuição pode reduzir artificialmente a estimativa do erro.¹¹⁸

• Remover outliers leva à perda de observações, especialmente em conjuntos de dados com muitas variáveis, quando outliers univariados são excluídos em cada variável.¹¹⁸

• Recodificar outliers evita a perda de uma grande quantidade de dados, mas deve ser baseada em argumentos razoáveis e convincentes.¹¹⁸

• Erros de observação e de medição são uma justificativa válida para descartar observações discrepantes.¹¹⁹

12.8.7 Como conduzir análises com valores discrepantes?

• É importante reportar se existem valores discrepantes e como foram tratados.¹¹⁹

• Valores discrepantes na variável de desfecho podem exigir uma abordagem mais refinada, especialmente quando representam uma variação real na variável que está sendo medida.¹¹⁹

• Valores discrepantes em uma (co)variável podem surgir devido a um projeto experimental inadequado; nesse caso, abandonar a observação ou transformar a covariável são opções adequadas.¹¹⁹

• Valores discrepantes podem ser recodificados usando a Winsorização,¹²² que transforma os outliers em valores de percentis específicos (como o 5º e o 95º).¹¹⁸

O pacote outliers¹²³ fornece a função outlier para identificar os valores mais distantes da média.

O pacote outliers¹²³ fornece a função rm.outlier para remover os valores mais distantes da média detectados por testes de hipótese e/ou substitui-los pela média ou mediana.

Referências

8.

Kwak SG, Kim JH. Central limit theorem: the cornerstone of modern statistics. Korean Journal of Anesthesiology. 2017;70(2):144. doi:10.4097/kjae.2017.70.2.144

44.

R Core Team. R: A Language and Environment for Statistical Computing.; 2023. https://www.R-project.org/.

49.

Vetter TR. Fundamentals of Research Data and Variables. Anesthesia & Analgesia. 2017;125(4):1375-1380. doi:10.1213/ane.0000000000002370

52.

R Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2023. https://www.R-project.org/.

78.

Altman DG, Bland JM. Statistics notes Variables and parameters. BMJ. 1999;318(7199):1667-1667. doi:10.1136/bmj.318.7199.1667

79.

Ali Z, Bhaskar Sb. Basic statistical tools in research and data analysis. Indian Journal of Anaesthesia. 2016;60(9):662. doi:10.4103/0019-5049.190623

100.

S M. Frequency distribution. Journal of Pharmacology and Pharmacotherapeutics. 2011;2(1):54-56. doi:10.4103/0976-500x.77120

101.

Sturges HA. The Choice of a Class Interval. Journal of the American Statistical Association. 1926;21(153):65-66. doi:10.1080/01621459.1926.10502161

102.

SCOTT DW. On optimal and data-based histograms. Biometrika. 1979;66(3):605-610. doi:10.1093/biomet/66.3.605

103.

Freedman D, Diaconis P. On the histogram as a density estimator:L 2 theory. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete. 1981;57(4):453-476. doi:10.1007/bf01025868

104.

R Core Team. R: A language and environment for statistical computing. 2024. https://www.R-project.org/.

105.

R Core Team. R: A language and environment for statistical computing. 2023. https://www.R-project.org/.

106.

Kay M. Ggdist: Visualizations of distributions and uncertainty in the grammar of graphics. 2024;30. doi:10.1109/TVCG.2023.3327195

107.

Tang Y, Horikoshi M, Li W. Ggfortify: Unified Interface to Visualize Statistical Result of Popular r Packages. Vol 8.; 2016. doi:10.32614/RJ-2016-060

108.

Rochon J, Gondan M, Kieser M. To test or not to test: Preliminary assessment of normality when comparing two independent samples. BMC Medical Research Methodology. 2012;12(1). doi:10.1186/1471-2288-12-81

109.

Greenhalgh T. How to read a paper: Statistics for the non-statistician. I: Different types of data need different statistical tests. BMJ. 1997;315(7104):364-366. doi:10.1136/bmj.315.7104.364

110.

Kanji G. 100 Statistical Tests.; 2006. doi:10.4135/9781849208499

111.

Curran-Everett D. Explorations in statistics: standard deviations and standard errors. Advances in Physiology Education. 2008;32(3):203-208. doi:10.1152/advan.90123.2008

112.

Altman DG, Bland JM. Statistics Notes: Quartiles, quintiles, centiles, and other quantiles. BMJ. 1994;309(6960):996-996. doi:10.1136/bmj.309.6960.996

113.

S. M. Measures of central tendency: The mean. Journal of Pharmacology and Pharmacotherapeutics. 2011;2(2):140-142. doi:10.4103/0976-500x.81920

114.

S. M. Measures of central tendency: Median and mode. Journal of Pharmacology and Pharmacotherapeutics. 2011;2(3):214-215. doi:10.4103/0976-500x.83300

115.

Krzywinski M, Altman N. Error bars. Nature Methods. 2013;10(10):921-922. doi:10.1038/nmeth.2659

116.

Manikandan S. Measures of dispersion. Journal of Pharmacology and Pharmacotherapeutics. 2011;2(4):315-316. doi:10.4103/0976-500x.85931

117.

Cumming G, Fidler F, Vaux DL. Error bars in experimental biology. The Journal of Cell Biology. 2007;177(1):7-11. doi:10.1083/jcb.200611141

118.

Leys C, Delacre M, Mora YL, Lakens D, Ley C. How to Classify, Detect, and Manage Univariate and Multivariate Outliers, With Emphasis on Pre-Registration. International Review of Social Psychology. 2019;32(1). doi:10.5334/irsp.289

119.

Zuur AF, Ieno EN, Elphick CS. A protocol for data exploration to avoid common statistical problems. Methods in Ecology and Evolution. 2009;1(1):3-14. doi:10.1111/j.2041-210x.2009.00001.x

120.

Leys C, Ley C, Klein O, Bernard P, Licata L. Detecting outliers: Do not use standard deviation around the mean, use absolute deviation around the median. Journal of Experimental Social Psychology. 2013;49(4):764-766. doi:10.1016/j.jesp.2013.03.013

121.

Leys C, Klein O, Dominicy Y, Ley C. Detecting multivariate outliers: Use a robust variant of the Mahalanobis distance. Journal of Experimental Social Psychology. 2018;74:150-156. doi:10.1016/j.jesp.2017.09.011

122.

Tukey JW, McLaughlin DH. Less vulnerable confidence and significance procedures for location based on a single sample: Trimming/winsorization 1. Sankhyā: The Indian Journal of Statistics, Series A (1961-2002). 1963;25(3):331-352. http://www.jstor.org/stable/25049278. Accessed April 11, 2025.

123.

Komsta L. Outliers: Tests for Outliers.; 2022. https://CRAN.R-project.org/package=outliers.