Capítulo 31 Regressão
31.1 Análise de regressão
31.1.1 O que é regressão?
Regressão refere-se a uma equação matemática que permite que uma ou mais variável(is) de desfecho (dependentes) seja(m) prevista(s) a partir de uma ou mais variável(is) independente(s). A regressão implica em uma direção de efeito, mas não garante causalidade.171
Para estimar os efeitos imparciais de um fator de exposição primária sobre uma variável de desfecho, frequentemente constroem-se modelos estatísticos de regressão.150
O pacote modelsummary247 fornece as funções modelsummary e modelplot para gerar tabelas e gráficos de coeficientes de regressão.
O pacote gtsummary145 fornece a função tbl_regression para construção da ‘Tabela 2’ com dados do modelo de regressão.
31.1.3 O que são análises de regressão simples?
- A análise de regressão simples consiste em modelos estatísticos com 1 variável dependente (desfecho) e 1 variável independente (preditor).248
31.1.4 O que são análises de regressão multivariável?
- A análise multivariável (ou múltiplo) consiste em modelos estatísticos com 1 variável dependente (desfecho) e duas ou mais variáveis independentes.248
31.1.5 O que são análises de regressão multivariada?
- A análise multivariada consiste em modelos estatísticos com 2 ou mais variáveis dependente (desfechos) e duas ou mais variáveis independentes.248
31.2 Preparação de variáveis para regressão
31.2.1 Como preparar as variáveis categóricas para análise de regressão?
Variáveis fictícias (dummy) compreendem variáveis criadas para introduzir, nos modelos de regressão, informações contidas em outras variáveis que não podem ser medidas em escala numérica.249
Variáveis categóricas nominais, com 2 ou mais níveis, devem ser subdivididas em variáveis fictícias dicotômicas para ser usada em modelos de regressão.250
Cada nível da variável categórica nominal será convertido em uma nova variável fictícias dicotômica, tal que a nova variável dicotômica assume valor 1 para a presença do nível correspondente e 0 em qualquer outro caso.250
O pacote fastDummies251 fornece a função dummy_cols para preparar as variáveis categóricas fictícias para análise de regressão.
31.3 Redução de dimensionalidade para regressão
31.3.1 Correlação bivariada pode ser usada para seleção de variáveis em modelos de regressão multivariável?
Seleção bivariada de variáveis - isto é, aplicação de testes de correlação em pares de variáveis candidatas e variável de desfecho afim de selecionar quais serão incluídas no modelo multivariável - é um dos erros mais comuns na literatura.196,252,253
A seleção bivariada de variáveis torna o modelo mais suscetível a otimismo no ajuste se as variáveis de confundimento não são adequadamente controladas.252,253
31.3.2 Variáveis sem significância estatística devem ser excluídas do modelo final?
Eliminar uma variável de um modelo significa anular o seu coeficiente de regressão (\(\beta = 0\)), mesmo que o valor estimado pelos dados seja outro. Desta forma, os resultados se afasTAM de uma solução de máxima verossimilhança (que tem fundamento teórico) e o modelo resultante é intencionalmente subótimo.196
Os coeficientes de regressão geralmente dependem do conjunto de variáveis do modelo e, portanto, podem mudam de valor (“mudança na estimativa” positiva ou negativa) se uma (ou mais) variável(is) for(em) eliminada(s) do modelo.196
31.3.3 Por que métodos de regressão gradual não são recomendados para seleção de variáveis em modelos de regressão multivariável?
Métodos diferentes de regressão gradual podem produzir diferentes seleções de variáveis de um mesmo banco de dados.250
Nenhum método de regressão gradual garante a seleção ótima de variáveis de um banco de dados.250
As regras de término da regressão baseadas em P-valor tendem a ser arbitrárias.250
31.3.4 O que pode ser feito para reduzir o número de variáveis candidatas em modelos de regressão multivariável?
- Verifique a existência de multicolinearidade entre as variáveis candidatas.253
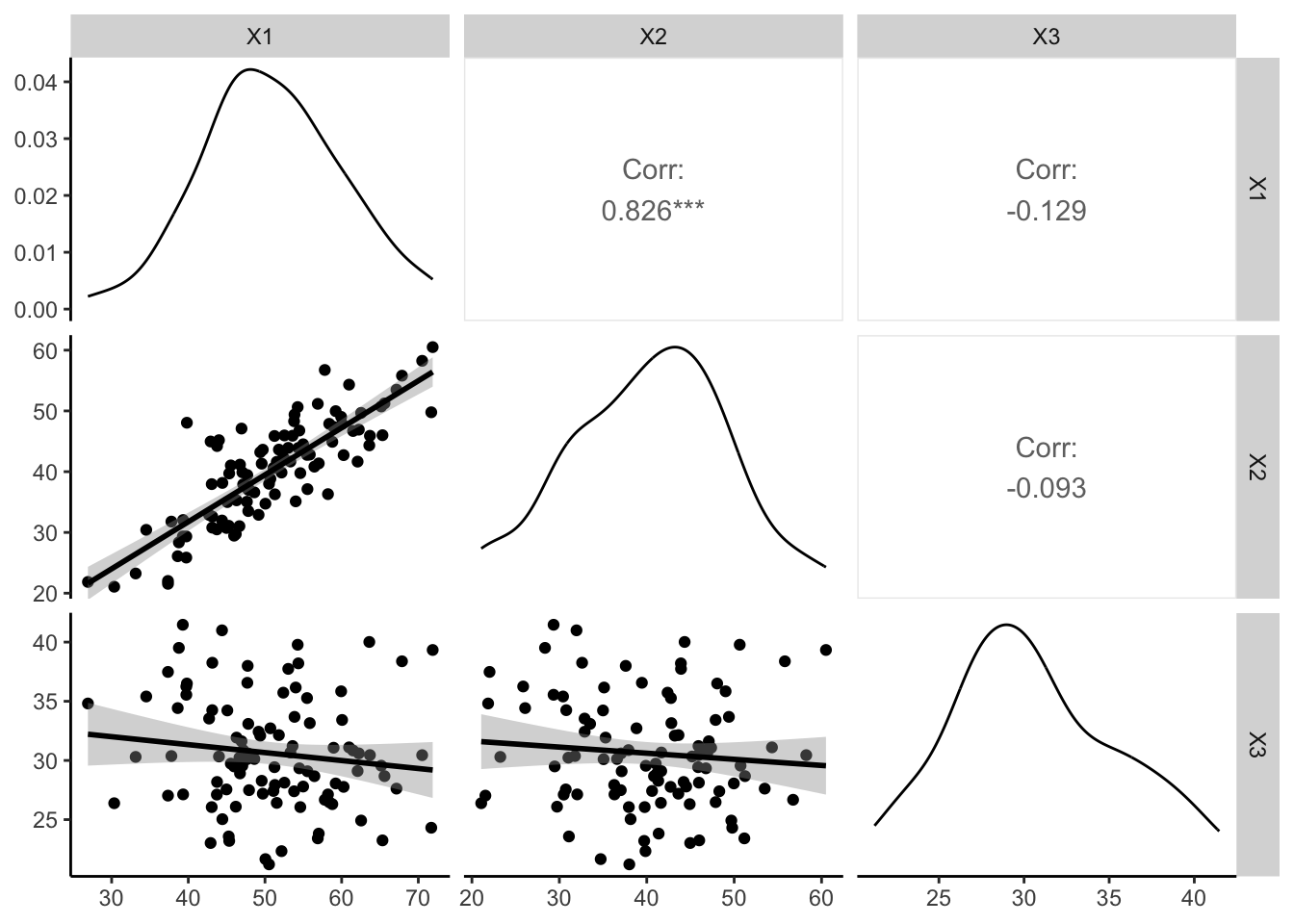
Figura 31.1: Multicolinearidade entre variáveis candidatas em modelos de regressão multivariável.
Em caso de uma proporção baixa entre o número de participantes e de variáveis, use o conhecimento prévio da literatura para selecionar um pequeno conjunto de variáveis candidatas.253
Colapse categorias com contagem nula (células com valor igual a 0) de variáveis candidatas.253
Use simulações de dados para identificar qual(is) variável(is) está(ão) causando problemas de convergência do ajuste do modelo.253
A eliminação retroativa tem sido recomendada como a abordagem de regressão gradual mais confiável entre aquelas que podem ser facilmente alcançadas com programas de computador.196