Capítulo 4 Paradoxos e falácias
4.1 Paradoxos estatísticos
4.1.1 O que são paradoxos estatísticos?
- Paradoxos podem originar da incompreensão ou mal informação da nossa intuição a respeito do fenômeno.24
4.1.4 O que é o paradoxo de Big Data?
- “Quanto maior a quantidade de dados, maior a certeza de que vamos nos enganar”.24
4.1.11 O que é o paradoxo de Simpson?
O paradoxo de Simpson ocorre quando a associação entre duas variáveis \(X\) e \(Y\) desaparece ou mesmo reverte sua direção quando condicionadas em uma terceira variável \(Z\).34,35
Para decisão do paradoxo de Simpson pode-se utilizar o conceito de ‘back-door’, o qual considera os ‘caminhos’ (isto é, associações) no gráfico acíclio direcionado e assegura que todos as associações espúrias do tratamento \(X\) para o desfecho \(Y\) nesse diagrama causal sejam interceptados pela variável \(Z\).36
Dependendo do contexto em que os dados foram obtidos — delineamento do estudo, escolha dos instrumentos e dos tipos de variáveis — a melhor escolha para a análise pode variar entre a análise da população agregada ou da subpopulação desagregada.36
É possivel que em alguns contextos nem a análise agregada ou a desagregada podem oferecer a resposta correta, sendo necessário o uso de outras (mais) covariáveis.36
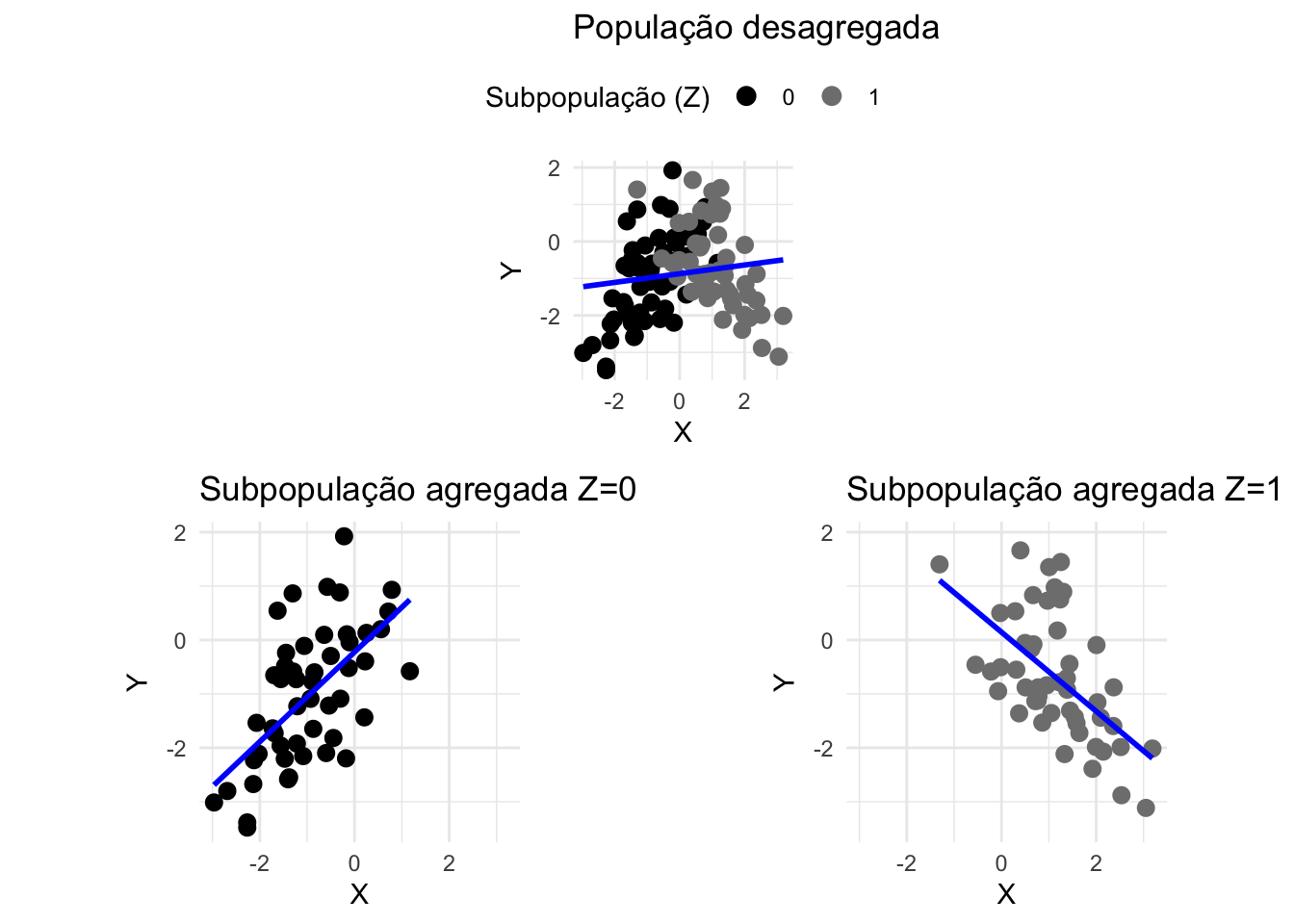
Figura 4.1: Paradoxo de Simpson representado com dados simulados. Os pontos no gráfico representam observações individuais e as linhas de tendência representam as regressões lineares ajustadas para os dados desagregados da população e agregados por subpopulação.
4.2 Falácias estatísticas
4.2.1 O que são falácias estatísticas?
Falácias estatísticas são erros de raciocínio que ocorrem em situações que envolvem dados e estatísticas. Elas podem ocorrer em qualquer etapa do processo de análise de dados, desde a coleta até a interpretação dos resultados.Elas podem ser intencionais ou não intencionais, e podem ser usadas para manipular, enganar ou confundir as pessoas.REF?
As falácias estatísticas podem ser difíceis de detectar, pois muitas vezes são sutis e podem parecer plausíveis à primeira vista. No entanto, é importante estar ciente delas e saber como identificá-las para evitar erros de interpretação e tomada de decisão.REF?
4.2.2 O que é a falácia do jogador?
- A falácia do jogador é a crença de que eventos independentes têm uma influência sobre eventos futuros. Por exemplo, se uma moeda é lançada várias vezes e cai cara em todas as vezes, a falácia do jogador sugere que a próxima jogada será coroa, pois a moeda “deve” se equilibrar. No entanto, cada lançamento da moeda é independente e não afeta o resultado do próximo lançamento.40
4.2.3 O que é a falácia da mão quente?
- A falácia da mão quente é a crença de que um jogador que teve sucesso em um jogo de azar terá mais chances de sucesso no futuro. Por exemplo, se uma moeda é lançada várias vezes e cai cara em todas as vezes, a falácia da mão quente sugere que a próxima jogada será cara, pois o jogador está “quente”. No entanto, cada lançamento da moeda é independente e não afeta o resultado do próximo lançamento.40